题目
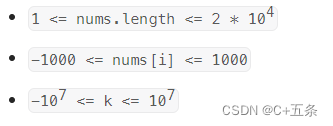
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。
子数组是数组中元素的连续非空序列。
示例 1:
输入:nums = [1,1,1], k = 2 输出:2
示例 2:
输入:nums = [1,2,3], k = 3 输出:2
思路
因为这道题刚开始确实被刺了博主一把,所以有感而发下面多啰嗦两句警示大家。
仔细观察题目可以发现,表面人畜无害的题目背地里却暗藏杀机,博主在看到题目的第一瞬间扫描到 子数组 和为k 看了两个示例 顿时大喜,直接上手以迅雷不及掩耳之势敲出滑动窗口解法,试图直接通过left与right两员大将拿下此题,不出意外的话果然出意外了,在再次看到数据范围后果断将两位大将收回。另寻他法。
这里解释一下,滑动窗口是在题目所给数据具有单调性时,通过准确的把握单调性来减少遍历或枚举的次数从而达到降低时间复杂度的目的,而本题数据有正有负,且为乱序排列,我们无法准确把握每组数据的单调性,所以无法使用滑动窗口来进行解题。
而结合求和,子数组,和样例等种种特点排除滑动窗口后,前缀和无疑时此时最适合的方式。
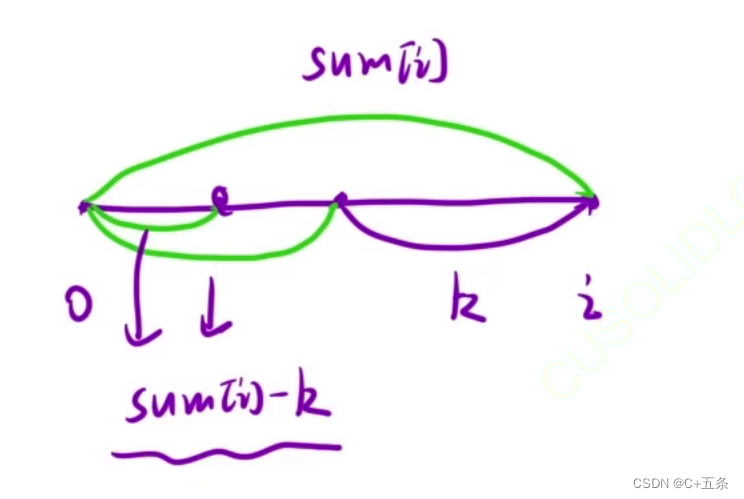
可是涉及到子序列的问题,即使直接求出前缀和数组,如果进行简单的遍历再去一个个计算,那么复杂度直逼O(n^2),加上构造前缀和数组,复杂度还不如直接暴力枚举。所以需要在前缀和基础上进行优化,题目让求有多少个子集,那可以抽象为第i个结点之前有多少个符合和为k的结点,然后一个节点一个节点去求,从而可以再抽象为,第i个位置之前,有多少个节点等于第i个节点的前缀和-k。及判断在[0,i-1]区间内有多少个前缀和等于sum[i]-k;
因为数据没有单调性,所以i之前可能出现多个子串符合条件,而每次查找会消耗掉多余的时间,所以直接创建一个哈希表,对应进行查找,每次先查找再插入当前节点
注意:[0,i-1]==sum[i]-k,判断是否存在可以分为以下情况:
1、从0加到 i 在nums数组中的那位刚好等于k,那sum[i]-k就是0;此时需要到0,-1区间去找,所以直接将哈希表0位置初始化成1,当这种情况出现时直接加上。
2、从0到i中间j位置的和刚好为sum[i]-k,那么从j+1到i的值就是k,符合情况。
3、i位置为k,那[0,i-1]就是sum[i]-k;
代码实现
class Solution { public: int subarraySum(vector<int>& nums, int k) { unordered_map<int,int> hash; hash[0]=1; int sum=0,ret=0; for(auto &x:nums) { sum+=x; if(hash.count(sum-k)) ret+=hash[sum-k]; hash[sum]++; } return ret; } };