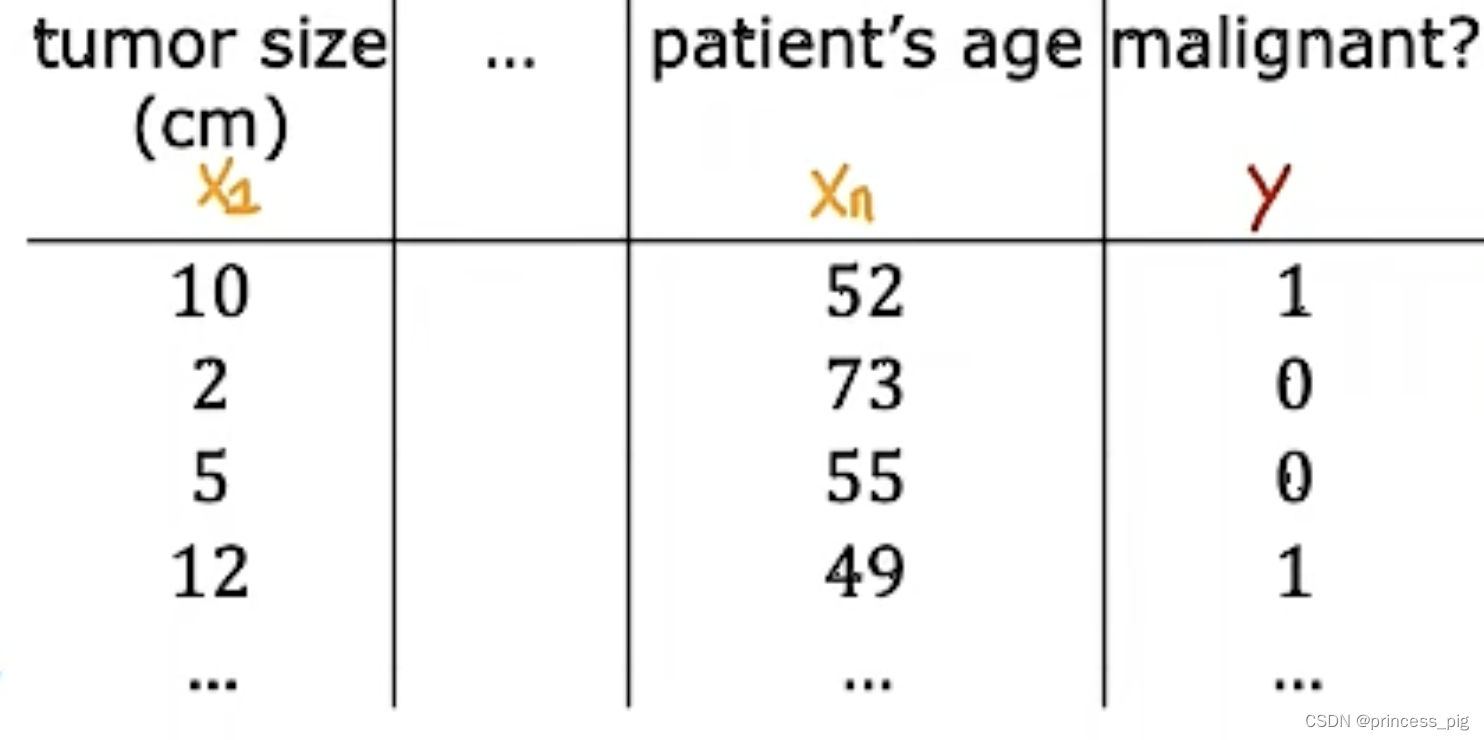
逻辑回归(logical regression):
逻辑回归这个名字听上去好像应该是回归算法的,但其实这个名字只是在历史上取名有点区别,但实际上它是一个完全属于是分类算法的。
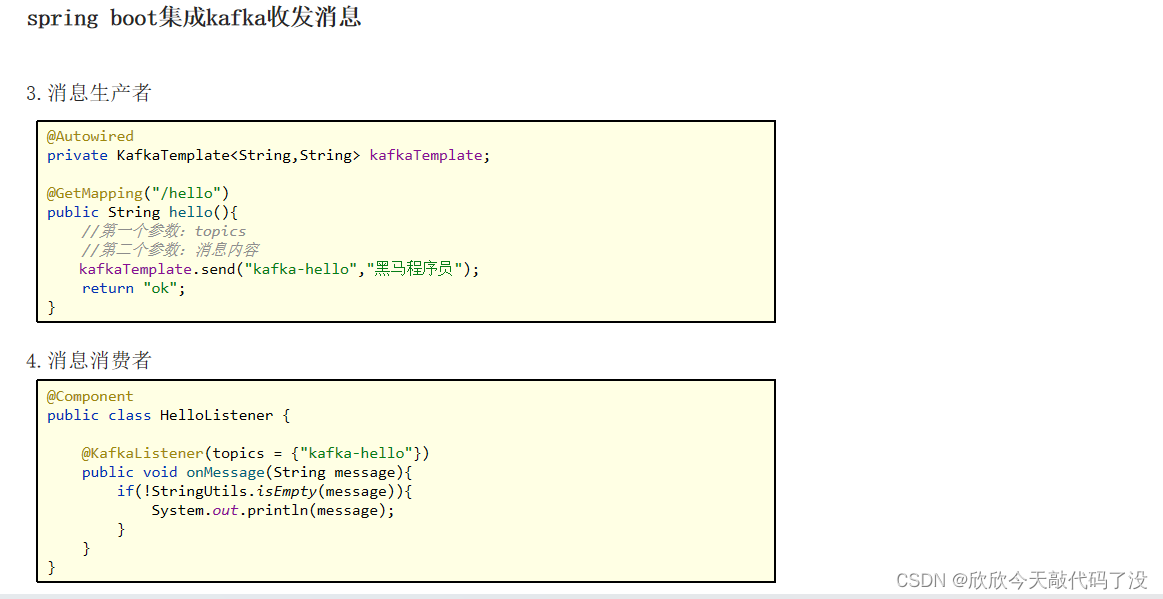
我们为什么要学习它呢?在用我们的线性回归时会遇到一个很大的问题,就比如一下的图形。
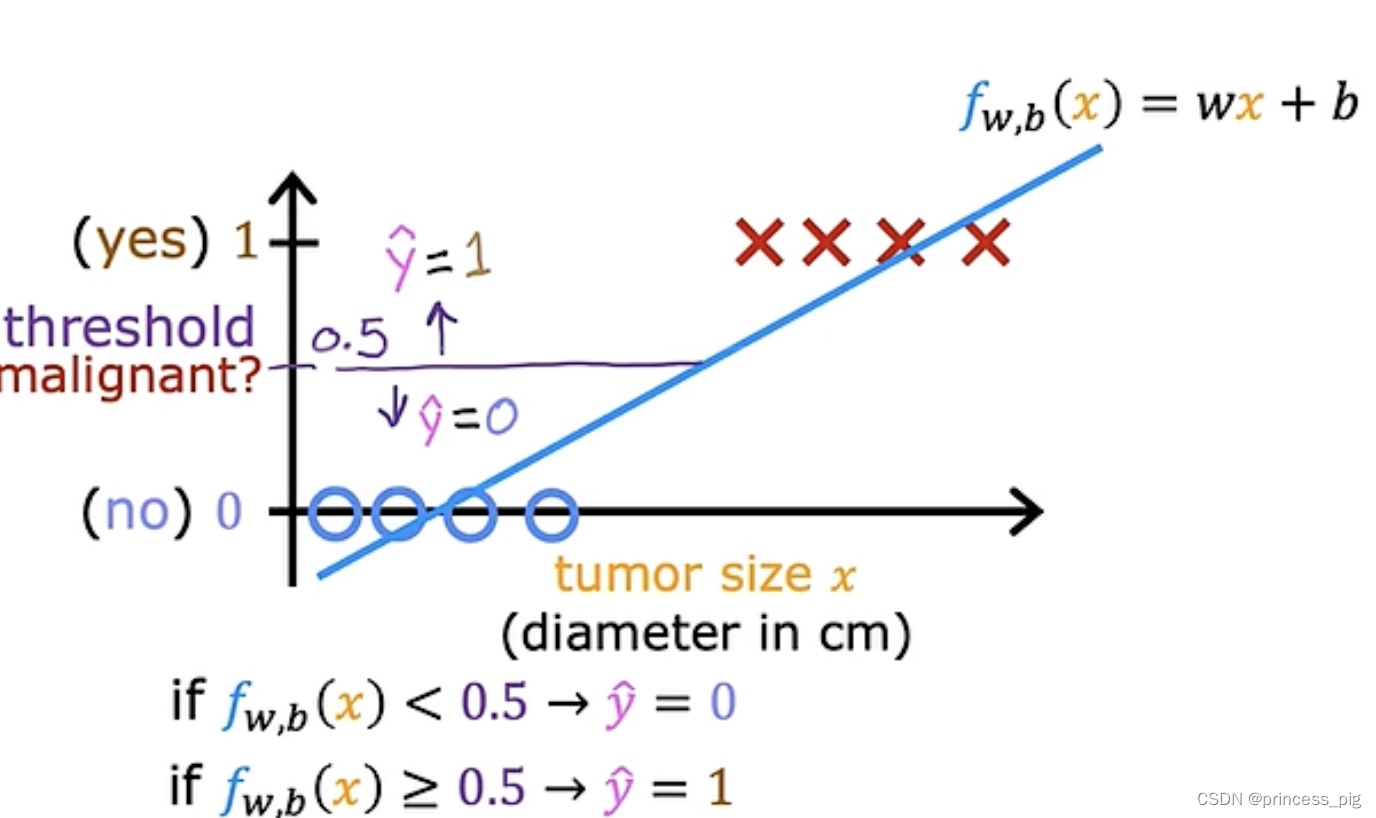
在这里我们把以上的图形进行了我们的线性回归得到了在0.5纵坐标的分界线,在0.5左侧是我们的良性肿瘤而在右边是我们的恶性肿瘤,这时我们得到了我们判断是否是良性肿瘤的方法,但当我们再添加一个数据时。
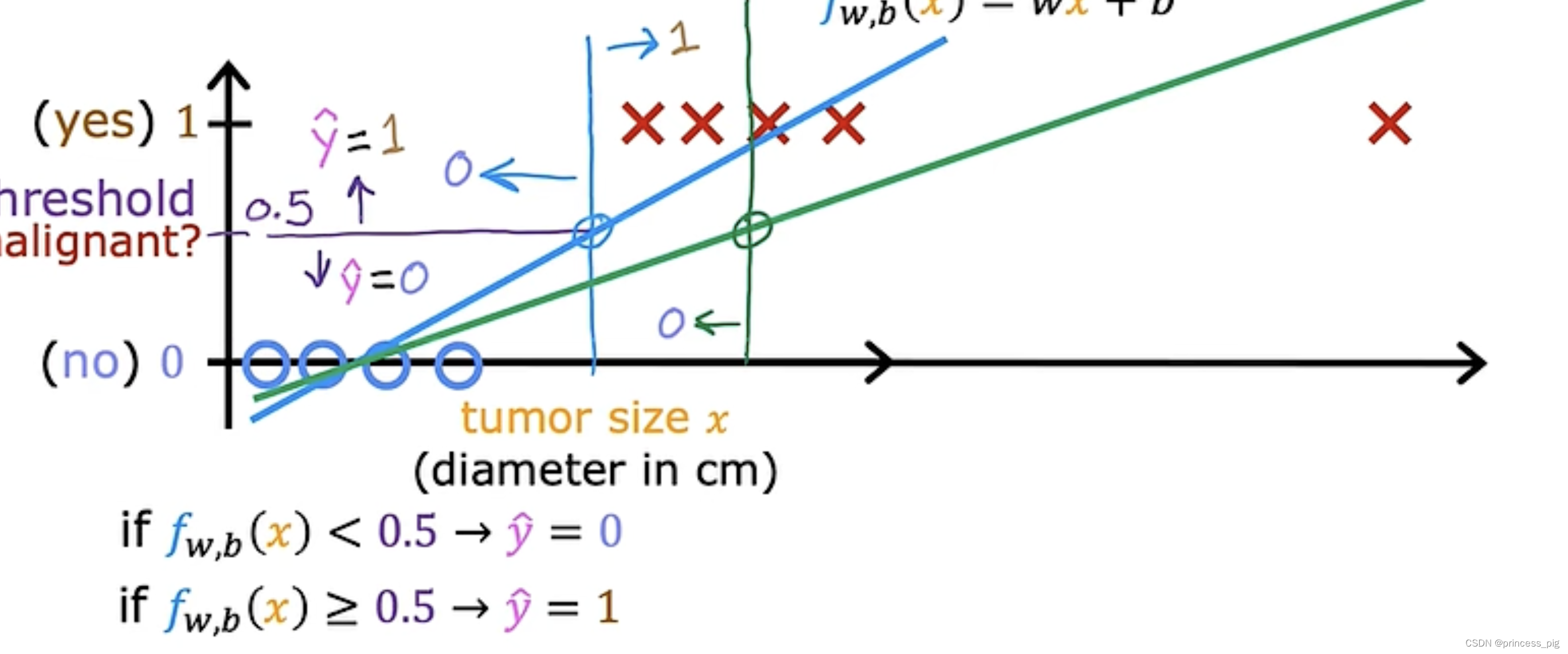
我们会发现我们的线性回归往右边平移了,而判断是否为良性肿瘤的值也往右边移动了,这时我们的模型就会因为我们的数据而发生变化,这很明显不是一个准确的方法,让我们得到我们需要的数据。所以我们需要学习一种叫做逻辑回归的算法。
逻辑函数(sigmoid function)
所以我们要创建一种新的函数。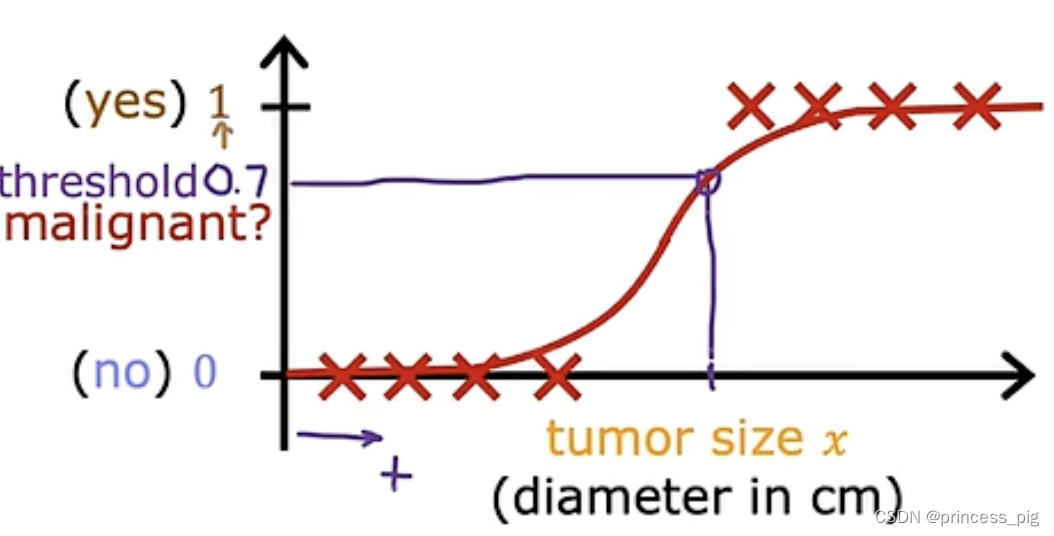
这里我们使用了sigmoid函数, 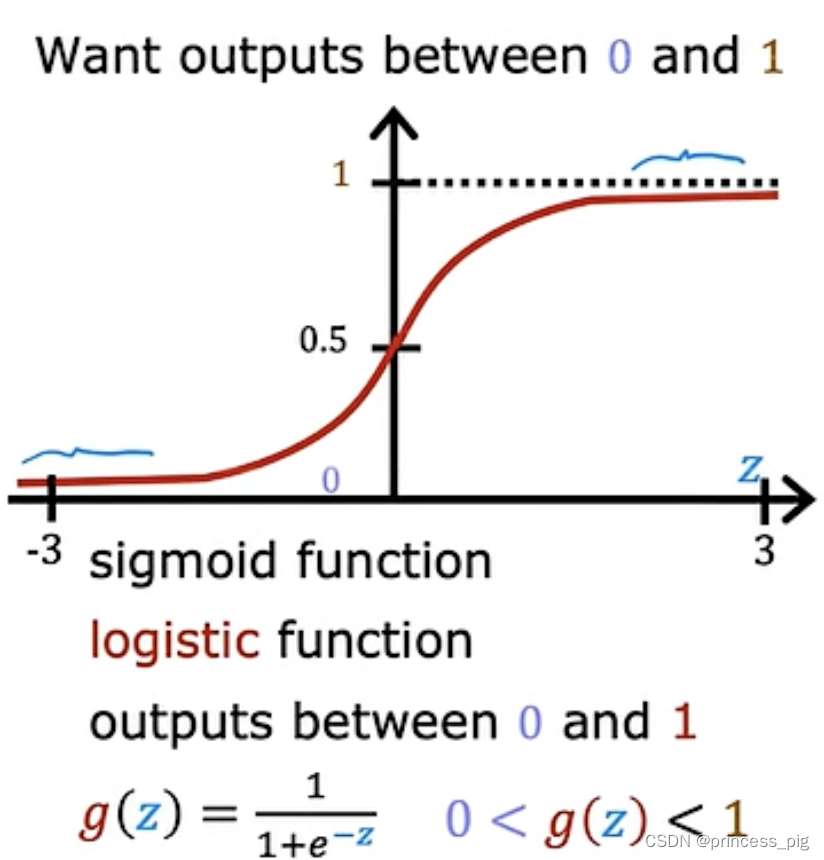
可以看到我们这个函数,,它所得到的函数可以是我们上图所示的样子。(可以自己手动画一下)在无限接近正无穷的地方它还是在缓慢的上升,而在负无穷处它则是无限接近于0。
那我们如何才能写一个逻辑回归函数呢?
第一步:我们的回归函数是,它的具体写法是
.。
第二步:我们sigmoid函数是。
第三步:我们把第一个式子代入,也就变成了。
我们解释一下我们得到的函数,在原来函数中我们知道它的y值在0到1,所以我们输入的x总会得到我们的一个值,而这个值一定在0和1之间,举一个例子。就那我们的判断肿瘤是否是恶性的例子,当我们的值为1时,则肿瘤为恶性肿瘤,当我们的值为0时,则它为良性肿瘤,当我们代入一个值时,y值输出为0.7,那么它就表示你有70%的概率会是恶性肿瘤。那为良性肿瘤的概率则为我们的30%。
这里有几个写法需要我们注意:1.,它指的是我们为1和为0的概率加起来为100%。2.
,它代表的意思就是我们的y=1时,我们的概率,而这里的w,b他们代表的只是它们对我们的答案会造成影响。
决策边界(Decision Boundary):
简单来说我们的决策边界就是当我们的逻辑函数曲线,在y值等于0.5时,也就是我们的z=0时,我们可以看看这个图。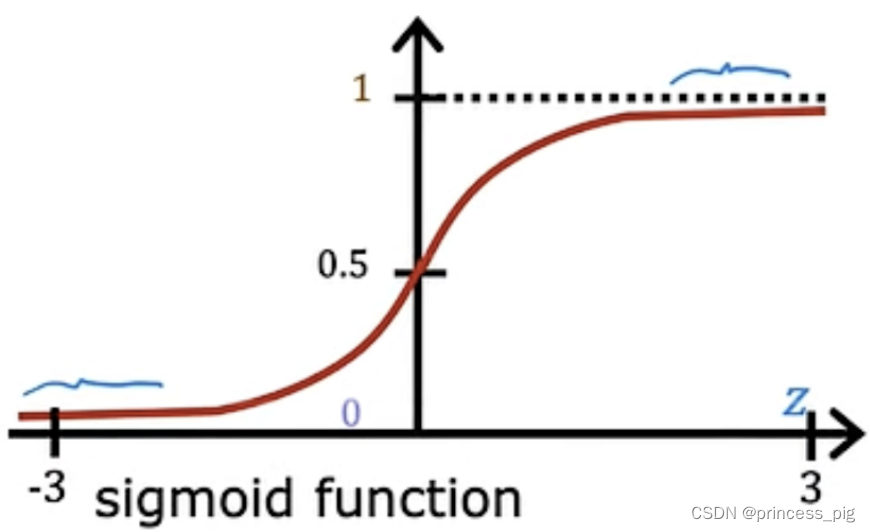
也就是 。我们举一个例子。比如得到了以下的图形。
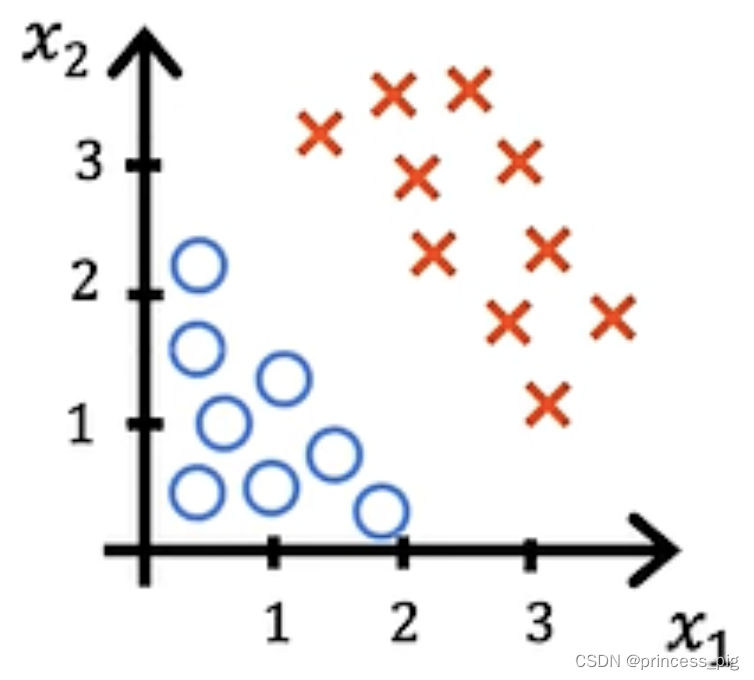 在图中我们的❌指的是我们的好的事物,而⭕️指的是坏的事物,这时,我们要找到我们的决策分界线。
在图中我们的❌指的是我们的好的事物,而⭕️指的是坏的事物,这时,我们要找到我们的决策分界线。
我们得到的数据是,这时我们假设我们的w1=1,w2=1,b=-3。这时我们得到的决策函数也就是
,这时我们就可以画出完美的决策边界。
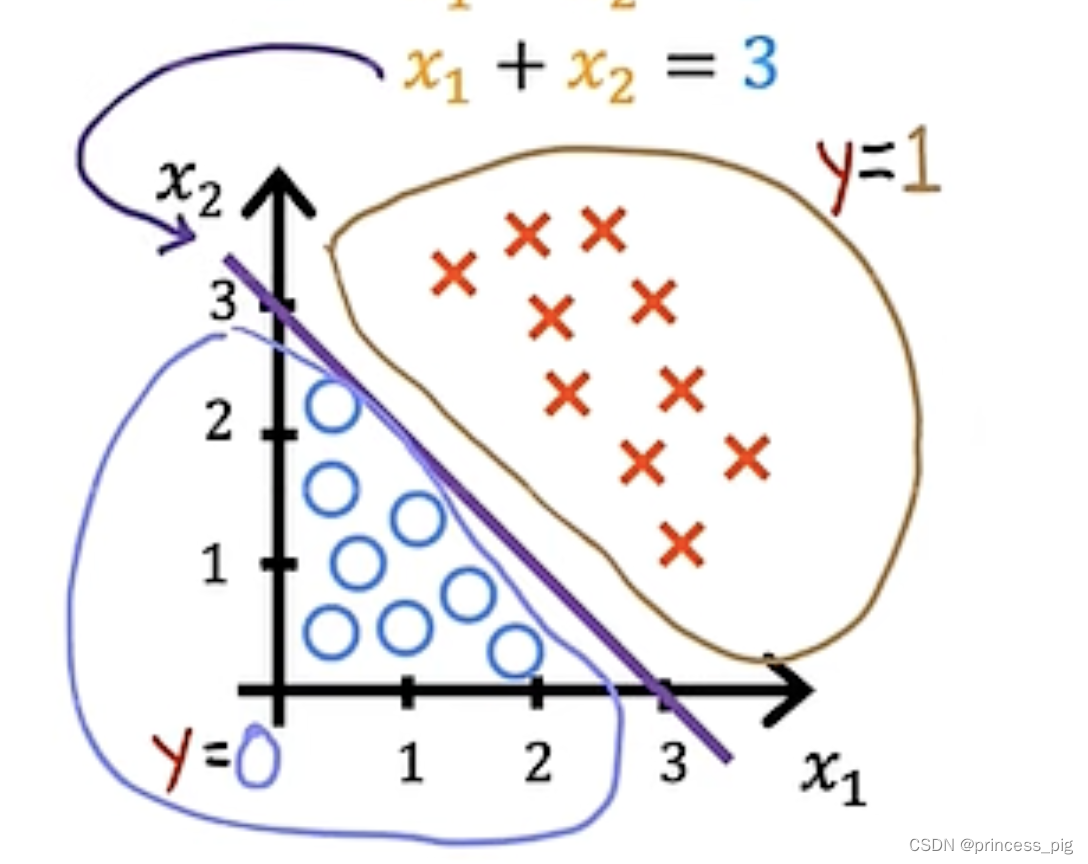
在上面就是我们的好事物,下面就是坏事物。这里有一个要强调,我们一般把0.5以上的看作是1,把0.5以下的看作成0。
当然也有多项式的情况,比如下图。
逻辑函数的成本函数(cost function):
在这个例子里面,我们的判断是否是一个良性肿瘤需要多组训练集,这里在前面几个特征与线性回归类似,而最后一个判断是否是良性或恶性用的是1和0来表示。
我们用原来的线性回归中,使用的成本函数,我们得到的图形将是。凹凸不平的,这让我们用梯度下降时只能取到我们的局部最小值,而不能得到我们的全局最小值。
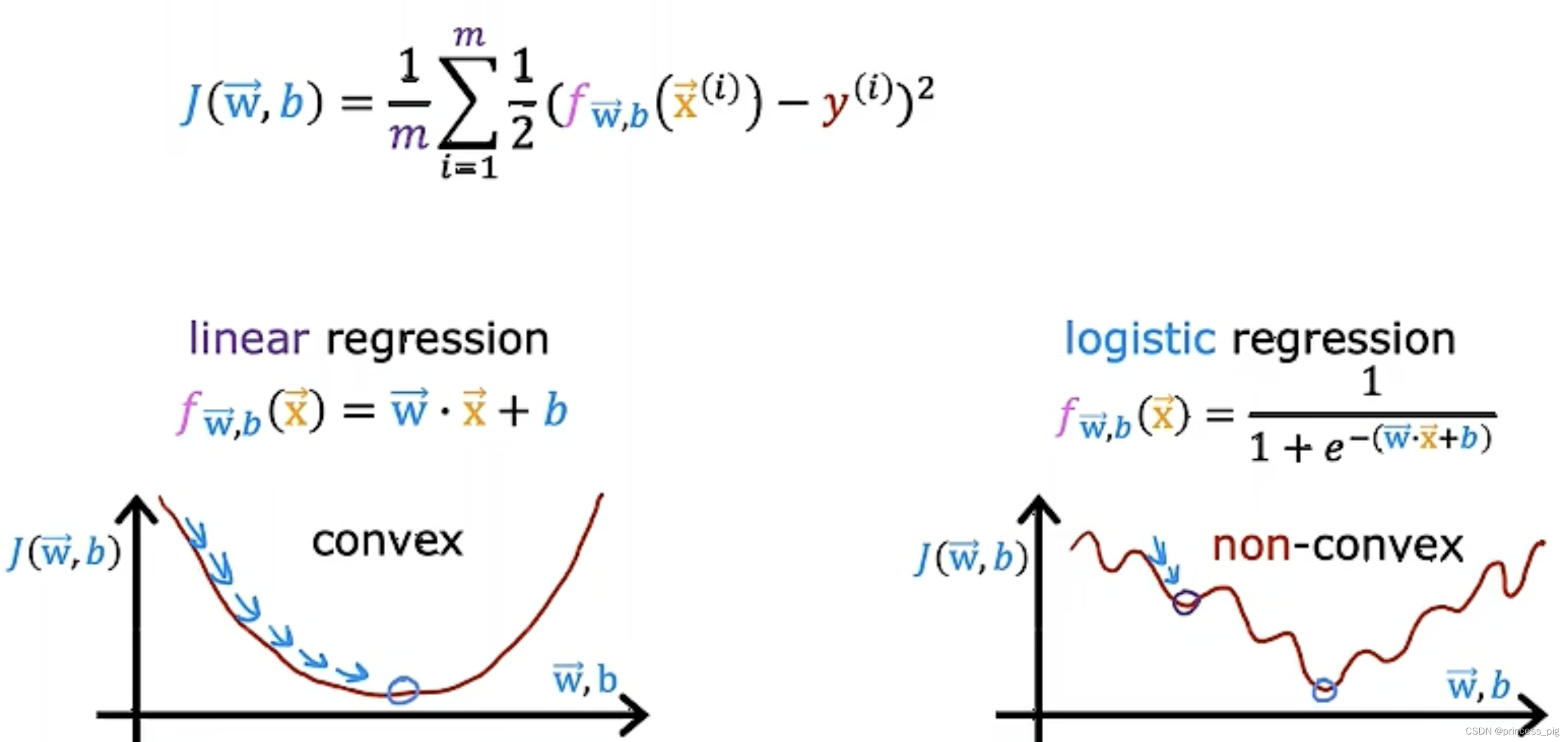
所以我们要用一个不一样的成本函数。
我们得到了一个新的成本函数:L() ,它的值和
相同,这个比较难推导,可以自己试一下(不建议)。
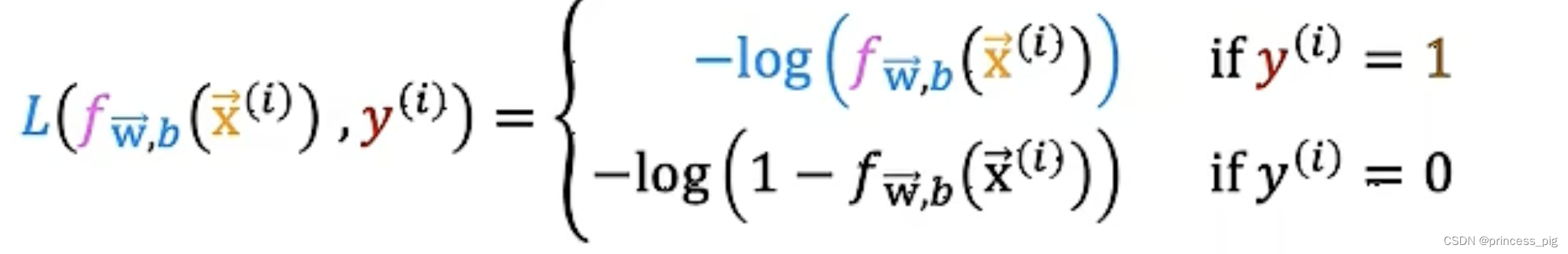
这时我们会得到两个对数函数,我们会在1和0时用到不同的函数去进行计算。
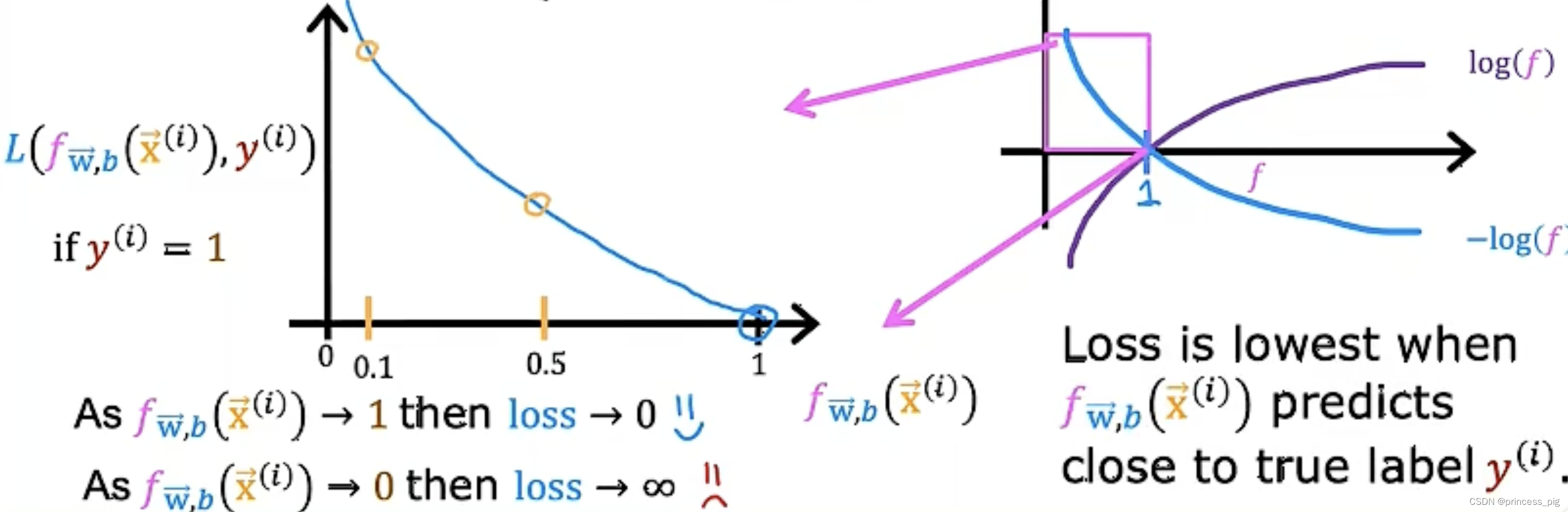
我们先看上面那一个方程,我们会发现预测的值越接近于1我们的损失就会越小,而我们接近于0的损失就会变大。同样的道理对于下面拿个方程。 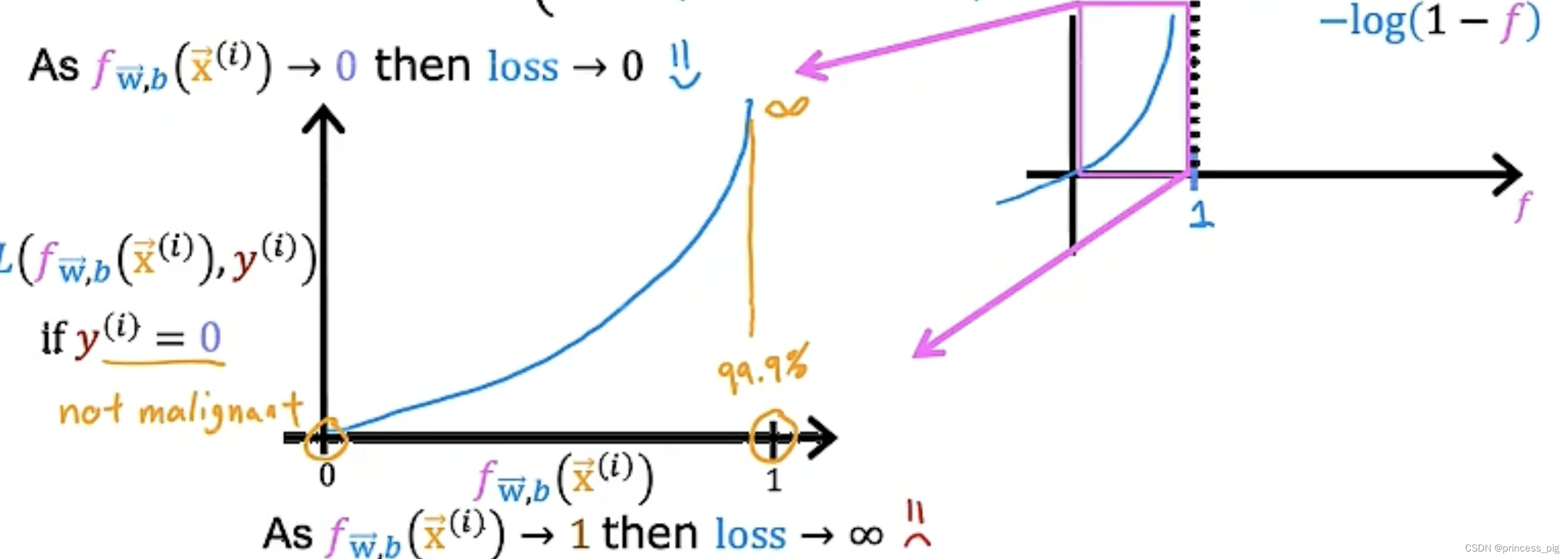
这里的损失函数,每一个都是一个单独的训练项,而不是一个集合。所以在这里的完整的成本函数写法是:
因为在这里我们的不是1就是0,所以我们可以简化我们的式子,那么它就变成了:
很明显它与我们在上面的式子是等价的。它是一种叫做最大似然估计的统计原理。
逻辑回归的梯度下降(gradient descent for logical regression):
在我们得到了我们的成本函数,接下来我们就要进行我们的梯度下降,还是一样的公式。
得到了我们的成本函数的式子:
然后我们还是用相同的方法进行我们的梯度下降。
和
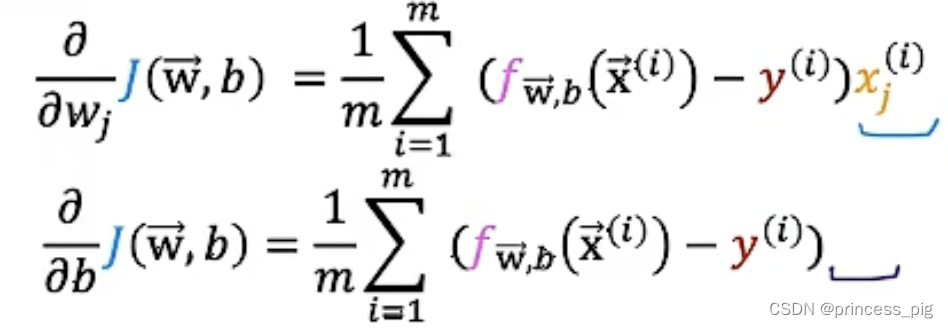
同样的道理,在这里的w,b的值是同时进行改变的,而没有先后的关系。两个偏导数算完之后我们才可以得到我们在上面的两个我们需要的特征值。
上面这个式子似乎和我们一开始在线性回归中用到的函数似乎是一样的但其实我们的f函数是完全不一样的,我们在我们的线性回归中,我们的函数是:,而在我们的逻辑回归中我们的函数是sigmoid函数(逻辑函数)。只是在我们算我们的梯度下降时我们用到的公式相同罢了。