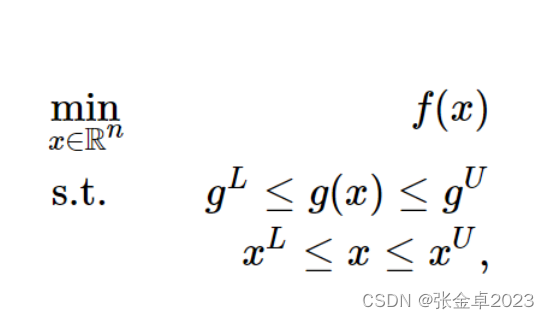目录
一、优化概念
1、一般优化问题
2、全局最优和局部最优
二、无约束优化
1、无约束优化概述
2、梯度方法
通用框架
线性搜索
回溯搜索
3、梯度下降
基本思想
实现流程
4、牛顿法
基本思想
实现流程
5、高斯牛顿法
6、LM法(Levenberg-Marquardt Method)
三、二次规划
1、凸函数与凸集合
2、凸优化问题
3、二次规划
四、非线性规划问题
一、优化概念
1、一般优化问题
对于一般优化问题可以如下表述:
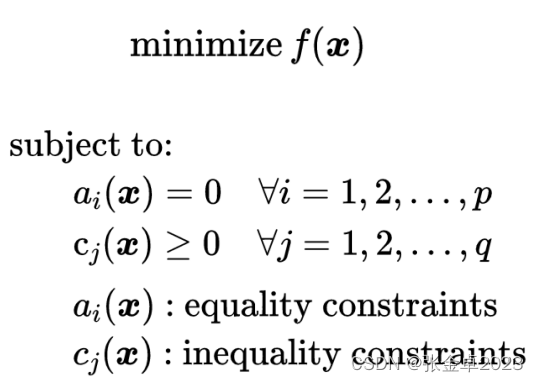
式中 f(x) 是目标函数,x是想要求解的决策变量,S是可行域,subject中的内容是关于变量的约束条件,由等式约束或不等式约束构成。
举一个简单的例子,如下图所示:
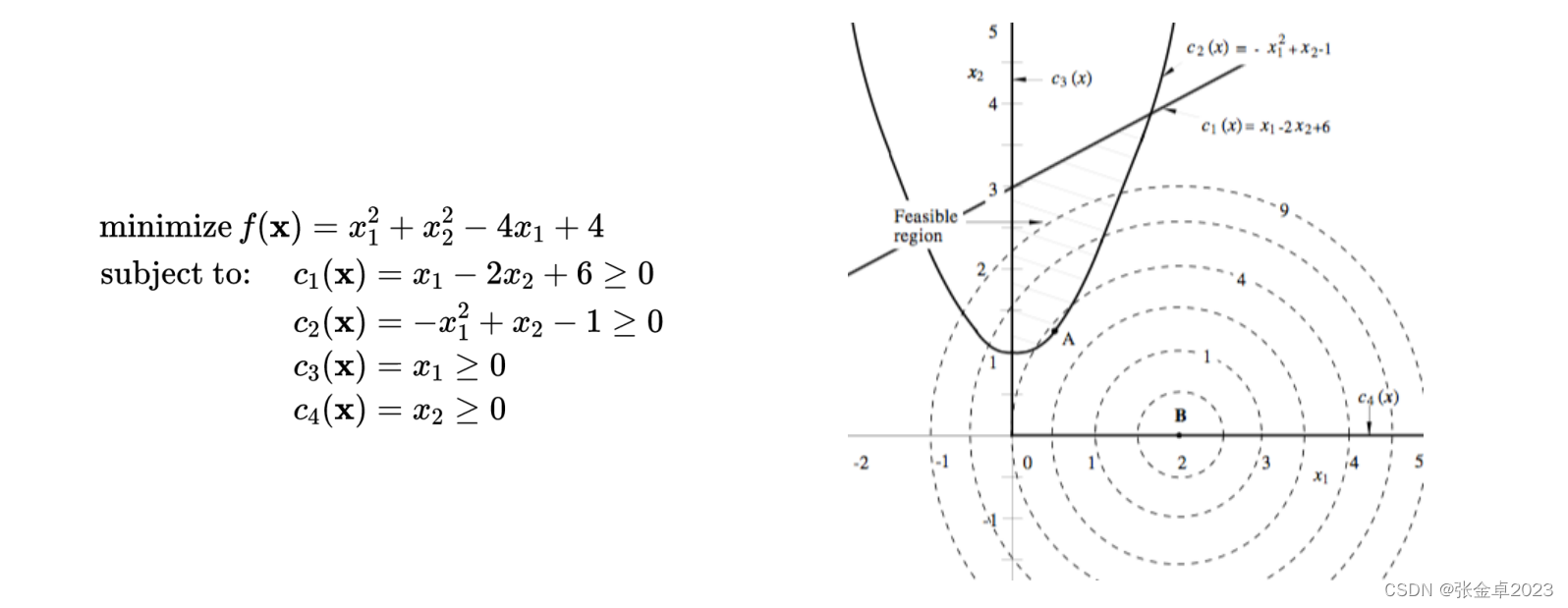
2、全局最优和局部最优
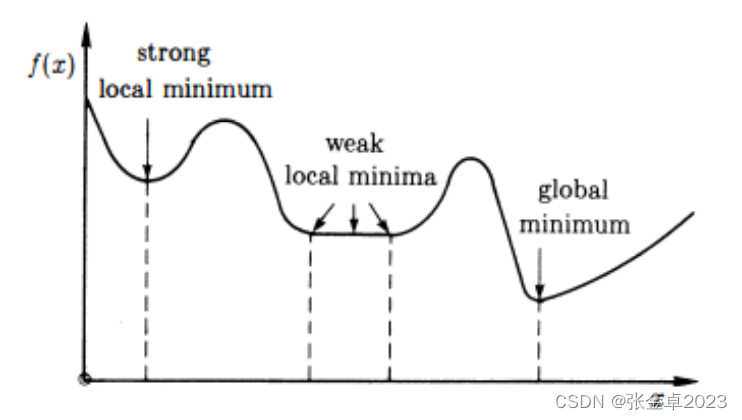
全局最优对应上图中的global minimum,是在整段函数上取得的最小值,而局部最优则对应的是在一个小的邻域中寻找最小值,与之相对应的有强局部最优和弱局部最优。强局部最优严格要求邻域内的其他点对应的函数值大于最小值,而弱局部最优要求邻域内的其他点对应的函数值大于等于最小值。
二、无约束优化
1、无约束优化概述
无约束优化是优化问题中一类较为容易解决的问题,在无约束优化中我们只需要找到最小化的目标函数和其依赖的变量,对于这些变量的值没有任何限制。最简单的数学表达式如下:

当函数f(x)是可微的,x是局部最优解的必要条件是当前x的梯度为0。
用来解决无约束优化问题的梯度法有如下几种:
- 梯度下降法
- 牛顿法
- 高斯牛顿法
- Levenberg-Marquardt Method
2、梯度方法
通用框架
对于一般的梯度方法可以用如下迭代公式:
式中x表示优化变量,表示第k次迭代优化变量的取值,
表示第k次迭代下降的方向,
表示关于下降方向的步长。
我们期望每经过一步,函数值下降,。
重复迭代过程直到满足某个收敛的条件,关于收敛条件有如下三种常见的定义:
在工程上我们往往会使用多种收敛条件的组合进行判断。
线性搜索
关于步长α可以通过线性搜索的方式取得,将该过程抽象为数学表达式如下:
式中 表示第k次迭代优化变量的取值,
表示第k次迭代下降的方向,对于线性搜索
是一个已知量,步长α就是我们要求解的未知量。
线性搜索可分为精确线性搜索和非精确线性搜索:
- 精确线性搜索:
,该函数表达的是要在给定下降方向上找到一个精确到α值使得函数值达到最小;
在工程实际中,对于一个复杂的目标函数我们很难直到一个准确的方向,想要通过一个近似得到的方向获得精确的步长显示是不合理的。
- 非精确线性搜索:不必严格寻找使得整体代价值最小的步长,只要代价值小于一定值就可以接受,如下图所示有两个满足条件的区间,相比较而言,非精确的线性搜索更加高效。

回溯搜索

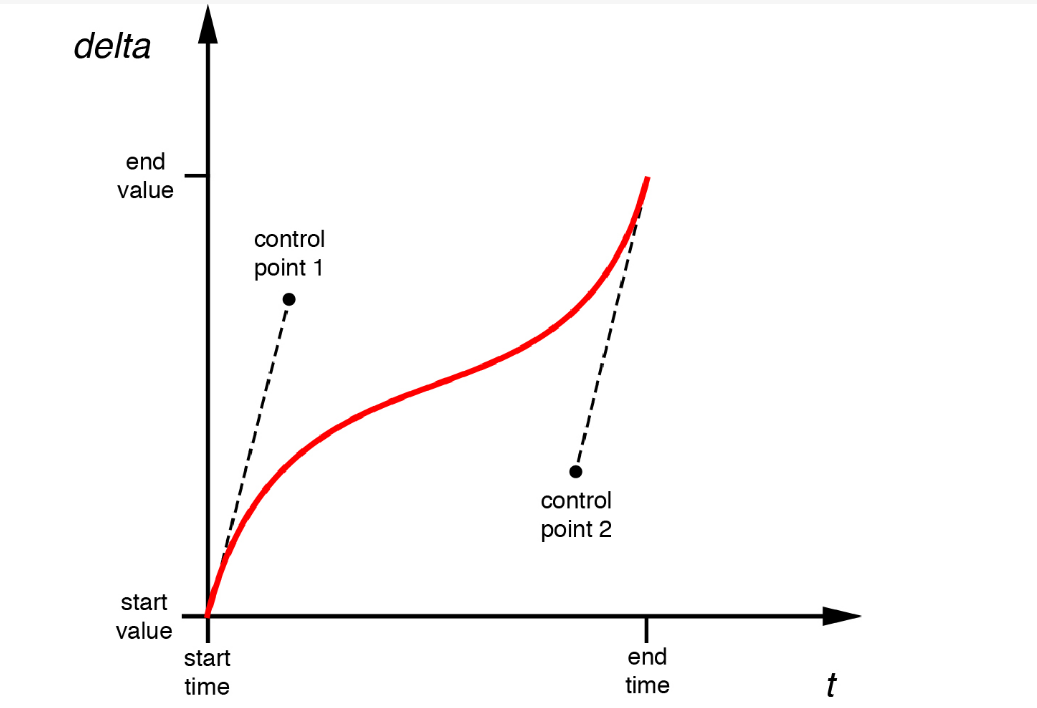
图中横轴t表示步长,下降方向△x对于某一点是已知的,在起点对其做泰勒展开可以得到一条切线,将切线乘对应的α因子可以得到放缓的线条。
对于回溯法,只要搜索得到的点在两条虚线之间就认为有效。具体的判断如下:
3、梯度下降
基本思想

在高等数学中我们学过梯度方向是一个函数值增长最快的方向,对应上图中的steepest ascent,而想要让代价函数的下降值最快则要沿着负梯度方向,梯度下降正是依赖于这种思想。
对于上图的二维函数,使用迭代框架,从起始点x0开始,每一步都朝着负梯度方向前进。
实现流程
 4、牛顿法
4、牛顿法
基本思想
相比于梯度下降这种一阶的方法(只用到了梯度的信息),牛顿法是一个二阶的方法。用一维函数来简述牛顿法的步骤:

第一步是在当前点进行二阶的泰勒展开;通过第二步是通过泰勒展开的方式对原函数进行近似,我们想利用二次函数的最优质找到合适的下降方向因此通过将第二步中得到的函数对进行求导即可到达第三步中的梯度函数;通过移项等方式得到最终第四步
的表达式。
实现流程

牛顿法的伪代码实现与梯度下降方式基本一致,只是牛顿法的前提是函数二阶可导,而梯度下降法只要一阶可导。
5、高斯牛顿法
高斯牛顿法是牛顿法的优化,它的最小化成本函数基于最小二乘的思想:
将累计求和的形式转换成向量的形式:
对F(x)向量进行一阶展开,得到:
再将展开得到的式子代入:
将平方项展开后对进行求导记得可到高斯牛顿的搜索方向:
将高斯牛顿得到的结果与牛顿法得到的结果进行对比,高斯牛电脑中J是表示F(x)函数的梯度,
等效于牛顿法中的
,而后面的
等效于牛顿法中的梯度。之所要有这样替代的操作,是因为当优化变量非常多时,在每一步迭代用牛顿法计算
是非常耗时的操作。
具体伪代码的实现流程如下:

6、LM法(Levenberg-Marquardt Method)
LM法是高斯牛顿法的优化,在高斯牛顿法中可能会出现是一个奇异矩阵或存在病态条件,此时下降方向的稳定性较差,导致算法出现发散。
LM法通过引入参数在梯度下降法和高斯牛顿法之间做动态地调整,公式如下:

三、二次规划
1、凸函数与凸集合
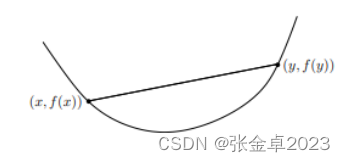
凸函数在数学上的精确定义如下:
在某个向量空间的凸子集中,有任意两个向量x,y有:
简单来说,就是f函数的值在连接f(x)和f(y)的线段下方;
对于凸集合,有如下定义:
对于一个集合C,若对于任意x,y∈C,有
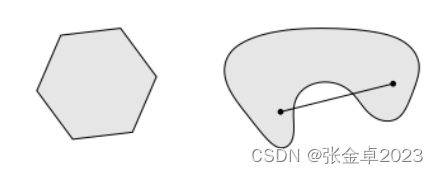
简单来说,对于凸集合内的任意两点,链接该对点的直线段上的每一个点也在这个集合内。如下图左侧就是一个凸集合,右侧就不是凸集合。
2、凸优化问题

对于上述优化处理,若满足都是凸函数,那么这种规划就是凸优化。
凸优化有以下几个优点:
- 可行集是凸集合;
- 凸函数的局部最优解必定是全局最优解
- 在理论和工程实际中,相比较其他优化方法,凸优化是比较好处理的。因此在自动驾驶规划领域,我们很多时候也会把问题建模成凸优化问题。
下面简单介绍几种在凸优化领域方法的定义:

- LP:linear program(线性规划)
- QP: quadratic program(二次规划)
- SOCP: second-order cone program(二阶锥规划)
- SDP: semidefinite program(半定规划)
- CP: cone program(锥规划)
本节我们主要关注二次规划问题。
3、二次规划

本节不重点二次规划原理和具体实现流程,主要将在工程实际中如何处理类似的二次规划问题。
QSOP求解器是一个数值优化包,用于求解形式为凸的二次规划。
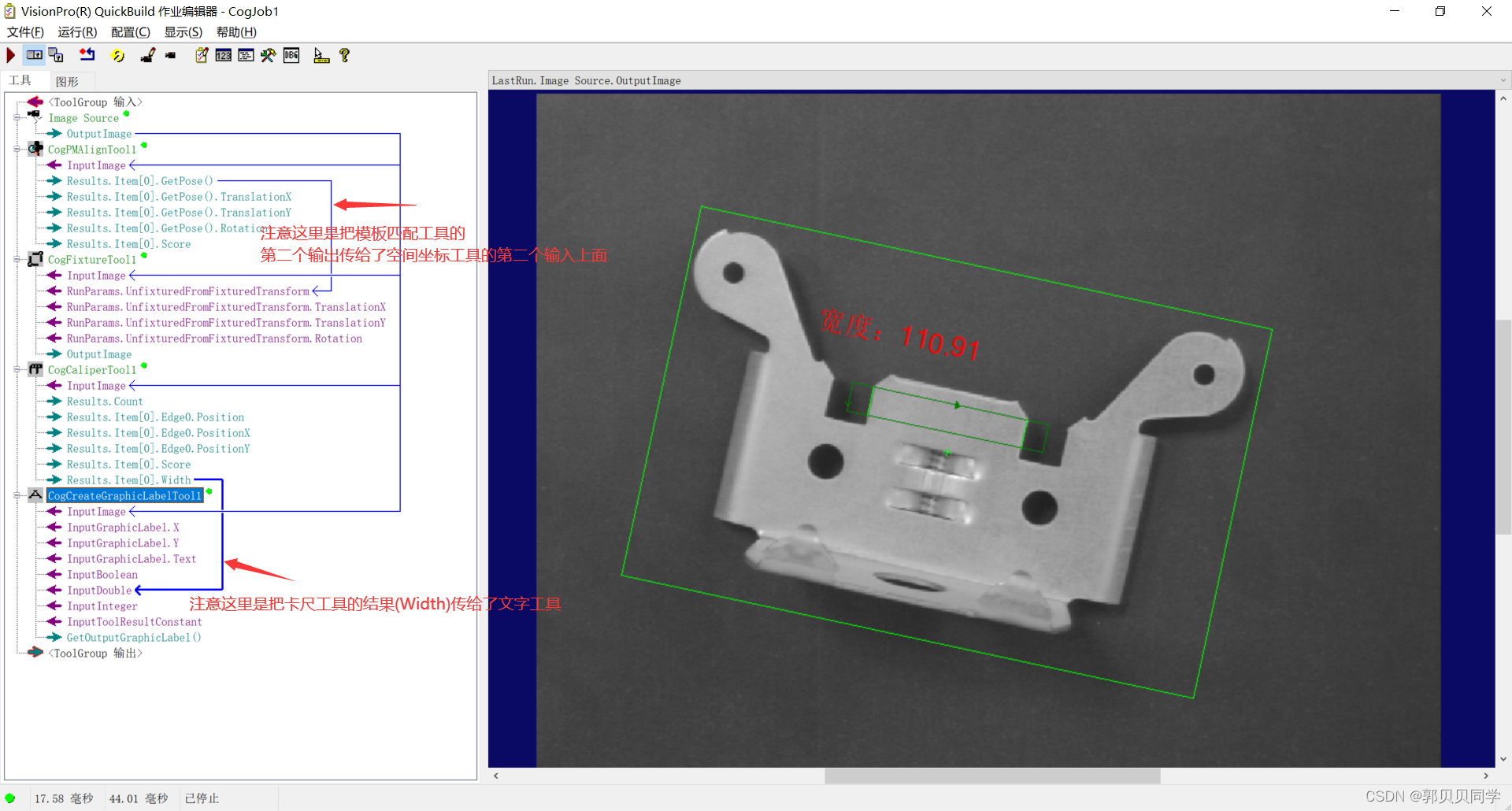
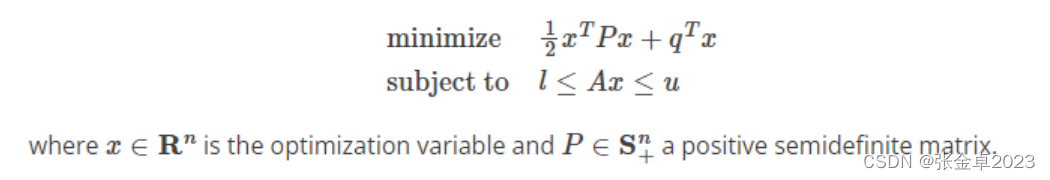 具体到代码层面来说:
具体到代码层面来说:

四、非线性规划问题
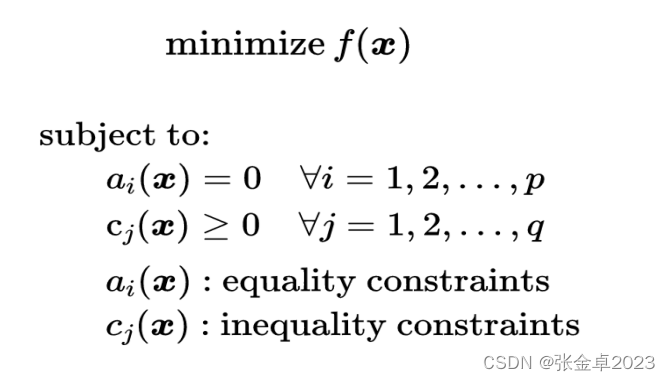
此处的非线性主要指的是目标函数和约束都是非凸的。
求解非线性规划问题有:
- 顺序二次规划(SQP)
- 内点法(IPM)
同样在工程上也有直接处理非线性规划问题的处理器——Ipop,该处理器基于内点法,主要思想是: