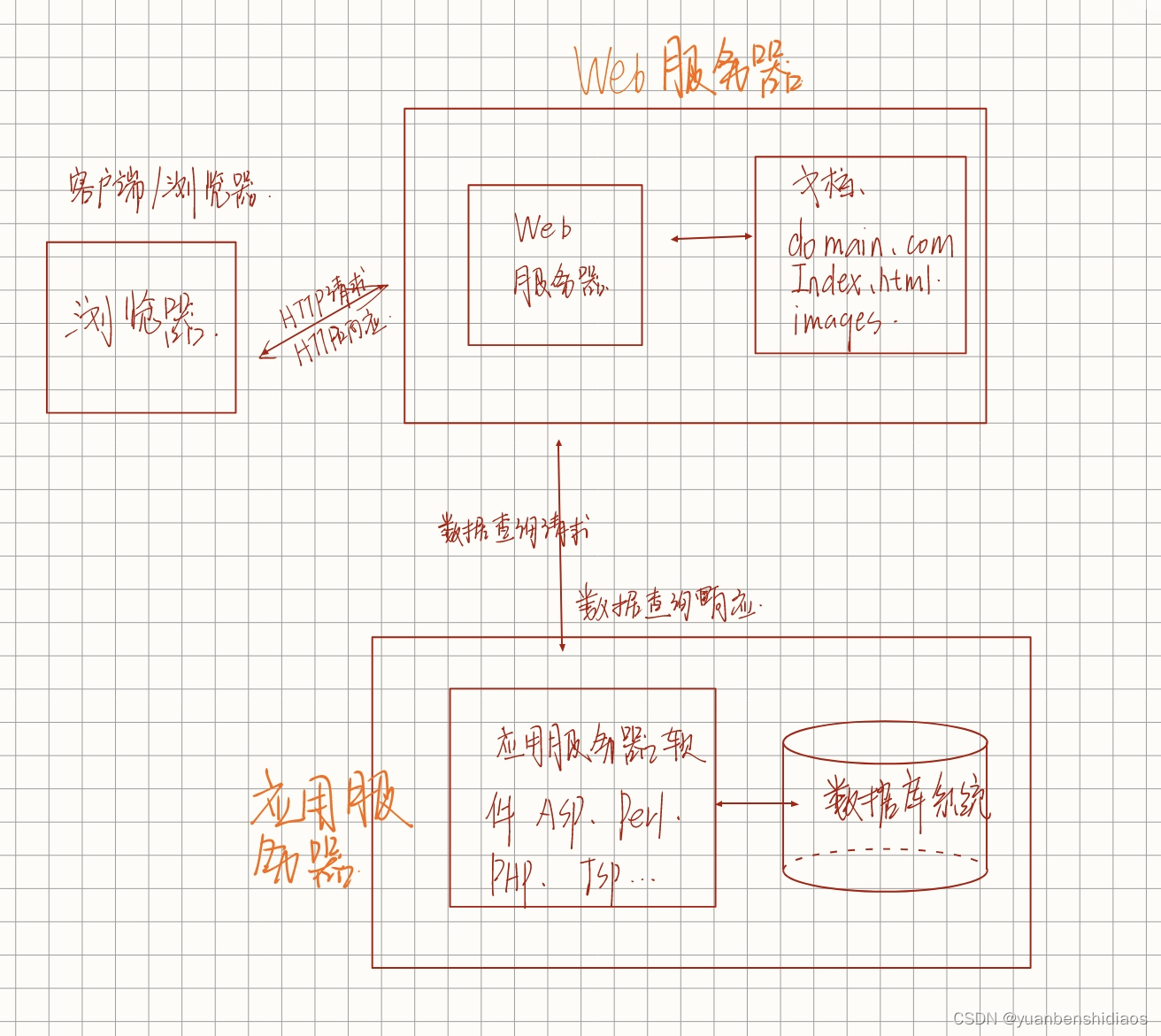
1.队列的链式操作

循环链表实现的链式队列中,头指针的变动主要取决于队列的操作。一般来说,在循环链表队列中,头指针front指向队列的头节点,尾指针rear指向队列的尾节点的下一个位置。
当进行入队(插入)操作时,头指针front通常不需要变动,只需要移动尾指针rear到新的节点位置,并将新节点连接到队列中。这样可以保持队列的循环性质,队列仍然可以正常工作。
当进行出队(删除)操作时,如果删除的是头节点(即队列中只有一个节点),则需要同时移动头指针front和尾指针rear到空队列状态。如果删除的不是头节点,只需移动头指针front到下一个节点位置即可。
总的来说,在循环链表实现的链式队列中,头指针front的变动通常与出队操作相关,而入队操作一般只需要移动尾指针rear。通过正确地维护头尾指针,可以有效地实现循环链表队列的操作。
2.线性结构和非线性结构以及存储结构
1.线性结构一般指的是栈和队列
2.非线性结构一般指的是树和图
3.存储结构分为顺序存储,链式存储,散列存储,索引存储
3.二叉树相关知识点
1.二叉树前i层节点数最多为 2^k-1
2.二叉树第i层节点数最多为 2^(k-1)
3.完全二叉树的前i层节点数是在2^i-1到2的i-1次方-1之间
4.度为m的树,前i层节点数最多为m^i-1
5.高度为h,度为m的树至少有 h+m-1个节点
6.边和节点个数的关系: 节点个数=边数+1
7.注意完全二叉树的节点个数和n0,n1,n2之间的关系**(n0=n2+1,n2=n0-1)**
8.二叉树的节点情况: i的左孩子为 2i,右孩子为 2i+1,当前层序为 log2^(i+1)
4.八大排序算法对应的时间复杂度和空间复杂度
- 冒泡排序:
时间复杂度: 平均情况为0(n^2),最快为0(n)
空间复杂度: 0(1) - 选择排序:
时间复杂度: 平均,最好,最坏情况都是0(n^2)
空间复杂度: 0(1) - 插入排序:
时间复杂度: 平均,最坏情况是 0(n^2),最好情况为 0(n)
空间复杂度: 0(1) - 归并排序:
时间复杂度: 平均,最好最坏的情况都是 0(nlogn)
空间复杂度: 0(n) - 快速排序:
时间复杂度: 平均为 0(nlogn),最好情况也是 0(nlogn),最坏情况为 0(n^2)
空间复杂度: 平均情况为 0(nlogn),最坏情况与归并排序类似,为 0(n) - 堆排序:
时间复杂度: 与快排和归并排序类似都是 0(nlogn),每一次分支的筛选运算时间为0(logn)
空间复杂度: 0(1)
在堆排序中,主要涉及两种操作:
建堆(Heapify):将一个无序序列构建成堆的过程,通常是从最后一个非叶子节点开始,依次向前对每个非叶子节点进行筛选操作,确保满足堆的性质。
调整堆(Heapify Down):在堆排序过程中,将堆顶元素取出后,需要对剩余元素进行调整,使其重新满足堆的性质。
对于堆排序中的筛选操作,时间复杂度取决于树的高度,而二叉堆的高度为 O(log n),因此对一个分支节点进行筛选的时间复杂度为 O(log n)。因为在每次筛选中,都是沿着树的高度进行比较和交换操作,所以时间复杂度与树的高度成正比。
总体来说,堆排序的时间复杂度为 O(n log n),其中建堆的时间复杂度为 O(n),每一次调整堆的时间复杂度为 O(log n),共进行 n-1 次调整。
- 希尔排序:
时间复杂度: 平均情况与堆排序,快速排序,归并排序类似,都是 0(nlogn),最坏情况为 0(n^2)
空间复杂度: 0(1)
总结:
1.空间复杂度为1的有希尔排序和堆排序(nlogn的时间复杂度),然后插入排序和选择排序,冒泡排序也是1(但是时间复杂度为n^2)
2.空间复杂度为nlogn的仅有快速排序,它的时间复杂度和空间复杂度都是0(nlogn)
5.散列存储的两种方法
1.链式散列(Chaining):
链式散列使用数组与链表相结合的方式来解决哈希冲突。具体来说,散列表的每个槽位(桶)都存储一个链表或者其他形式的动态数据结构,当发生哈希冲突时,新元素被插入到对应槽位的链表中。这样,不同关键字映射到同一个槽位的情况下,可以通过链表解决冲突,并保证元素的唯一性。
优点:实现简单,适用于动态数据集合。
缺点:链表长度过长时会影响查找效率,需要一定的额外空间存储指针。
2.线性探测法(Linear Probing):
线性探测法是一种解决哈希冲突的方法,当发生哈希冲突时,线性探测法会依次检查散列表中的下一个位置是否为空,直到找到空位置为止。如果该位置已被占用,则继续向后查找,直到找到空位置或者遍历整个散列表。
优点:相对简单,适用于小规模数据集合。
缺点:容易产生堆积,即当冲突较多时,会出现线性探测长度过长的情况,影响查询性能。
总的来说,链式散列适用于动态数据集合,而线性探测法适用于小规模数据集合。在实际应用中,根据具体场景和需求选择合适的散列存储方法。
6.图的知识点
1.首先是完全图和连通图的区分:
**完全图:**任意两个节点都有边的则为完全图(比如四个节点有6条边);
**连通图:**任意两个节点都有一条连通的路;
区别: 完全图n个顶点有n(n-1)/2条边,而连通图至少有n-1条边(比如两个节点)
(注意连通非连通情况,+1节点)
无向图: 度是边的两倍(没有入度和出度的概念)
2.强连通图和连通分量,极大连通分量,生成树的区别:
强连通图:有方向,双向路径,最少边数为n(环),至多为n(n-1)
(强连通图不能保证任何顶点到其他所有顶点都有弧)
连通分量: 相当于极大连通子图(子图极大,连通)
极小连通分量 边少的连通子图(生成树,所以无环)
3.无向完全图和有向完全图区别:
每个节点之间都有边,为1/2(n(n-1));
两个顶点之间都存在方向相反的两条弧:n(n-1);
4.强连通图和有向完全图区分:
结论: 有向完全图一定为强连通图 (有边有方向),但是强连通图不一定是有向完全图
因为: 强连通图不能保证任何顶点到其他所有顶点都有弧,可能只与其中之一之间有弧
5.顶点和边的关系:
n个顶点最多n-1条边(度),算入读出度,n个顶点最大度可达到2n-2
6.边的数量和生成树数量关系:
n个顶点,成为一个环,有n个边,n个边有n颗生成树
7.无向图中顶点和边的关系:
在一个连通的无向图中,当顶点数等于边数加一时,这个图就是一棵树。这个关系可以用来描述树的特性之一。
一棵树是一种特殊的无环连通图,具有以下特点:
1.所有的顶点之间都是连通的,且存在环(即无回路)。
2.恰好有n-1条边,其中n为顶点数;也就是说n-1条边可以保证n个顶点连通
因此,在一棵树中,顶点数等于边数加一,即 n = e + 1,其中n为顶点数,e为边数。
8.连通分量和树的关系:
树的个数=连通分量个数=节点n-边数e
9.邻接表:
有向图和无向图中,在邻接表中的边节点就为自己身上的边数,有向图为e,无向图为2*e
7.算法的质量
四个角度: 正确性,易读性,强壮性,高效率
8.树的广义表
广义表可以方便地表示各种树形结构,包括二叉树、多叉树等。例如,一个广义表可以表示如下的树形结构:
(A, (B, C), (D, (E, F, G)))
树形结构如下(括号同一级别,是兄弟节点,外为父节点):
A
/ \
B C
/
D
/ \ \
E F G

9.前缀,中缀,后缀表达式
1.前缀表达式:
1.前缀表达式又称波兰式,前缀表达式的运算符位于操作数之前。
举例: (3+4)*5-6的前缀表达式为 - * + 3 4 5 6
方法: 从右至左扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对他们做相应的计算
如何写: 括号里的运算符最靠右,数字正常顺序,其余运算符按先后顺序来
2.中缀表达式:
日常
3.后缀表达式:
1.与前缀表达式相似,只是运算符位于操作数之后。
a+(b-c)*d——>前缀:+ a * - b c d;后缀:a b c - d * +

10.叉树中,为什么有n个节点,其中有n-1个指针域放了地址,n+1个指针式空指针
现在来解释一下为什么有 (n-1) 个指针域存放了地址,而有 (n+1) 个指针域是空指针。
首先,我们知道一个二叉树有以下性质:
1.如果一个二叉树是空树,即没有节点,那么它自然不包含任何指针。
2.如果一个二叉树只有一个节点,那么该节点是根节点,它的左右子树为空,因此有两个空指针。
3.对于包含 (n) 个节点的非空二叉树,由于每个节点都有一个指向左子树和一个指向右子树的指针域,所以总共有 (2n) 个指针域。其中,有 (n-1) 个指针域存放了地址,用来连接各个节点(类似于无向连通图,n点有n-1边),而有 (n+1) 个指针域是空指针。
11.根据数组绘画线性表:

根据下标找next即可