思路dfs:
首先通过两层for循环遍历每一个点,如果这个点为0或者2(这个2是什么呢?是在遍历该点以及该点连成的这一片区域中,因为通过深度优先搜索,遍历该点就等于遍历这一片区域,遍历这篇区域中的点的同时,将这些元素标记为2,即代表这篇区域已经遍历过),那么遍历下一个点。遇到一个新的区域则cnt++。
那么怎么进行深度搜索呢?即如果该点=1,那么将该点的上方、下方、左方、右方送入dfs。
dfs代码:
C++:
class Solution {
public:
int p_m[4]={-1,1,0,0};
int p_n[4]={0,0,-1,1};
void dfs(vector<vector<char>>& grid,int i,int j,int m,int n){
for(int k=0;k<4;k++){
int x=i+p_m[k];
int y=j+p_n[k];
if(x>=0 && x<m && y>=0 && y<n){
if(grid[x][y]=='0'||grid[x][y]=='2'){
continue;
}
else{
grid[x][y]='2';
dfs(grid,x,y,m,n);
}
}
}
}
int numIslands(vector<vector<char>>& grid) {
int m=grid.size();
int n=grid[0].size();
//cout<<m<<' '<<n<<endl;
int cnt=0;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(grid[i][j]=='2'||grid[i][j]=='0'){continue;}
else{
dfs(grid,i,j,m,n);
cnt++;
}
}
}
return cnt;
}
};注意:二维数组中,求行数为
int m=grid.size();求列数为
int n=grid[0].size();python:
class Solution:
def dfs(self,grid:List[list[str]],i:int,j:int,m:int,n:int) -> int:
p_m=[-1,1,0,0]
p_n=[0,0,-1,1]
for k in range(4):
x=i+p_m[k]
y=j+p_n[k]
if x>=0 and x<m and y>=0 and y<n:
if grid[x][y]=='0' or grid[x][y]=='2':
continue
else:
grid[x][y]='2'
self.dfs(grid,x,y,m,n)
def numIslands(self, grid: List[List[str]]) -> int:
m=len(grid)
n=len(grid[0])
cnt=0
for i in range(m):
for j in range(n):
if grid[i][j]=='2' or grid[i][j]=='0':
continue;
else:
self.dfs(grid,i,j,m,n)
cnt+=1
return cntbfs思路:
与dfs类似,遍历每个元素时,如果该元素的值为1,那么将其入队列,并且考虑其上下左右的元素,如果周围元素值为1,将其也入队列。遍历一个元素时,如果该值为1,那么代表访问了一个新的区域,则cnt++。
代码:
C++:
class Solution {
public:
deque<pair<int,int>> q;
int p_x[4]={-1,1,0,0};
int p_y[4]={0,0,1,-1};
int numIslands(vector<vector<char>>& grid) {
int cnt=0;
int m=grid.size();
int n=grid[0].size();
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(grid[i][j]=='0'||grid[i][j]=='2'){continue;}
else{cnt++;}
q.push_back({i,j});
while(!q.empty()){
pair<int,int> temp=q.front();
q.pop_front();
int temp_x=temp.first;
int temp_y=temp.second;
if(grid[temp_x][temp_y]=='0'||grid[temp_x][temp_y]=='2'){continue;}
else{
grid[temp_x][temp_y]='2';
for(int k=0;k<4;k++){
int x=temp_x+p_x[k];
int y=temp_y+p_y[k];
if(x>=0 && x<m && y>=0 && y<n){
if(grid[x][y]=='0'||grid[x][y]=='2'){continue;}
else{
q.push_back({x,y});
}
}
}
}
}
}
}
return cnt;
}
};明显可以看到bfs要比dfs慢的多。

 python:
python:
明天继续更啦~
前序中序遍历二叉树
并查集做该道题
bfs的python写法


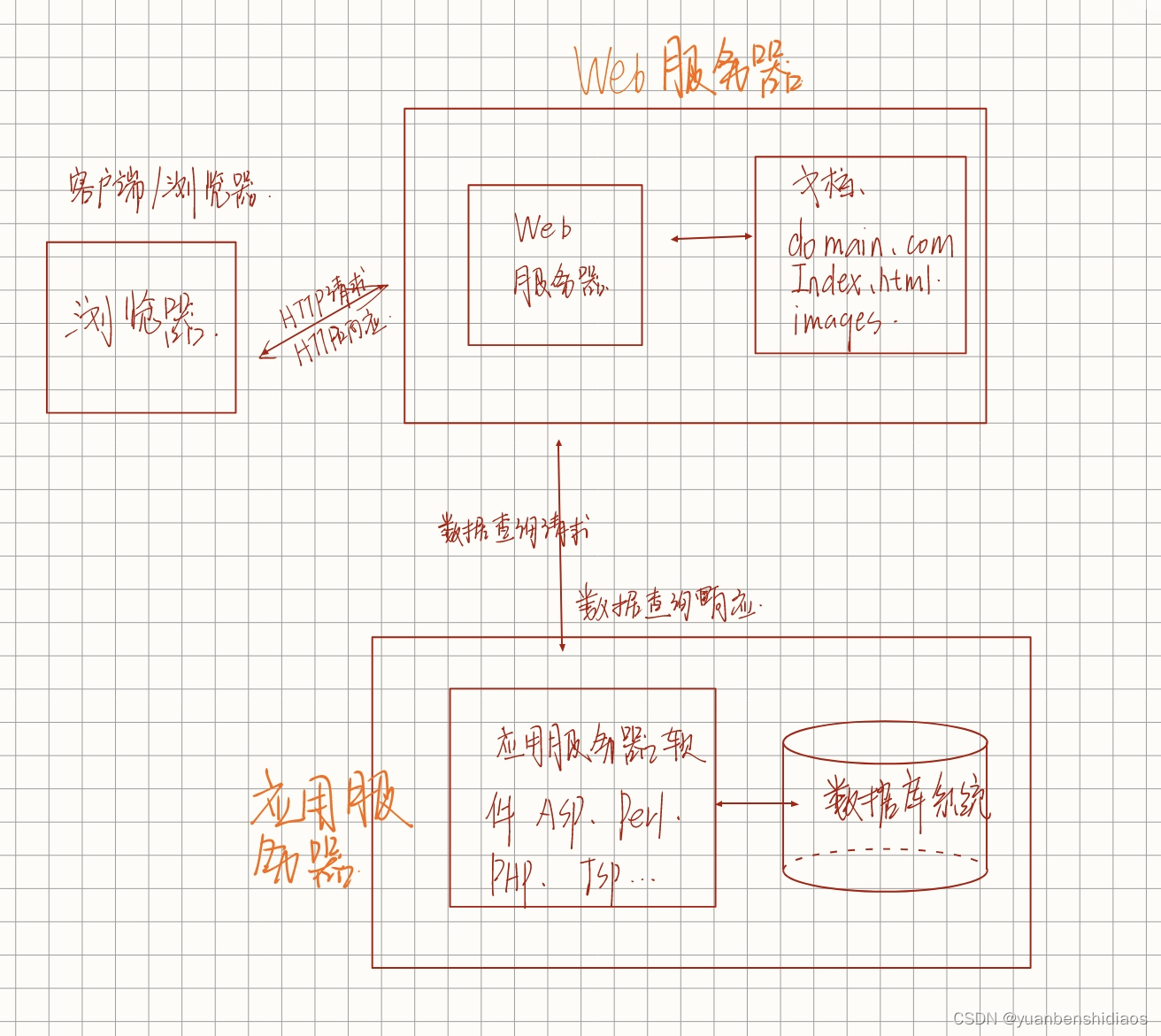



![XSS漏洞--概念、类型、实战--分析与详解[结合靶场pikachu]](https://img-blog.csdnimg.cn/direct/27d9ed9fb00641fab2e1722f4414a685.png)