题目:
给定两个字符串 A 和 B,现在要将 A 经过若干操作变为 B,可进行的操作有:
- 删除–将字符串 A 中的某个字符删除。
- 插入–在字符串 A 的某个位置插入某个字符。
- 替换–将字符串 A 中的某个字符替换为另一个字符。
现在请你求出,将 A 变为 B 至少需要进行多少次操作。
输入格式
第一行包含整数 n,表示字符串 A 的长度。
第二行包含一个长度为 n 的字符串 A。
第三行包含整数 m,表示字符串 B 的长度。
第四行包含一个长度为 m 的字符串 B。
字符串中均只包含大小写字母。
输出格式
输出一个整数,表示最少操作次数。
数据范围
1≤n,m≤1000
输入样例:
10 AGTCTGACGC 11 AGTAAGTAGGC输出样例:
4
DP:

状态表示 f[i][j]
- 集合 : 所有吧a中的前i个字母 变成 b中前j个字母的集合的操作集合
- 属性 : 所有操作中操作次数最少的方案的操作数
状态计算
状态划分 以对a中的第i个字母操作不同划分
- 在该字母之后添加
添加一个字母之后变得相同,说明没有添加前a的前i个已经和b的前j-1个已经相同
即 : dp[i][j] = dp[i][j-1] + 1
- 删除该字母
删除该字母之后变得相同,说明没有删除前a中前i-1已经和b的前j个已经相同
即 : dp[i][j] = dp[i-1][j] + 1
- 替换该字母
替换说明对应结尾字母不同,则看倒数第二个
即: dp[i][j] = dp[i-1][j-1] + 1
- 啥也不做
对应结尾字母相同,直接比较倒数第二个
即: dp[i][j] = dp[i-1][j-1]
代码:
import java.io.*;
import java.util.*;
class Main{
static int N = 1010;
static int n,m;
static char[] a = new char[N];
static char[] b = new char[N];
static int[][] f = new int[N][N];
public static void main(String[] args) throws IOException{
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(in.readLine());
String s = in.readLine();
for(int i=1;i<=n;i++)
a[i] = s.charAt(i-1);
m = Integer.parseInt(in.readLine());
s = in.readLine();
for(int i=1;i<=m;i++)
b[i] = s.charAt(i-1);
// 初始化
for(int i=0;i<=n;i++)
f[i][0] = i; // 只能执行删除操作
for(int i=0;i<=m;i++)
f[0][i] = i; // 只能执行添加操作
// DP
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(a[i]==b[j]) f[i][j] = f[i-1][j-1];
else{
f[i][j] = Math.min(f[i-1][j]+1,f[i][j-1]+1);
f[i][j] = Math.min(f[i][j],f[i-1][j-1]+1);
}
}
}
System.out.println(f[n][m]);
}
}DP
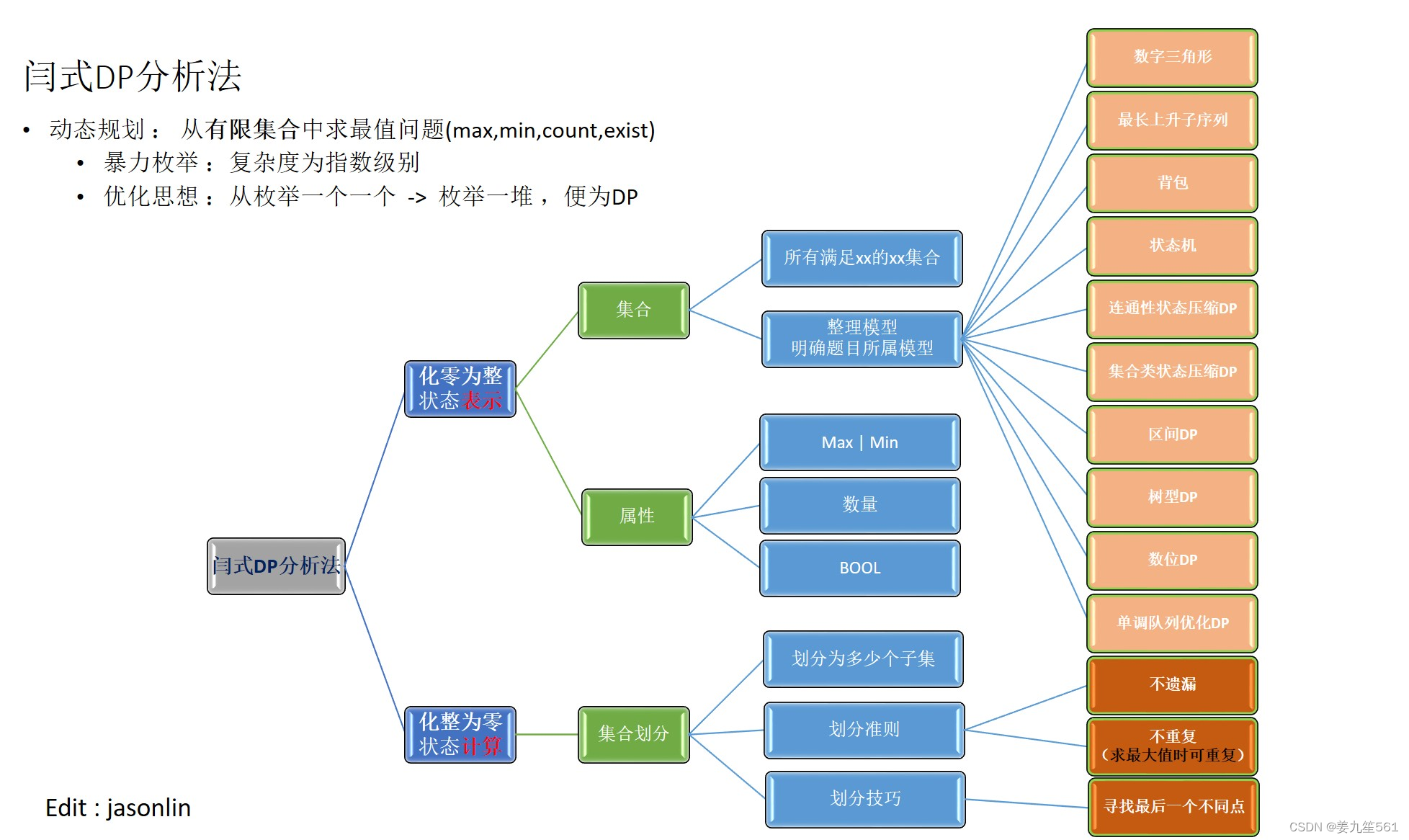
该图片来自 AcWing 902. 最短编辑距离【闫式DP大法好:)】 - AcWing