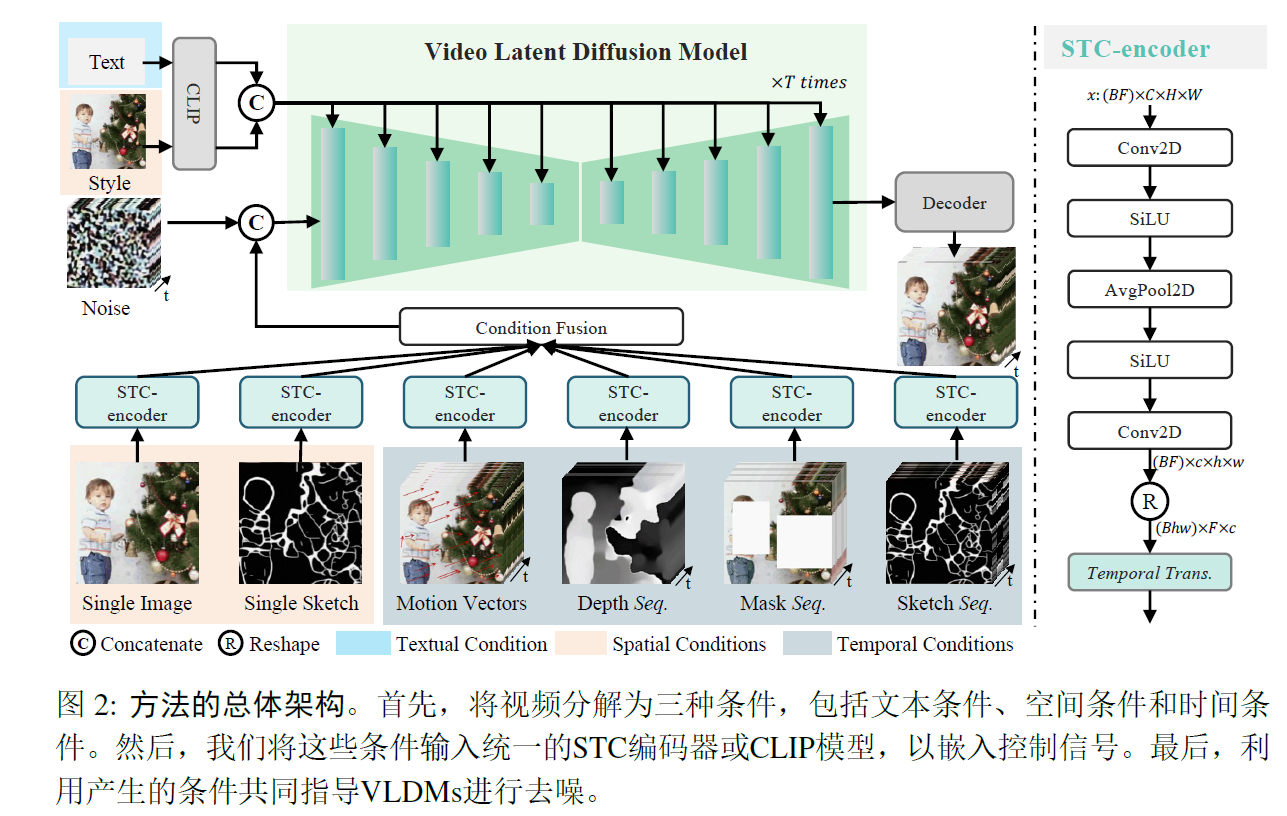
题意
大小为 k 的滑动窗口从整数数组 nums 的最左侧移到最右侧，只能看到滑动窗口中的 k 个数字，窗口每次向右移动一位。

返回滑动窗口的最大值。

示例 1：
输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：

示例 2：
输入：nums = [1], k = 1
输出：[1]

提示：

1 <= nums.length <= 105
-104 <= nums[i] <= 104
1 <= k <= nums.length

普通队列是限制仅在队尾进行插入，在队头进行删除操作的线性表，队列的插入叫做入队列，队列的删除叫做出队列。
双端队列则是放开了这个限制，在队头和队尾两端都可以进行入队和出队操作的队列。
单调队列，所有队列里的元素都是按递增（递减）的顺序队列，这个队列的头是最小（最大）的元素。

题解
首先窗口向右滑动的过程就是将窗口最左侧的元素删除，同时在窗口的最右侧添加一个新的元素，这就要用到双端队列，然后找双端队列中的最大元素。

那剩下就是如何找到滑动窗口中的最大值。

那我们就可以只在队列中保留可能成为窗口最大元素的元素，去掉不可能成为窗口中最大元素的元素。

想象一下，如果要进来的是个值大的元素，那一定会比之前早进去的值小的元素晚离开队列，而且值大的元素在，都没值小的元素啥事，所以值小的元素直接弹出队列即可。

这样队列里其实维护的一个单调递减的单调队列。

python：

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:

        # 如果数组为空或 k = 0，直接返回空
        if not nums or not k:
            return []
        # 如果数组只有1个元素，直接返回该元素
        if len(nums) == 1:
            return [nums[0]]

        # 初始化队列和结果，队列存储数组的下标
        queue = []
        res = []

        for i in range(len(nums)):
            # 如果当前队列最左侧存储的下标等于 i-k 的值，代表目前队列已满。
            # 但是新元素需要进来，所以列表最左侧的下标出队列
            if queue and queue[0] == i - k:
                queue.pop(0)

            # 对于新进入的元素，如果队列前面的数比它小，那么前面的都出队列
            while queue and nums[queue[-1]] < nums[i]:
                queue.pop()
            # 新元素入队列
            queue.append(i)

            # 当前的大值加入到结果数组中
            if i >= k-1:
                res.append(nums[queue[0]])

        return res