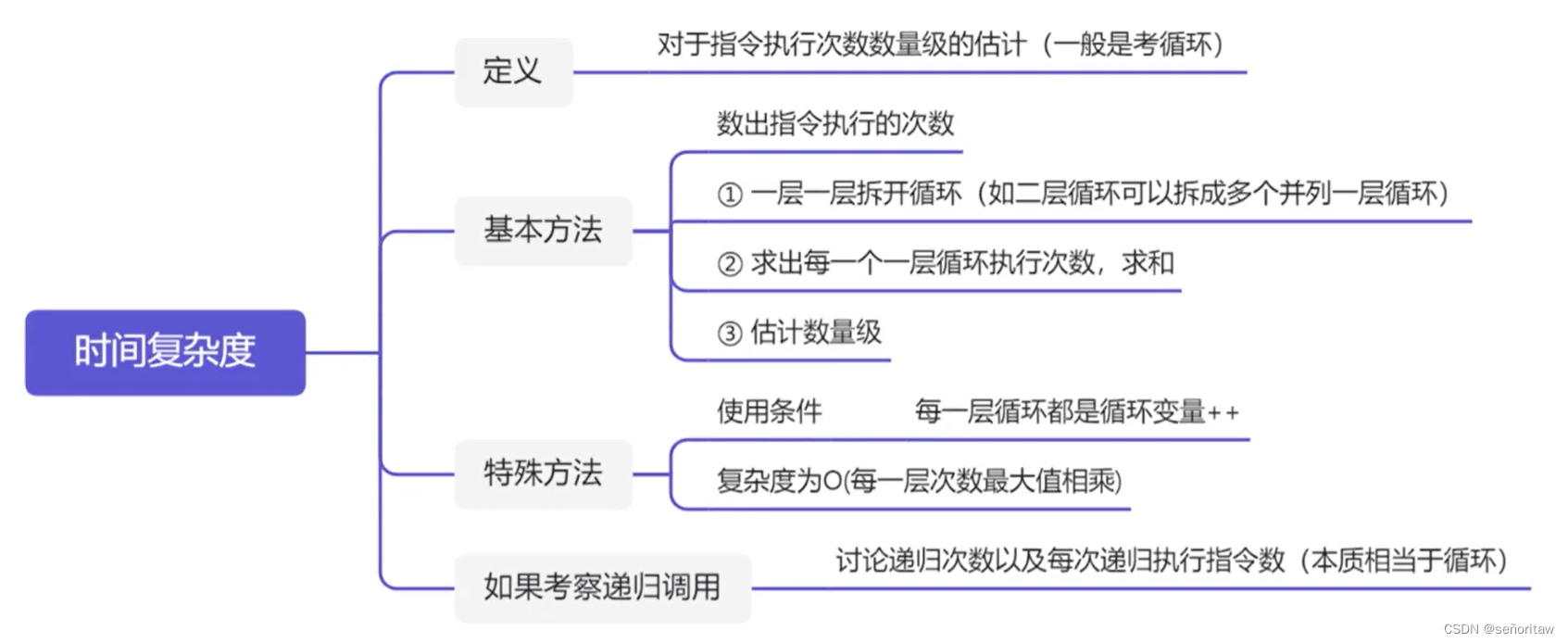
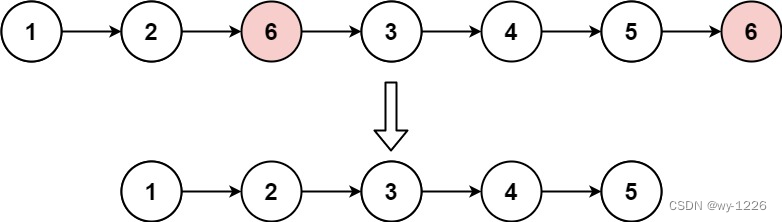
本题是一个经典的单调队列题。不过用优先队列也能解决。

一、优先队列

        在使用优先队列时，我们会遇到这样的问题：如何将一个目标数从优先队列中弹出？如果使用stl这是办不到的，虽然可以自行实现这样的功能。但是我们可以这样思考，我们保存数的位置信息延迟出队，当一个数在堆顶时，判断其是否在窗口中，不在窗口中则舍弃，一直找到在窗口中的数。判断是否在窗口中只需要保存这个数入队时的位置信息，在窗口之外则舍弃。 由于每个数进入优先对列（排序） 和 出优先对列 最多一次，则时间复杂度为nlogn+n。

时间复杂度：O（nlogn）<每个数进队进行一次logn排序，每个数进队出队最多一次>

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        priority_queue<pair<int,int> > Q;
        vector<int> ans;
        for(int i=0;i<k;++i) Q.push({nums[i],i});//这里first成员一定要是数值
        int len=nums.size()-k;
        for(int i=0;i<len;++i){
            while(Q.top().second<i) Q.pop();
            ans.push_back(Q.top().first);
            Q.push({nums[i+k],i+k});
        }
        while(Q.top().second<len) Q.pop();
        ans.push_back(Q.top().first);
        return ans;
    }
};

二、单调队列

        单调队列实际上就是时刻保存一个按顺序站好队的队列，这个队列的特殊性是不保存无效成员，且队头一定是当前答案。一旦更能成为答案的出现了，就不再保存不能成为答案的成员。

        相当于n个人排成一对，小明想依次记录每k个人的身高中最高的那一个。如果小明发现某次的k个人中有以个人比前面的人都高，那么小明在接下来看最高的人时，根本不用再记着这个人前面的人，因为他们在后面不会起到作用。虽然这个人后面的人可能比较矮，但可能在之后是最高的呀，因此还需要记录着。对于每一个人都是如此，他前面的比它矮的都没有用了，因此可以维护一个双端队列，在考虑某个人时，这个人如果比队列后面的人高，则把这些人出队，接下来就不再考虑了，但是队头的人一定是最高的吗？ 是的，但是还需要看看它是否在被考虑的k个人中。

        每个数入队出队最多一次，不需要进行排序，时间复杂度O(n)

记录身高以及位置信息：

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        deque<pair<int,int>> myque;
        int len=nums.size()-k;
        vector<int> ans;
        for(int i=0;i<k;++i) {
            while(!myque.empty()&&myque.back().first<=nums[i]) myque.pop_back();
            myque.push_back({nums[i],i});
        }
        for(int i=0;i<len;++i) {
            while(!myque.empty()&&myque.front().second<i) myque.pop_front();
            ans.push_back(myque.front().first);
            int temp=i+k;
            while(!myque.empty()&&myque.back().first<=nums[temp]) myque.pop_back();
            myque.push_back({nums[temp],temp});
        }
        while(myque.front().second<len) myque.pop_front();
        ans.push_back(myque.front().first);
        return ans;
    }
};

实际上不用记录身高，因为身高可以用位置信息直接得到（但优先队列不一样，是因为优先队列要在内部排序）：

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        deque<int> myque;
        int len=nums.size()-k;
        vector<int> ans;
        for(int i=0;i<k;++i) {
            while(!myque.empty()&&nums[myque.back()]<=nums[i]) myque.pop_back();
            myque.push_back(i);
        }
        for(int i=0;i<len;++i) {
            while(!myque.empty()&&myque.front()<i) myque.pop_front();
            ans.push_back(nums[myque.front()]);
            int temp=i+k;
            while(!myque.empty()&&nums[myque.back()]<=nums[temp]) myque.pop_back();
            myque.push_back(temp);
        }
        while(myque.front()<len) myque.pop_front();
        ans.push_back(nums[myque.front()]);
        return ans;
    }
};