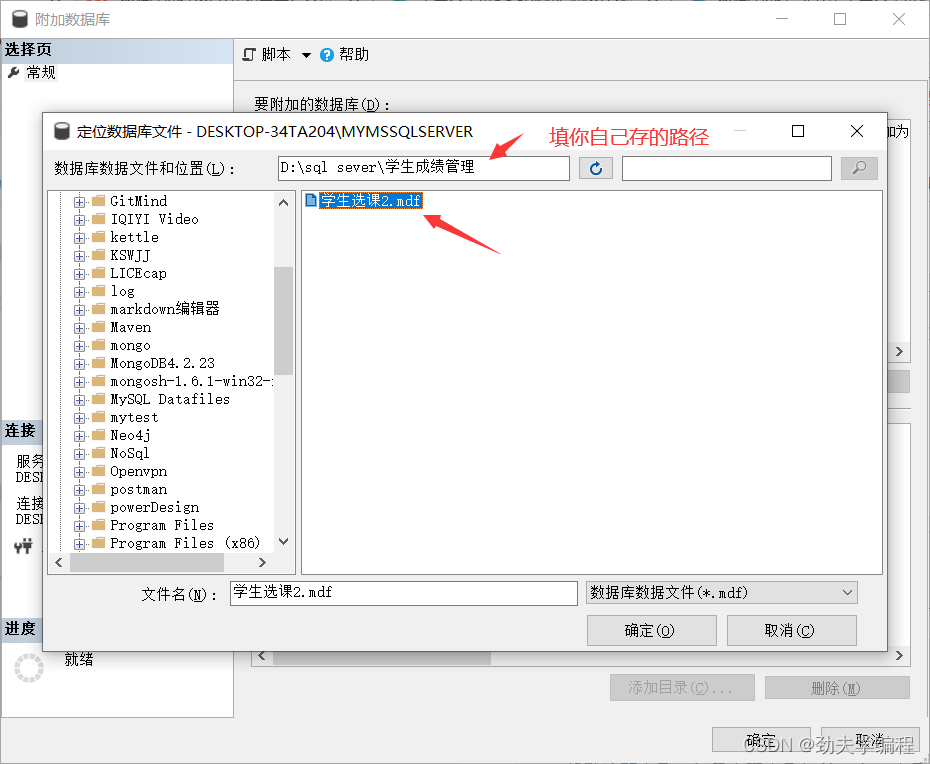
目录

一.特点

二.算法思想

三.公式证明

四.next数组及其练习

 五.找规律计算next[k]

六.代码实现

---

一.特点

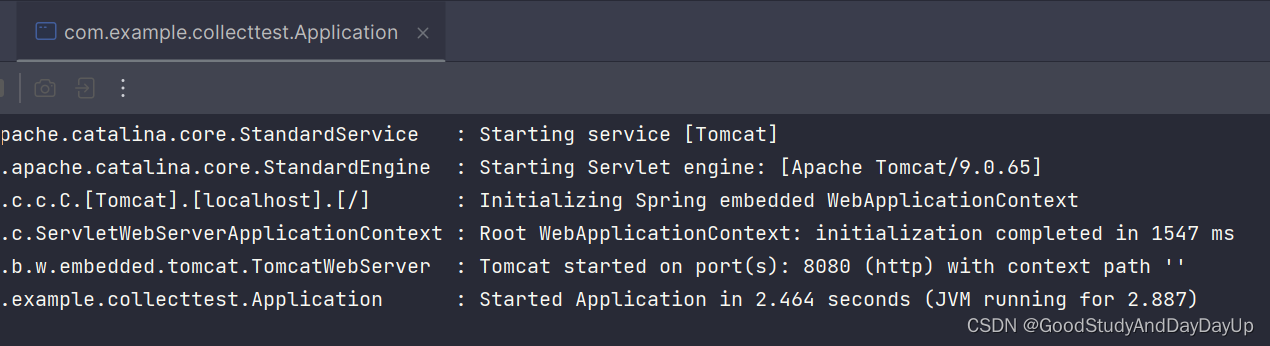
BF算法的特点是i回退，KMP算法的最大特点是i不回退，由于i不回退，所以KMP算法的时间复杂度是O(n+m)。

二.算法思想

在匹配主串和子串时，i指向主串，j指向子串，字符相等则i,j同时加1，当字符失配时，i不回退，j退到k的位置（相当必然有一段相同的路，那么相同的路i不走，等着j走过来即可）即相等的路j走过一段k长度的路。

三.公式证明

结论：

 在匹配成功的子串中找到两个最长的相等的真子串，这两个子串满足如下特点：

1. 一个串以子串的开头作为开头。
2. 另一个串以失配前的最后一个字符作为结尾()。
3. k正是子串的长度。

四.next数组及其练习

我们把所有位置的k值给保存在数组中，这个数组就是next数组。

1.

2.

 3.

4.

 五.找规律计算next[k]

例子：“abcabcdabcdabcdeabc”

不妨假设next[j]=k;

已知：next[1]=0,next[0]=-1;

由next[j]=k,得到  (1)

如果   (2)

(1)+(2)=

得到next[j+1]=k+1;

如图k=3

如果

又变成了一个模式匹配的问题，那么k=next[k];如图k=next[3]=0;

KMP最大特点是指示主串的指针不需要回溯，整个匹配过程中，对主串仅需从头到尾扫描一遍，这对处理从外设输入的庞大文件很有效，可以边读入边匹配，而无需回头重读。

六.代码实现

static int* GetNext(const char* str)
{
	int len = strlen(str);
	int* next = (int*)malloc(sizeof(int) * len);
	next[0] = -1;//不能再退
	next[1] = 0;//j=1,k=0;

	int j = 1;
	int k = 0;
	while (j+1 < len)
	{
		if ((k==-1)||str[k] == str[j])
		{
			next[++j] = ++k;
			/*next[j + 1] = k + 1;
			j += 1;
			k += 1;*/
		}
		else
		{
			k = next[k];
		}
	}
	return next;
}

int KMP(const char* str, const char* sub, int pos)
{
	assert(str != NULL && sub != NULL);
	if (str == NULL || sub == NULL || pos<0 || pos>strlen(str))
		return -1;

	int i = pos;
	int j = 0;
	int lenstr = strlen(str);
	int lensub = strlen(sub);
	int* next=GetNext(sub);
	//while (str[i] != '\0' && sub[j] != '\0')
	while (i < lenstr && j < lensub)
	{
		if ((j==-1)||str[i] == sub[j])
		{
			i++;
			j++;
		}
		else
		{
			//i不回退
			j = next[j];
		}
	}
	free(next);
	//判断是否查找成功，利用子串是否遍历完成，来判断是否查找成功
	//if (sub[j] == '\0')
	if (j >= lensub)
		return i - j;
	else
		return -1;
}

int main()
{
	const char* str1 = "ababcabcdabcde";
	const char* str2 = "abcd";

	printf("%d\n", KMP(str1, str2, 0));
	printf("%d\n", KMP(str1, str2, 6));
	printf("%d\n", KMP(str1, str2, 10));

	return 0;
}