目录
前言
一、题目
二、解题思路
1.直接查找
2.二分法
三、输出结果
前言
最近在牛客网刷题,刷到二维数组的查找,在这里记录一下做题过程
一、题目
描述
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
[
[1,2,8,9],
[2,4,9,12],
[4,7,10,13],
[6,8,11,15]
]
给定 target = 7,返回 true。
给定 target = 3,返回 false。
二、解题思路
1.直接查找
看到题目的时候第一时间是直接遍历整个二维数组查找,这个方法比较简单,但是时间复杂度比较高,最坏的情况下要遍历数组里的所有数据。
代码如下:
#include<iostream>
#include<math.h>
#include<vector>
using namespace std;
class Solution {
public:
bool Find(int target, vector<vector<int> > array) {
// 判断数组是否为空
int m = array.size();
if (m == 0) return false;
int n = array[0].size();
if (n == 0) return false;
int r = 0, c = n - 1; // 右上角元素
while (r < m && c >= 0) {
if (target == array[r][c]) {
return true;
}
else if (target > array[r][c]) {
r++;
}
else {
c--;
}
}
return false;
}
};
int main()
{
vector<vector<int> > array = { {1,2,3,4,5,6,7,8,9},{11,12,13,14,15,16,17,18,19},{20,21,22,23,24,25,26,27,28,29} };
Solution test;
bool result = test.Find(6, array);
std::cout << result << " " << std::endl;
return 0;
}
2.二分法
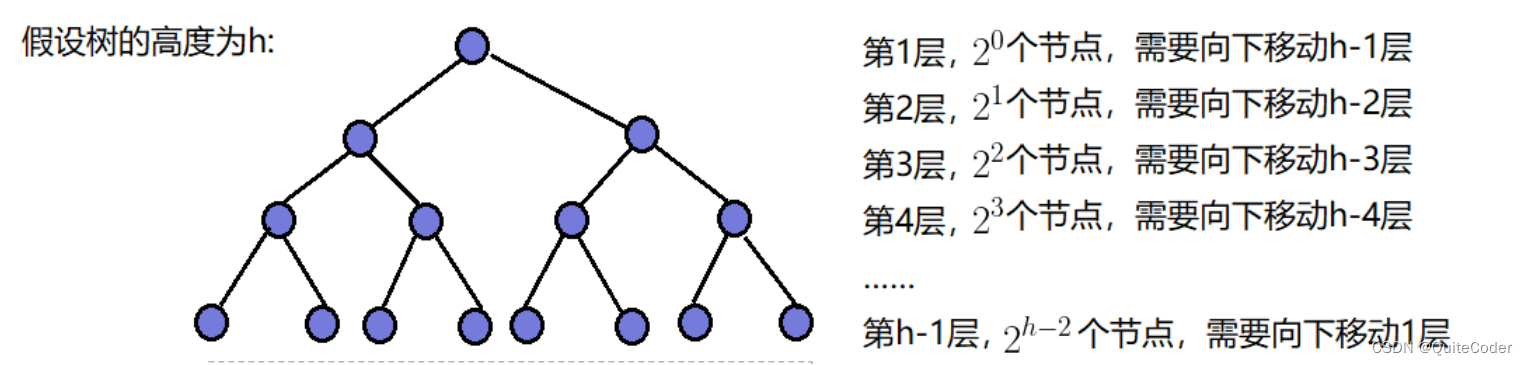
我们注意到,题目给出的数组从左到右递增,从上到下递增。如果简单查找,并没有用完题目中的提示。数据有序,所以我想到了二分法。
改进后的时间复杂度:O(m+n)
分析:

三、输出结果