朋友们大家好，本节内容来到堆的应用：堆排序和topk问题

我们在c语言中已经见到过几种排序，冒泡排序，快速排序（qsort）

冒泡排序的时间复杂度为O(N²),空间复杂度为O(1)；qsort排序的时间复杂度为
O(nlogn),空间复杂度为O(logn)，而今天所讲到的堆排序在时间与空间复杂度上相比于前两种均有优势

堆排序可以在原数组上进行，其空间复杂度为O(1);
堆排序提供了稳定的 (O(nlogn)) 时间复杂度

接下来我们进行讲解

首先我们来看这组代码：

int main()
{
	int a[] = { 6,3,5,7,11,4,9,13,1,8,15 };
	Heap hp;
	HeapInit(&hp);
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		HeapPush(&hp, a[i]);
	}
	while (!HeapEmpty(&hp))
	{
		printf("%d ", HeapTop(&hp));
		HeapPop(&hp);
	}
	printf("\n");

	return 0;

}

上节课我们知道，hp这个堆里面，a[i]并不一定是有序的

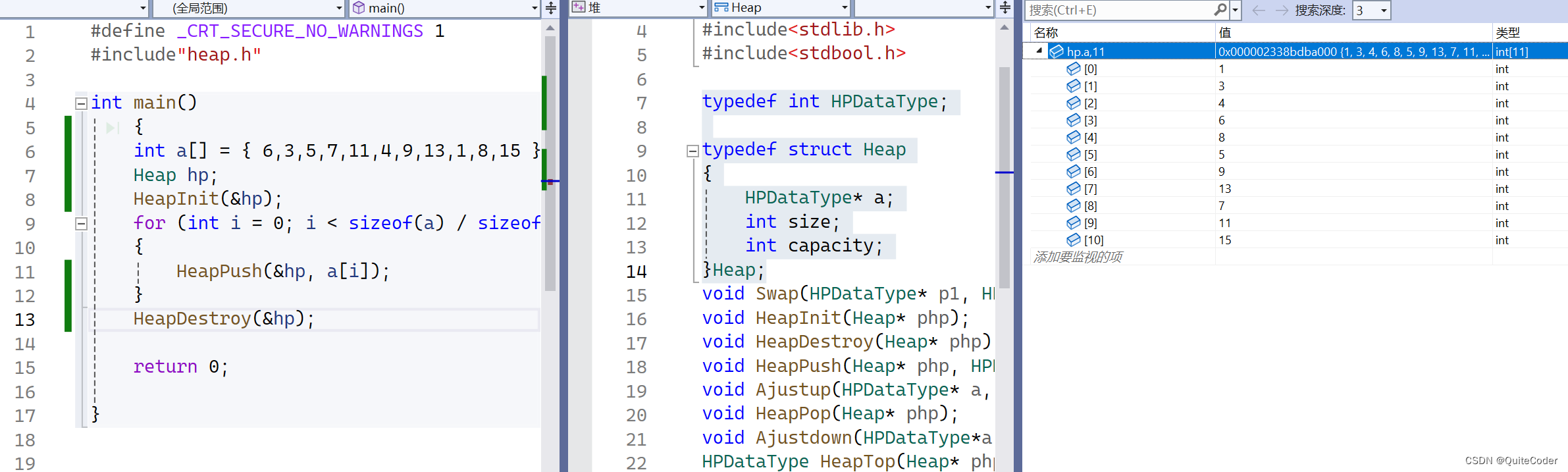
这里我们每次打印首元素，即最小元素，再删除掉，下一次获得到的堆顶元素仍为最小的，所以打印出来结果为有序的。但这个并不是堆排序，他只是每次获取堆顶最小元素

堆排序是直接在数组上实现的

1.堆排序的实现

堆排序的实现可以分为两部分：构建最大堆（或最小堆）和执行排序过程

首先我们来看建堆过程：

在上述代码中，我们是通过HeapPush(&hp, a[i]);来实现堆的插入，推其本质，是每次插入元素后进行向上调整，我们构建一个堆排序函数，其参数为传入的数组，和数组的元素个数：

void HeapSort(HPDataType* a, int n);

首先建堆，这里我们用向上调整建堆，在文章末尾会给大家引入向下调整建堆

for (int i = 1; i < n; i++)
{
	Ajustup(a, i);
}

从第二个元素开始，每次向上调整，完成堆的构建

建好之后我们则需要排序

1.1排序

思考一下，如果我们想要进行升序排序，需要建立大堆还是小堆呢？

在上述示例中，如果我们想进行升序，该怎么操作？？？

这里，如果我们想要升序排序，则需要建立大堆

小堆如果我们想要升序，堆顶元素在对应位置，剩余元素重新建立小堆，则时间复杂度大大增加

上述示例中，我们建了一个小堆，可以将Ajustup父节点与子节点大小关系改变来建立为大堆：

那思考一下，建立了大堆，我们如何实现升序呢？

这里我们就需要与删除堆顶元素相同的思路

1. 排序过程
   在大堆构建完成后，数组的根节点（即数组的第一个元素）是当前堆中的最大元素。通过将它与堆的最后一个元素交换，然后减少堆的大小（实际上是忽略数组的末尾元素），可以确保最大元素位于数组的正确位置上。

2. 调整堆
   交换根节点和最后一个节点之后，新的根节点可能破坏了大堆的性质，因此需要进行调整。调整的方法是将新的根节点“下沉”，直到恢复大堆的性质。

3. 重复过程
   重复对堆顶元素进行移除并调整堆的过程，直到堆的大小减少到1。在每一次重复过程中，都会将当前的最大元素放置到它在数组中的最终位置上。

所以我们代码实现就两步：

• 交换首尾元素
• 向下调整

void HeapSort(HPDataType* a, int n)
{
	//建堆
	for (int i = 1; i < n; i++)
	{
		Ajustup(a, i);
	}
	while (n>1)
	{
		Swap(&a[0], &a[n - 1]);
		n--;
		Ajustdown(a, n, 0);
	}
}

我们进行代码测试

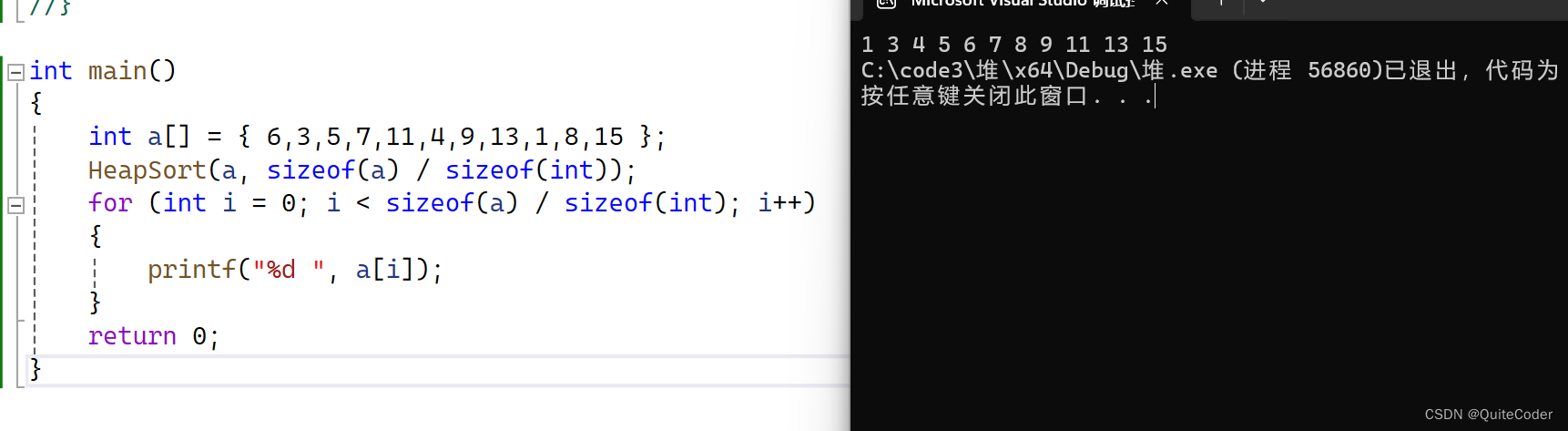
所以，堆这里可以促进我们快速选数，它的本质是选择排序

2.TOP-K问题

TOP-K问题指的是从一个大规模的数据集中找出“最重要”或“最优”的K个元素的问题，对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决

思路如下：

1. 用数据集合中前K个元素来建堆
   • 前k个最大的元素，则建小堆
   • 前k个最小的元素，则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

基于已经提供的堆操作函数，我们可以实现一个特定的PrintTopK函数，其目的是从数组a中找到最大的k个元素。

实现这一目标的思路是：

• 首先，使用数组a中的前k个元素建立一个最小堆。
• 然后，遍历剩余的n-k个元素。对于每个元素，如果它大于堆顶元素，则用它替换堆顶元素，然后对堆顶元素进行向下调整以维护最小堆的性质。
• 遍历完成后，堆中的k个元素即为整个数组中最大的k个元素。

void PrintTopK(int* a, int n, int k)
{
    Heap php;
    HeapInit(&php);
    
    for (int i = 0; i < k; ++i) {
        HeapPush(&php, a[i]);
    }
    for (int i = k; i < n; ++i) {
        if (a[i] > HeapTop(&php)) { // 如果当前元素比堆顶大
            HeapPop(&php); // 移除堆顶
            HeapPush(&php, a[i]); // 将当前元素加入堆中
        }
    }
    
    // 打印堆中的元素，即TOP K元素
    for (int i = 0; i < k; ++i) {
        printf("%d ", php.a[i]);
    }
    printf("\n");
    HeapDestroy(&php);
}

1. 用a中前k个元素建立堆
2. 将剩余n-k个元素与堆顶比较，替换并调整

测试代码：

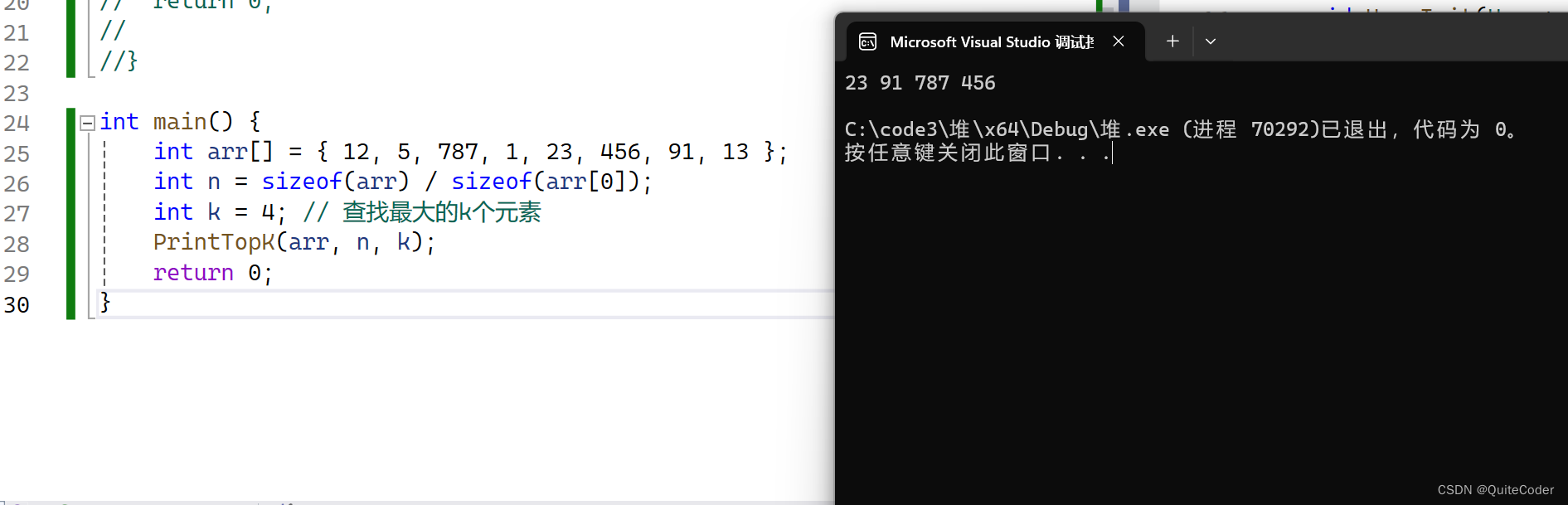
3.向上调整建堆与向下调整建堆

对于数组a，进行向上调整建堆：

for (int i = 1; i < n; i++)
{
	Ajustup(a, i);
}

要通过向下调整的方式建立堆，我们通常是从最后一个非叶子节点开始，逐层向上进行调整，这能保证每个子树都满足堆的性质

for (int i = n/2 - 1; i >= 0; i--) {
        AdjustDown(a, n, i);
    }

3.1对比两种方法的时间复杂度

向下调整建堆：

这个方法从最后一个非叶子节点开始，逆序对数组中的元素执行向下调整的操作。每个节点需要执行的向下调整操作取决于其高度，而数组中大约一半的节点是叶子节点，它们不需要被向下调整。对于剩下的节点，只有很少的节点需要移动到树的较低层次。具体地说，树的每一层上的节点数量减半，而向下移动的最大深度从0开始线性增加。

for (int i = n/2 - 1; i >= 0; i--) {
    AdjustDown(a, n, i);
}

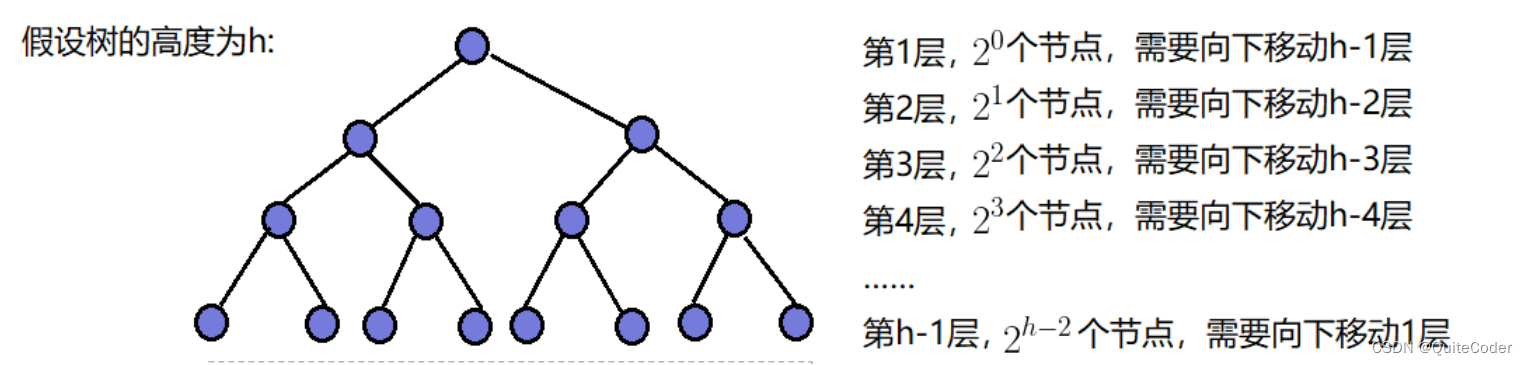
设向下调整的累计次数为T(h).

• 倒数第二层调整次数：2^h-2*1
• 倒数第三层调整次数：2^h-3*2
• ……
• 第一层调整次数：2⁰*(h-1);

对其进行累加和：

为等差×等比求和，通过错位相减则可求出结果：

T(h)=2^h-1-h;
h=log (n+1);

T(n)=n-log(n+1)

导致最大影响的项为n
所以向下调整的时间复杂度为O(N）

向上调整建堆

从第二层开始向上调整：

• 第二层调整次数：2¹*1
• 第三层调整次数：2²*2;
• 倒数第二层：2^h-2*(h-2);
• 倒数第一层：2^h-1*(h-1);

向上调整建堆

对于一个节点来说，向上调整可能需要比较和移动直到它的根节点，这在最坏的情况下是树的高度，对于一个完全二叉树来说，树的高度是 $O(\log n)$。对于代码段：

for (int i = 1; i < n; i++) {
    AdjustUp(a, i);
}

这个方法从第二个元素开始，逐一对数组中的元素执行向上调整的操作。对于数组中的第i个元素，最坏情况下向上调整操作需要沿着一条从叶节点到根节点的路径移动，路径的长度大约等于树的高度$h$，即 $O(\log i)$。因此，对于所有元素的总时间复杂度为：

$$T(n)=\sum _{i=1}^{n}O(\log i)=O(\log n!)=O(n\log n)$$

使用斯特灵公式($n!\approx \sqrt{2\pi n}(\frac{n}{e}{)}^n$)，可以推导出 $O(\log n!)$ 的大致等于 $O(n\log n)$，所以向上调整建堆的时间复杂度大约为 $O(n\log n)$。

向上调整建堆的时间复杂度是 $O(n\log n)$，而向下调整建堆的时间复杂度是 $O(n)$。因此，对于从零开始构建堆的场景，通常更倾向于使用向下调整的方法，因为它更加高效。

本节内容到此结束！感谢大家支持！