做仿真时经常使用到随机数，下面是一个场景：使用np.random.choice([0,1],p=[0.5,0.5],size=1)去进行随机的二选一，假设需要随机选择1000次，为了保证结果的稳健性，对前述过程重复50次，为了保证可复现性，对每次重复给予特定的随机数种子，即第n次重复时，设置np.random.seed(n)。我想观察的是1000次随机选择是否存在偏误（倾向于某个选项），因此我对1000次随机选择的结果求平均值，平均值低于0.5表明偏向于选项0，高于0.5表明偏向于选项1。下面是上述过程的实现：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
fig=plt.figure(figsize=(10,7))
xlist=[]
nxlist=[]
for n in range(50):
    np.random.seed(n)
    for i in range(1000):
        x=np.random.choice([0,1],p=[0.5,0.5],size=1)
        xlist.append(x)
    nxlist.append([n,np.mean(xlist)])
nxlist=pd.DataFrame(nxlist,columns=['n','xmean'])
plt.scatter(nxlist['n'], nxlist['xmean'])
plt.plot(nxlist['n'], [0.5]*len(nxlist['n']),color='red')

结果如下：

也就是说在1000次使用np.random.choice([0,1],p=[0.5,0.5],size=1)随机选择的过程中，选择更偏向于选项0，且以0-50为随机数种子的重复实验中基本都偏向于第一个选项。

为了检验随机数的收敛性，不再设置具体的随机数种子，使用系统时间这一默认随机数种子，重复随机选择10000次。以下是对应代码：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
fig=plt.figure(figsize=(10,7))
xlist=[]
for n in range(1):
    ixlist=[]
    for i in range(10000):
        x=np.random.choice([0,1],p=[0.5,0.5],size=1)
        xlist.append(x)
        ixlist.append([i,np.mean(xlist)])
ixlist=pd.DataFrame(ixlist,columns=['i','xmean'])
plt.scatter(ixlist['i'], ixlist['xmean'])
plt.plot(ixlist['i'], [0.5]*len(ixlist['i']),color='red')
plt.show()

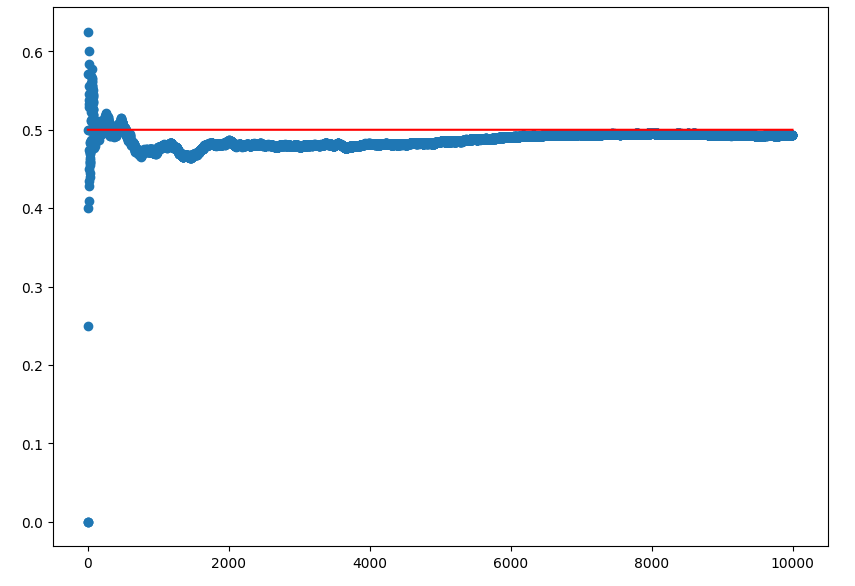
发现这个收敛性着实有点问题。所以建议做仿真算力够还是尽量多重复一些吧。