一、思想

选择排序的原理与思想非常直观和简单，它通过不断地选择未排序部分的最小（或最大）元素，并将其放到已排序部分的末尾来实现排序。

具体来说，选择排序的过程可以分解为以下几个步骤：

1. 寻找最小（或最大）元素：从未排序的序列中找到最小（或最大）的元素。
2. 交换位置：将找到的最小（或最大）元素与序列中的第一个位置的元素进行交换。
3. 缩小未排序范围：将序列的第一个位置排除在未排序的范围之外，因为它已经被放置在正确的位置上了。
4. 重复过程：重复上述步骤，每次从未排序的部分中寻找最小（或最大）元素，然后将其放到已排序部分的末尾，直到所有元素都排序完毕。

选择排序的时间复杂度为O(n^2)，其中n是序列的长度。这是因为对于每个元素，我们都需要遍历剩余的未排序元素来找到最小（或最大）值。尽管它在算法效率上不是最优的，但由于其实现简单，对于小数据集或者基本有序的数据集，选择排序是一个不错的选择。

二、图解

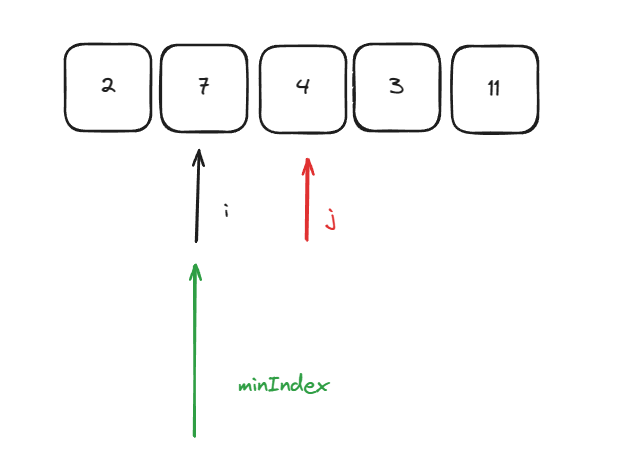
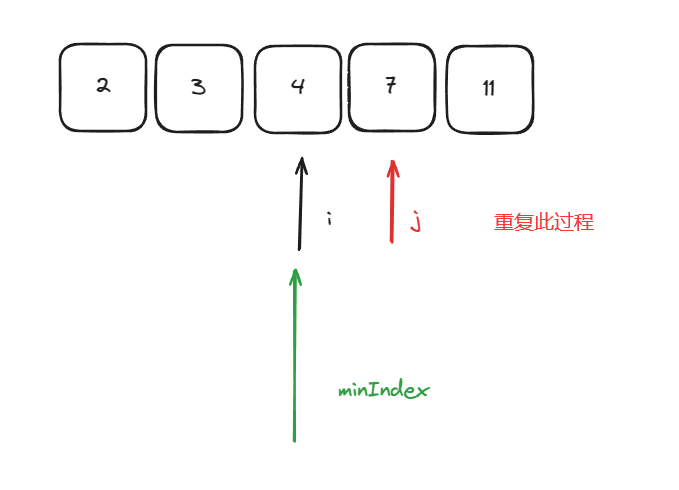
依旧将数组分为已排序部分跟为排序部分，初识时定义一个指针指向已排序部分的下一个位置，然后定义一个指针指向未排序部分，依次遍历未排序部分寻找未排序部分的最小值，寻找到后与已排序部分的下一个位置进行交换依次重复。开始时i指向已排序部分的下一个位置，j指针在未排序部分寻找最小值

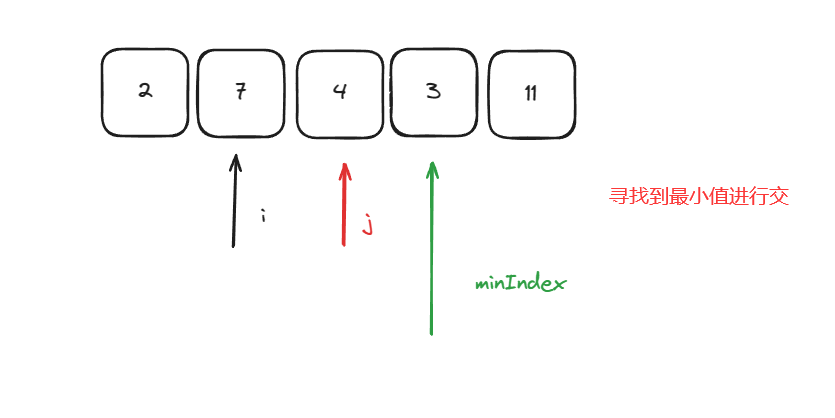
此时minIndex指向了最小值，于是将他与i位置进行交换，之后i指向下一个位置，j依旧在剩余未排序部分去寻找最小值，重复上述步骤

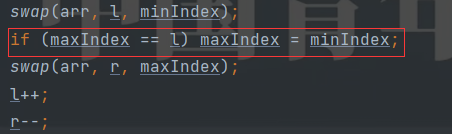
我们也可以进行优化，找一个是找要两个也是找，将数组整个分为三段[0,l -1]（前已排序部分）, [l, r]（未排序部分）, [r+1, n]（后已排序部分）我们可以同时在未排序部分寻找未排序部分的最小值和最大值，最小值与l交换,最大值与r交换，这里要注意的时在将最小值与l交换后，需要判断我们寻找到的最大值是否指向l，如果指向l，在前面最小值与l交换中，l指向的位置已经被交换到了minIndex位置，此时我们需要将maxIndex的位置进行修改，确保最大值不变

三、代码实现

寻找最小值

    public static void selectSort(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            int minIndex = i;
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[j] < arr[minIndex]) {
                    minIndex = j;
                }
            }
            swap(arr, i, minIndex);
        }
    }

同时寻找最大值与最小值

void select_sort(vector<int>& arr) {
    int l = 0, r = arr.size() - 1;
    while (l < r) {
        int minIndex = l, maxIndex = r;
        for (int i = l; i <= r; i++) {
            if (arr[i] < arr[minIndex]) minIndex = i;
            if (arr[i] > arr[maxIndex]) maxIndex = i;
        }
        swap(arr[l], arr[minIndex]);
        if (maxIndex == l) swap(arr[r], arr[minIndex]);
        else swap(arr[maxIndex], r);
        l++, r--;
    }
}

public static void selectSort(int[] arr) {
    int l = 0, r = arr.length - 1;
    while (l < r) {
        int minIndex = l, maxIndex = r;
        for (int i = l; i <= r; i++) {
            if (arr[i] > arr[maxIndex]) {
                maxIndex = i;
            }
            if (arr[i] < arr[minIndex]) {
                minIndex = i;
            }
        }
        swap(arr, l, minIndex);
        if (maxIndex == l) maxIndex = minIndex;
        swap(arr, r, maxIndex);
        l++;
        r--;
    }
}