所谓过拟合即模型复杂度较高,但用于训练数据集过于简单,最后导致模型将过多无用渣质作为学习对象
这个在上篇 深度学习_15_过拟合&欠拟合 已经详细介绍,以下便不再赘述。
上篇提到要想解决过拟合现象可以试着降低模型复杂度,又或者用复杂度匹配的数据集训练模型,但是数据集一般都是采集好的,无法更改,更改模型复杂度又可能涉及到更改模型本身,所以为了解决上述困扰,这里使用权重衰退方式调整模型,以达到让模型正常拟合
本次调整的代码对象仍是上篇实例代码
理论:

权重衰退采用限制模型本身w的数据取值范围,使模型的参数平方和小于θ,从而使模型的损失降低,从而限制模型的复杂度
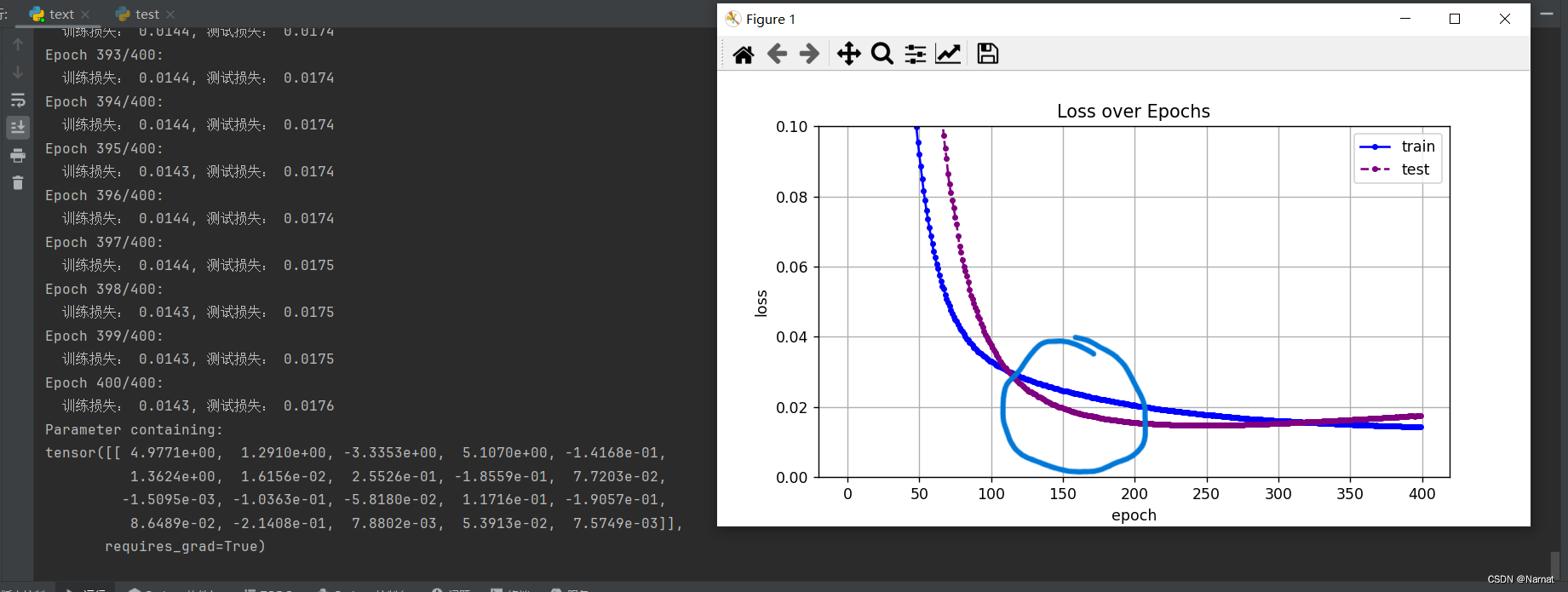
上篇提到过测试集合的损失在达到低谷后又会反弹,这是模型过拟合的表现,原因就是模型学习了其他的杂质,而我们利用上述权重衰退使得模型的参数平方和小于θ,这样模型想去学习新的参数,就会受到这个θ大小的限制,导致其无法学习新的θ,从而模型的大小被我们限制了起来,而杂质部分参数都会以0呈现,也就是模型前四个维度会趋近真正模型,后面杂质维度会趋近于0
θ大小也要把控好,若θ太小,模型会欠拟合
上述终究是理论,得用数学公式表示出来,也就等效于下方:

朴素的说下面两个公式等价

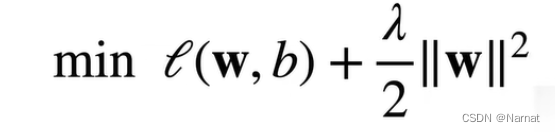
证明λ趋近0即相当于θ趋近无穷,对损失没有限制,λ趋近无穷则整体损失会变大,模型是往损失减小的方向学习,所以会间接导致w会变小,这与θ变小限制w的大小效果相同

实例代码:
对上篇代码增添了权重衰退法则,并写了两个不同的版本,两版本本质区别在于用了不同的优化模型手段,效果差别不大
版本1代码:
import math
import torch
from torch import nn
from d2l import torch as d2l
import matplotlib.pyplot as plt
# 生成随机的数据集
max_degree = 20 # 多项式的最大阶数
n_train, n_test = 100, 100 # 训练和测试数据集大小
true_w = torch.zeros(max_degree)
true_w[0:4] = torch.Tensor([5, 1.2, -3.4, 5.6])
# 生成特征
features = torch.randn((n_train + n_test, 1))
permutation_indices = torch.randperm(features.size(0))
# 使用随机排列的索引来打乱features张量(原地修改)
features = features[permutation_indices]
poly_features = torch.pow(features, torch.arange(max_degree).reshape(1, -1))
for i in range(max_degree):
poly_features[:, i] /= math.gamma(i + 1)
# 生成标签
labels = torch.matmul(poly_features, true_w)
labels += torch.normal(0, 0.1, size=labels.shape)
def evaluate_loss(net, data_iter, loss):
metric = d2l.Accumulator(2)
for X, y in data_iter:
out = net(X)
y = y.reshape(out.shape)
l = loss(out, y)
metric.add(l.sum(), l.numel())
return metric[0] / metric[1]
def l2_penalty(w):
w = w[0].weight
return torch.sum(w.pow(2)) / 2
# 修改后的训练函数
def train(train_features, test_features, train_labels, test_labels, lambd,
num_epochs=400):
loss = nn.MSELoss() # 损失函数
input_shape = train_features.shape[-1]
net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))
batch_size = min(10, train_labels.shape[0])
train_iter = d2l.load_array((train_features, train_labels.reshape(-1, 1)),
batch_size)
test_iter = d2l.load_array((test_features, test_labels.reshape(-1, 1)),
batch_size, is_train=False)
trainer = torch.optim.SGD(net.parameters(), lr=0.01, weight_decay=lambd) # 优化器调整模型
# 用于存储测试损失的列表
test_losses = []
train_losses = []
total_loss = 0
total_samples = 0
for epoch in range(num_epochs):
for X, y in train_iter:
trainer.zero_grad() # 删除之前的梯度
out = net(X)
l = loss(out, y) + lambd * l2_penalty(net)
l.backward() # 将梯度传递回模型
trainer.step() # 梯度更新
total_loss += l.sum().item() # 统计所有元素损失
total_samples += y.numel() # 统计个数
# 将当前的损失值添加到列表中
a = total_loss / total_samples # 本次训练的平均损失
train_losses.append(a) # 存
test_loss = evaluate_loss(net, test_iter, loss) # 本次训练的测试损失
test_losses.append(test_loss)
total_loss = 0
total_samples = 0
print(f"Epoch {epoch + 1}/{num_epochs}:")
print(f"训练损失: {a:.4f} 测试损失: {test_loss:.4f}")
# print(f" 训练损失: 测试损失: {loss(out, y):.4f}")
print(net[0].weight)
# 假设 test_losses 是已经计算出的测试损失值列表
plt.figure(figsize=(10, 6))
plt.plot(train_losses, label='train', color='blue', linestyle='-', marker='.')
plt.plot(test_losses, label='test', color='purple', linestyle='--', marker='.')
plt.xlabel('epoch')
plt.ylabel('loss')
plt.title('Test Loss over Epochs')
plt.legend()
plt.grid(True)
plt.ylim(0, 1) # 设置y轴的范围从0.01到100
plt.show()
# 选择多项式特征中的前4个维度
train(poly_features[:n_train, :4], poly_features[n_train:, :4],
labels[:n_train], labels[n_train:], 0)
版本2代码:
import math
import torch
from torch import nn
from d2l import torch as d2l
import matplotlib.pyplot as plt
# 生成随机的数据集
max_degree = 20 # 多项式的最大阶数
n_train, n_test = 100, 100 # 训练和测试数据集大小
true_w = torch.zeros(max_degree)
true_w[0:4] = torch.Tensor([5, 1.2, -3.4, 5.6])
# 生成特征
features = torch.randn((n_train + n_test, 1))
permutation_indices = torch.randperm(features.size(0))
# 使用随机排列的索引来打乱features张量(原地修改)
features = features[permutation_indices]
poly_features = torch.pow(features, torch.arange(max_degree).reshape(1, -1))
for i in range(max_degree):
poly_features[:, i] /= math.gamma(i + 1)
# 生成标签
labels = torch.matmul(poly_features, true_w)
labels += torch.normal(0, 0.1, size=labels.shape)
# 以下是你原来的训练函数,没有修改
def evaluate_loss(net, data_iter, loss):
metric = d2l.Accumulator(2)
for X, y in data_iter:
out = net(X)
y = y.reshape(out.shape)
l = loss(out, y)
metric.add(l.sum(), l.numel())
return metric[0] / metric[1]
def l2_penalty(w):
w = w[0].weight
return torch.sum(w.pow(2)) / 2
def train(train_features, test_features, train_labels, test_labels, lambd,
num_epochs=400):
loss = d2l.squared_loss
input_shape = train_features.shape[-1]
net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))
batch_size = min(10, train_labels.shape[0])
train_iter = d2l.load_array((train_features, train_labels.reshape(-1, 1)),
batch_size)
test_iter = d2l.load_array((test_features, test_labels.reshape(-1, 1)),
batch_size, is_train=False)
# 用于存储训练和测试损失的列表
train_losses = []
test_losses = []
total_loss = 0
total_samples = 0
for epoch in range(num_epochs):
for X, y in train_iter:
out = net(X)
l = loss(out, y) + lambd * l2_penalty(net)
# 反向传播和优化器更新
l.sum().backward()
d2l.sgd(net.parameters(), lr=0.01, batch_size= batch_size)
total_loss += l.sum().item() # 统计所有元素损失
total_samples += y.numel() # 统计个数
a = total_loss / total_samples # 本次训练的平均损失
train_losses.append(a)
test_loss = evaluate_loss(net, test_iter, loss)
test_losses.append(test_loss)
total_loss = 0
total_samples = 0
print(f"Epoch {epoch + 1}/{num_epochs}:")
print(f"训练损失: {a:.4f} 测试损失: {test_loss:.4f} ")
print(net[0].weight)
# 绘制损失曲线
plt.figure(figsize=(10, 6))
plt.plot(train_losses, label='train', color='blue', linestyle='-', marker='.')
plt.plot(test_losses, label='test', color='purple', linestyle='--', marker='.')
plt.xlabel('epoch')
plt.ylabel('loss')
plt.title('Loss over Epochs')
plt.legend()
plt.grid(True)
plt.ylim(0, 100) # 设置y轴的范围从0.01到100
plt.show()
# 选择多项式特征中的前4个维度
train(poly_features[:n_train, :4], poly_features[n_train:, :4],
labels[:n_train], labels[n_train:], 0)
代码分析:
def l2_penalty(w):
w = w[0].weight
return torch.sum(w.pow(2)) / 2
取模型参数平方和除以2
out = net(X)
l = loss(out, y) + lambd * l2_penalty(net)
# 反向传播和优化器更新
l.sum().backward()
d2l.sgd(net.parameters(), lr=0.01, batch_size= batch_size)
用模型算出结果,然后计算损失,算出梯度并返还到模型中,利用sgd优化算法,更新模型参数
没有用torch本身优化函数所以l.sum().backward()不能简写
其他不再赘述,上篇已经写的很明白了
过拟合:
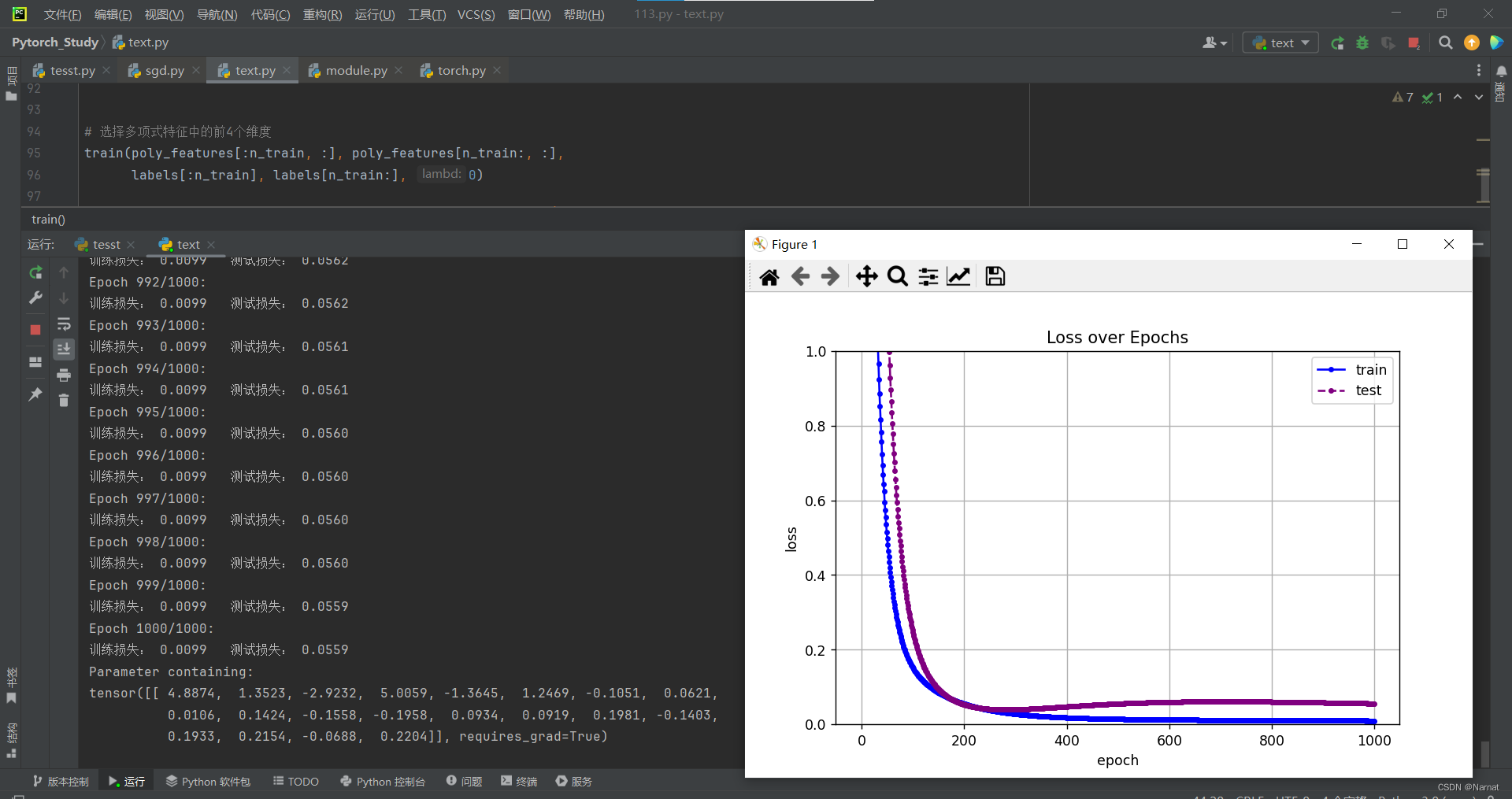
很明显测试集在损失达到最低后又上升,这是过拟合现象
利用权重衰退调整过拟合
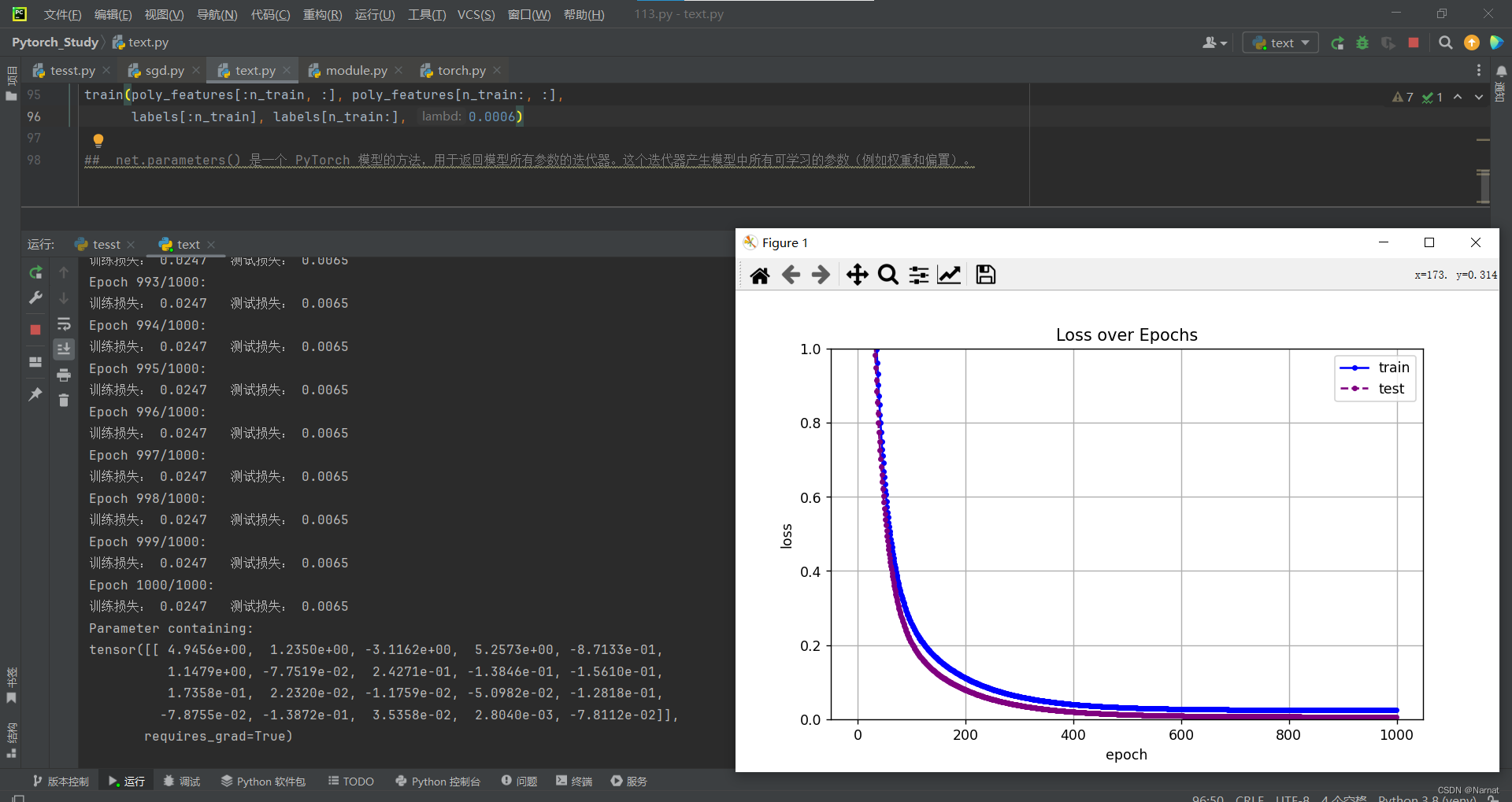
在上述过拟合条件下将λ设为0.006即可缓解过拟合现象
顺带提一下,train损失比test损失高出的部分有训练损失多加的lambd * l2_penalty(net)部分和loss(out, y)升高部分,总体来说是两者制衡效果的体现
正常拟合

可看出上述调整过后的过拟合test损失与正常拟合的test损失及其接近,说明调成效果不错