【LeetCode】升级打怪之路 Day 13：优先级队列的应用

news2024/10/5 16:19:54

今日题目：

23. 合并 K 个升序链表 | LeetCode
378. 有序矩阵中第 K 小的元素 | LeetCode
373. 查找和最小的 K 对数字 | LeetCode
703. 数据流中的第 K 大元素 | LeetCode
347. 前 K 个高频元素 | LeetCode

- Problem 1：合并多个有序链表【classic】
- - LC 23. 合并 K 个升序链表 ⭐⭐⭐⭐⭐
  - LC 378. 有序矩阵中第 K 小的元素
  - LC 373. 查找和最小的 K 对数字【略有难度】
- Problem 2：寻找第 k 个最大元素
- - LC 703. 数据流中的第 K 大元素【classic】 ⭐⭐⭐⭐⭐
  - LC 347. 前 K 个高频元素【easy】

优先级队列的特色是动态排序，插入的元素可以自动维护正确的顺序。其限制就是，优先级队列的限制是只能从队头和队尾操作元素。

一般来说，用到优先级队列的题目主要分两类：

一类是合并多个有序链表这类题
另一类是寻找第 k 个最大元素这类题

这两类题目都是经典题型，需要理解。

Problem 1：合并多个有序链表【classic】

有很多题目在使用优先级队列时，解题思路都可以归结于“合并多个有序链表”，这里先学会使用 PriorityQueue 来解决合并多个有序链表的问题，再看看有哪些变形。

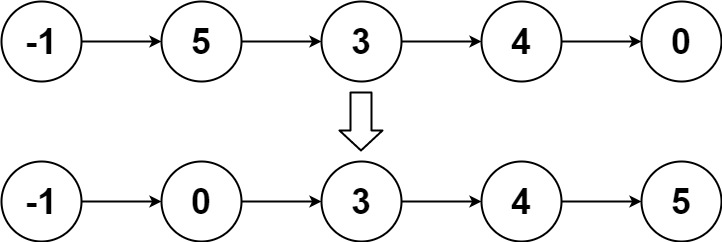
LC 23. 合并 K 个升序链表 ⭐⭐⭐⭐⭐

23. 合并 K 个升序链表 | LeetCode

这个题目可以用双指针法，但使用优先级队列更能解决这一大类问题。

这种题的基本思路就是：将每个链表的头节点入队，然后开始迭代，每轮迭代中，从队列中拿出堆顶元素（即最小元素），然后把这个节点的 next 节点入队，进入下一轮迭代。直到合并结束。

这种解题思路很巧妙地运用了各链表“升序”的特点以及优先级队列的好处。

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if (lists.length == 0) {
            return null;
        }
        
        PriorityQueue<ListNode> queue = new PriorityQueue<>(lists.length, (a, b) -> (a.val - b.val));
        ListNode vHead = new ListNode();
        ListNode curr = vHead;

        // 将各链表的头节点放入队列中
        for (var node: lists) {
            if (node != null) {
                queue.offer(node);
            }
        }

        while (!queue.isEmpty()) {
            var min = queue.poll();  // 获取当前堆中最小元素节点
            curr.next = min;
            curr = curr.next;
            if (min.next != null) {
                queue.offer(min.next);
            }
        }

        return vHead.next;
    }
}

LC 378. 有序矩阵中第 K 小的元素

378. 有序矩阵中第 K 小的元素 | LeetCode

这个题是上面“合并 K 个升序链表”的变形题，因为矩阵的每一行都是升序的，可以将矩阵的每一行视为一个升序链表，这样解题思路就与之前的是一样了，难度不大。

LC 373. 查找和最小的 K 对数字【略有难度】

373. 查找和最小的 K 对数字 | LeetCode

一开始做这个题，没有想到如何使用 PriorityQueue，也没有将这个题转换到“合并 K 个升序链表”这个基本问题的思路上，导致出现多次提交错误。这个题目本质上还是合并 K 个升序链表的变形。

这个题目可以这样想象将其转换为 K 个有序链表：将固定一个 nums1[i] 与 nums2 的各个元素进行相加，就可以一串升序的结果。所以每个 nums1 的元素可以按照上面这种方式得到一个链表，那么这个问题就转换为了 nums1.length 个升序链表的合并问题了。

举例子可以参考 labuladong 的讲解：

在这里插入图片描述

想清楚思路之后，难度也就还行了。

Problem 2：寻找第 k 个最大元素

这是 PriorityQueue 的另一个经典应用。直接通过题目来看一下。

LC 703. 数据流中的第 K 大元素【classic】 ⭐⭐⭐⭐⭐

703. 数据流中的第 K 大元素 | LeetCode

这个题目是经典的利用 PriorityQueue 来寻找第 k 个最大元素的问题。

PriorityQueue 来寻找 Top K 的方法与排序等方法的关键区别在于：只找到 Top K，不排序 Top K。

因为如果使用排序法的话，就是对所有元素排序，然后就可以找到 top K 了，但是使用 priority queue 的话，Top K 的 K 个元素的顺序都是可以不用排出来的。

解题思路：

top-k

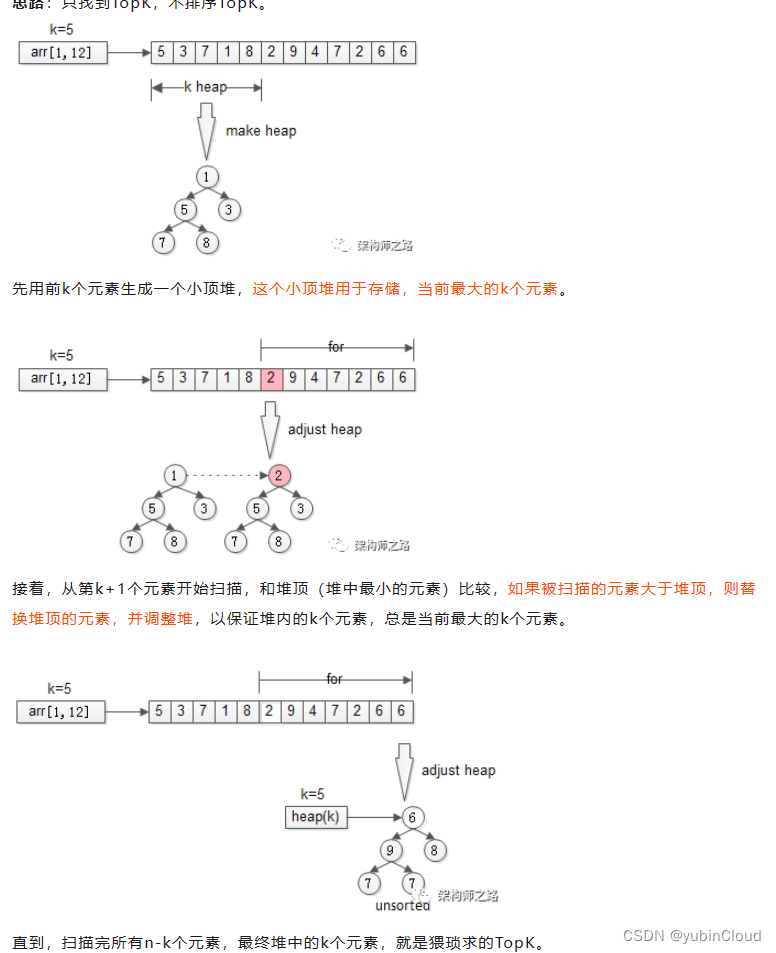
来源：拜托，面试别再问我TopK了！！！

这里可以得到一个经验：保持小根堆一直为 K 的元素，就可以保证这 K 个元素是一个数据流的最大的 K 的元素，因为比他们小的元素都被 pop 出去了，因为小根堆的顶端是最小元素，所以每次 pop 出去的一定是最小元素。

代码实现：

class KthLargest {

    private int k;

    private PriorityQueue<Integer> heap;

    public KthLargest(int k, int[] nums) {
        this.k = k;
        this.heap = new PriorityQueue<>(k + 1);
        for (int num: nums) {
            heap.offer(num);
            if (heap.size() > k) {
                heap.poll();  // pop 出最小元素
            }
        }
    }
    
    public int add(int val) {
        heap.offer(val);
        while (heap.size() > k) {
            heap.poll();  // pop 出最小元素
        }
        return heap.peek();  // 堆中是最大的 K 个元素，堆顶就是这个 K 个元素中最小的那个，也就是第 K 大的元素
    }
}