33、排序链表

给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

示例 1：

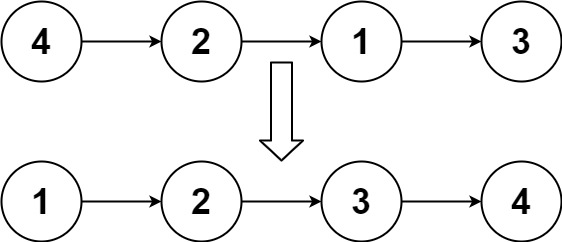
输入：head = [4,2,1,3]
输出：[1,2,3,4]

示例 2：

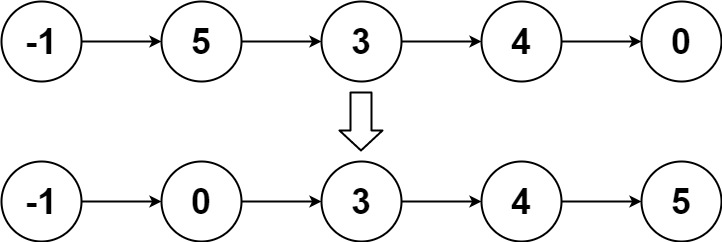
输入：head = [-1,5,3,4,0]
输出：[-1,0,3,4,5]

示例 3：

输入：head = []
输出：[]

提示：

• 链表中节点的数目在范围 [0, 5 * 104] 内
• -105 <= Node.val <= 105

思路解答：

1. 使用快慢指针找到链表的中点，将链表分为两部分。
2. 递归地对左右两部分链表进行排序。
3. 合并两个已排序的链表。

def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:
    if not head or not head.next:
        return head

    def getMiddle(head):
        slow = head
        fast = head

        while fast.next and fast.next.next:
            slow = slow.next
            fast = fast.next.next

        return slow

    def merge(left, right):
        dummy = ListNode(0)
        current = dummy

        while left and right:
            if left.val < right.val:
                current.next = left
                left = left.next
            else:
                current.next = right
                right = right.next
            current = current.next

        current.next = left if left else right

        return dummy.next

    # 获取链表中点，将链表分为两部分
    mid = getMiddle(head)
    left = head
    right = mid.next
    mid.next = None

    # 递归地对左右两部分链表进行排序
    left_sorted = sortList(left)
    right_sorted = sortList(right)

    # 合并两个已排序的链表
    return merge(left_sorted, right_sorted)

34、合并K个升序链表

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：

输入：lists = []
输出：[]

示例 3：

输入：lists = [[]]
输出：[]

提示：

• k == lists.length
• 0 <= k <= 10^4
• 0 <= lists[i].length <= 500
• -10^4 <= lists[i][j] <= 10^4
• lists[i] 按 升序 排列
• lists[i].length 的总和不超过 10^4

思路解答：

1. 初始化一个优先队列（heap）：首先，创建一个空的优先队列（heap），用于存储链表的头部节点。将每个链表的头部节点（值和节点本身的元组）加入到优先队列中，并根据节点的值进行排序。
2. 创建一个虚拟头节点和当前节点：创建一个虚拟头节点dummy和一个指向当前节点的指针curr，初始时它们都指向虚拟头节点。
3. 循环处理优先队列：在一个循环中，不断从优先队列中弹出最小的节点。将该节点接入到合并后的链表中，更新当前节点指针curr。如果被弹出的节点有下一个节点，则将下一个节点（值和节点本身的元组）重新加入到优先队列中。
4. 返回合并后的链表：最终，返回虚拟头节点的下一个节点，即为合并后的链表的头节点。

def mergeKLists(self, lists: list[Optional[ListNode]]) -> Optional[ListNode]:

    setattr(ListNode, "__lt__", lambda a, b: a.val < b.val)
    heap = []
    for l in lists:
        if l:
            heapq.heappush(heap, (l.val, l))  # 将节点的值和节点本身存入堆中

    dummy = ListNode(0)
    current = dummy

    while heap:
        val, node = heapq.heappop(heap)  # 从堆中取出节点的值和节点本身
        current.next = node
        current = current.next
        if node.next:
            heapq.heappush(heap, (node.next.val, node.next))  # 将下一个节点的值和节点本身存入堆中

    return dummy.next

35、LRU缓存

请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。

实现 LRUCache 类：

• LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
• int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
• void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：

输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

提示：

• 1 <= capacity <= 3000
• 0 <= key <= 10000
• 0 <= value <= 105
• 最多调用 2 * 105 次 get 和 put

思路解答：

1. 使用一个哈希表（dictionary）来存储key和对应的节点。
2. 使用一个双向链表来维护节点的访问顺序，链表头部表示最久未使用的节点，链表尾部表示最近访问的节点。
3. LRUCache类中包含get和put方法：
   • get(key)方法：
     • 如果key存在于缓存中，从哈希表中获取对应的节点，并将该节点移动到链表尾部表示最近访问。
     • 如果key不存在于缓存中，返回-1。
   • put(key, value)方法：
     • 如果key已存在于缓存中，更新对应节点的值，并将其移动到链表尾部表示最近访问。
     • 如果key不存在于缓存中：
       • 创建一个新节点，插入到链表尾部表示最近访问。
       • 将key和对应节点存入哈希表。
       • 如果插入操作导致缓存容量超过限制，移除链表头部节点，同时从哈希表中删除对应的键值对。

class ListNode:
    def __init__(self, key=0, val=0):
        self.key = key
        self.val = val
        self.prev = None
        self.next = None


class LRUCache:
    def __init__(self, capacity):
        self.capacity = capacity
        self.cache = {}
        self.head = ListNode()
        self.tail = ListNode()
        self.head.next = self.tail
        self.tail.prev = self.head

    def get(self, key):
        if key in self.cache:
            node = self.cache[key]
            self._remove(node)
            self._add(node)
            return node.val
        return -1

    def put(self, key, value):
        if key in self.cache:
            self._remove(self.cache[key])
        node = ListNode(key, value)
        self.cache[key] = node
        self._add(node)

        if len(self.cache) > self.capacity:
            node_to_remove = self.head.next
            self._remove(node_to_remove)
            del self.cache[node_to_remove.key]

    def _add(self, node):
        prev_node = self.tail.prev
        prev_node.next = node
        node.prev = prev_node
        node.next = self.tail
        self.tail.prev = node

    def _remove(self, node):
        prev_node = node.prev
        next_node = node.next
        prev_node.next = next_node
        next_node.prev = prev_node