一、变分推断简介

变分推理的目标是近似潜在变量(latent variables)在观测变量（observed variables）下的条件概率。解决该问题，需要使用优化方法。在变分推断中，需要使用到的一个重要理论，是平均场理论。

1、平均场理论

来源于物理学，是一种研究复杂多体问题的方法，将数量巨大的互相作用的多体问题转化成每一个粒子处在一种弱周期场中的单体问题。如果将其应用到图模型中，可以将相互作用的多体看成相互作用的变量：

2、变分贝叶斯推断

 3、变分贝叶斯推断

变分推断等价于最小化KL散度。

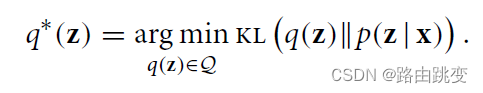
其中，q(z)为近似分布，p(z∣x)为所要求的的后验概率分布。这里之所以对 p(z|x)进行近似，是因为其很难计算，在下一小节将对其进行讨论。

KL散度可以表示为：

其中，Q(x)为要近似的分布，P(x∣D)为参数x的条件概率分布。

这个公式可以继续化简（见2、变分贝叶斯推断或者参考：A Tutorial on Variational Bayesian Inference），化简后的结果为：

其中，lnP(D)为log似然，L LL为log似然的下界。使得KL散度最小，相当于最大化L 。如下为三者之间的关系：

二、ELBO

ELBO，全称为 Evidence Lower Bound，即证据下界。这里的证据指数据或可观测变量的概率密度。

假设表示一系列可观测数据集，为一系列隐变量(latent variables)。则可用表示联合概率，为条件概率，为证据。

那么，贝叶斯推理需要求解的就是条件概率，即：

然而，对很多模型而言，计算是很困难的，即：

因此，无法直接计算。那么，这里变分推断就来了。在上一节中已提及，变分推断的目标是找到一个概率密度函数来近似，要得到最佳的必须优化：

其中，KL散度可以表示为：

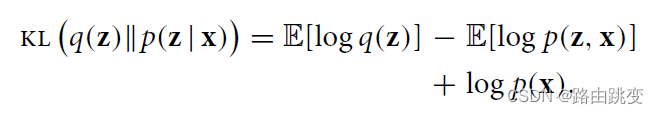
由于KL散度大于0，进而我们可以求得：

这里终于知道为什么叫证据下界了吧，即公式的左边的证据的对数形式，右边为其下界。因此，我们有：

在使用变分推断时，首先需要计算的便是ELBO。从上面的公式可以看到，要计算ELBO，需要写出联合概率密度和。

在写出这两个式子之后，带入ELBO公式，分别求对数。之后，分别求期望。在期望计算完之后，针对具体的变分参数，求偏导，并令偏导为0，即可得到变分参数的更新公式。

在实际公式推导过程中，关键点就在于如何求期望。其计算期望往往需要用到指数分布族的性质，即可以将期望计算转化成求导计算。

三、指数分布族(Exponential Family)相关公式推导及在变分推断中的应用

1、指数分布族的概念

指数分布族是一系列分布的统称，包含连续和离散的相关分布