【回溯算法】【回溯算法剪枝】 Leetcode 77.组合 216. 组合总和 III
- 回溯算法可以解决的问题
- Leetcode 77.组合
- 解法1 回溯法三部曲,函数参数、终止条件和单层搜索逻辑
- 解法一plus 回溯法+剪枝
- 另一道组合回溯问题 216. 组合总和 III
- 解法:回溯
- 解法: 回溯+剪枝
回溯算法可以解决的问题
组合问题:N个数里面按一定规则找出k个数的集合
切割问题:一个字符串按一定规则有几种切割方式
子集问题:一个N个数的集合里有多少符合条件的子集
排列问题:N个数按一定规则全排列,有几种排列方式
棋盘问题:N皇后,解数独等等

Leetcode 77.组合

---------------🎈🎈题目链接🎈🎈-------------------
解法1 回溯法三部曲,函数参数、终止条件和单层搜索逻辑
class Solution {
List<List<Integer>> result = new ArrayList<>(); // 用于汇总单一结果作为最终结果
List<Integer> path = new ArrayList<>(); // 用于存放符合条件单一结果
public List<List<Integer>> combine(int n, int k) {
backtracking(n,k,1);
return result;
}
public void backtracking(int n, int k, int startindex){ // 1.确定递归函数的参数和返回值
// 2.确定终止条件:当最后得到的path的大小等于k 就可以将path存入result中了 终止递归
// 注意一下!!这里把path存进result的时候,不能直接存path,不然就是浅拷贝,最后result中的值都一样
if(path.size() == k){
result.add(new ArrayList<>(path));
return;
}
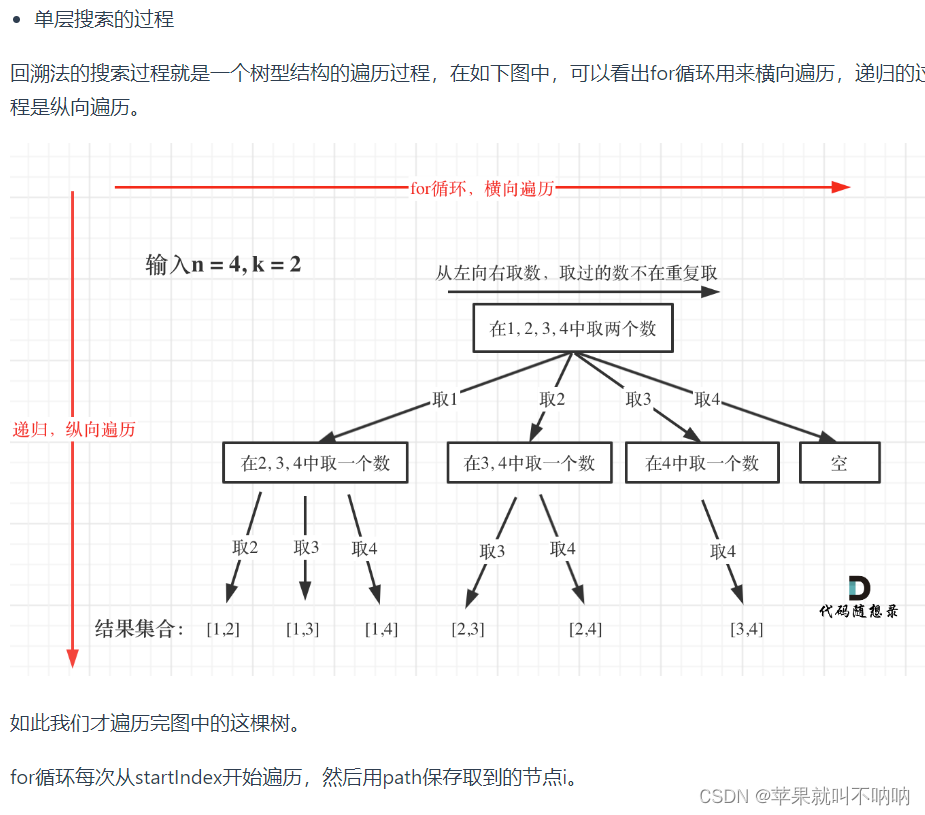
// 3. 确定横向的单层搜索逻辑 每次搜索都是从startindex开始,startindex保证取过不再取 保证【组合】
// for循环用来横向遍历,从左到右取数 取过的数字不再取。递归的过程是纵向遍历,下一层搜索要从i+1开始。
// 这里i<=n是因为 数据是范围 [1, n],i就代表了数据,而不是索引
for(int i = startindex; i <= n; i++){ // 控制树的横向遍历
path.add(i); // 处理节点:将i加入到path路径中
backtracking(n,k,i+1); // 递归:控制树的纵向遍历,注意下一层搜索要从startindex = i+1开始
path.removeLast(); // 回溯,撤销处理的节点
}
}
}
注意事项 ⭐️
注意浅拷贝和深拷贝:使用new ArrayList<>(path)
注意移除ArrayList的最后一个元素方法:path.removeLast()
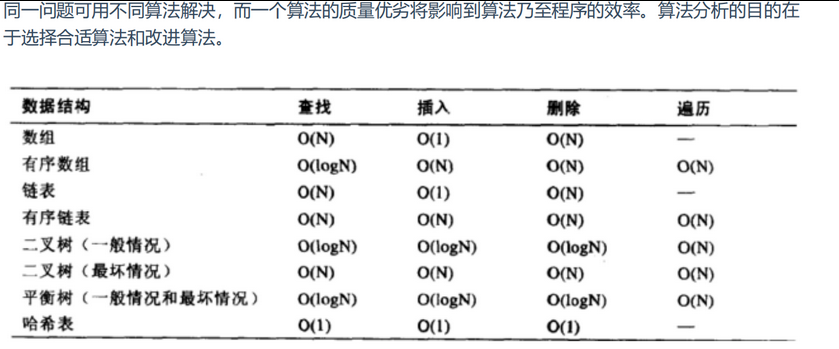
时间复杂度:分析回溯问题的时间复杂度,有一个通用公式:路径长度×搜索树的叶子数。对于本题它等于 O(k⋅C(n,k))
对于给定的n个元素,从中选择k个元素的组合数是C(n, k)。每个组合的平均长度是k(即组合中有k个元素),
空间复杂度:O(k),递归调用栈最大深度为k(k为要生成的组合的长度)
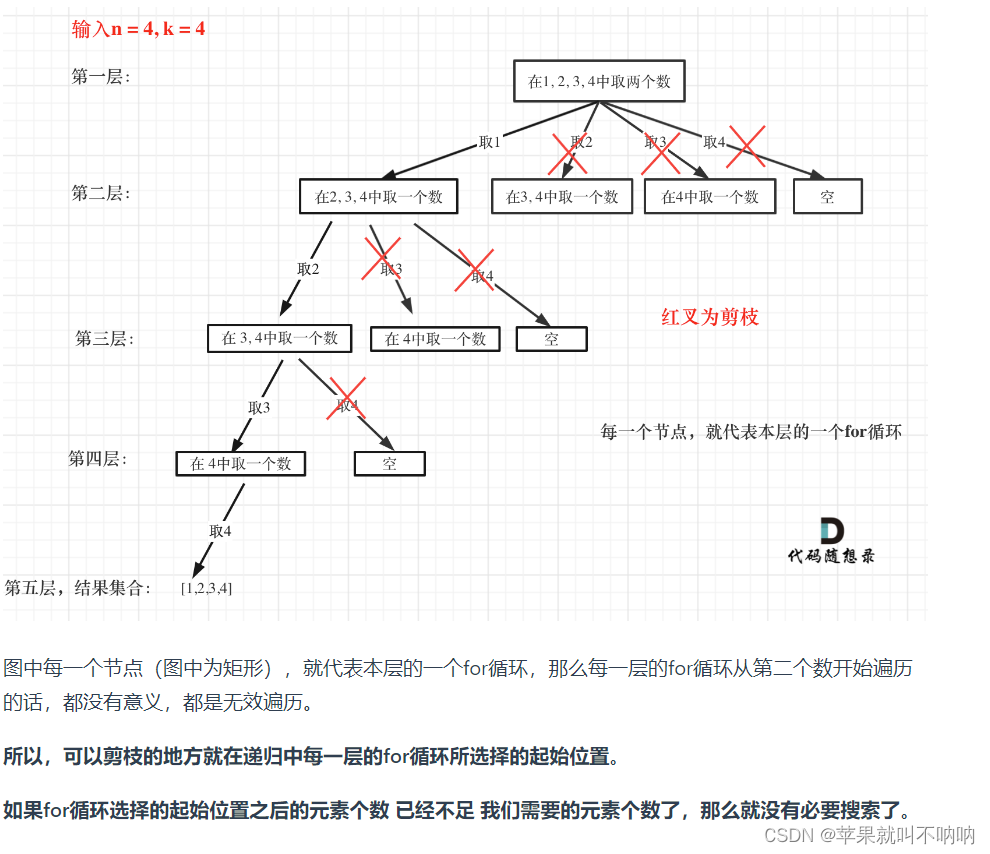
解法一plus 回溯法+剪枝
注意事项 ⭐️
注意浅拷贝和深拷贝:使用new ArrayList<>(path)
注意移除ArrayList的最后一个元素方法:path.removeLast()
剪枝优化:if(n-(i-startindex)<k) continue; // 剪枝操作自己写出来所有的变量,就知道了!!!要动手
class Solution {
List<List<Integer>> result = new ArrayList<>(); // 用于汇总单一结果作为最终结果
List<Integer> path = new ArrayList<>(); // 用于存放符合条件单一结果
public List<List<Integer>> combine(int n, int k) {
backtracking(n,k,1);
return result;
}
public void backtracking(int n, int k, int startindex){ // 1.确定递归函数的参数和返回值
// 2.确定终止条件:当最后得到的path的大小等于k 就可以将path存入result中了 终止递归
// 注意一下这里把path存进result的时候,不能直接存path,不然就是浅拷贝,最后result中的值都一样
if(path.size() == k){
result.add(new ArrayList<>(path));
return;
}
// 3. 确定横向的单层搜索逻辑 每次搜索都是从startindex开始,startindex保证取过不再取 保证【组合】
// for循环用来横向遍历,从左到右取数 取过的数字不再取。递归的过程是纵向遍历,下一层搜索要从i+1开始。
// 这里i<=n是因为 数据是范围 [1, n],i就代表了数据,而不是索引
for(int i = startindex; i <= n; i++){ // 控制树的横向遍历
if(n-(i-startindex)<k) continue; // 剪枝操作!!!!!!!!!!!!!!!!!!!!!!!!!!
path.add(i); // 处理节点:将i加入到path路径中
backtracking(n,k,i+1); // 递归:控制树的纵向遍历,注意下一层搜索要从startindex = i+1开始
path.removeLast(); // 回溯,撤销处理的节点
}
}
}
另一道组合回溯问题 216. 组合总和 III
相对于77. 组合 (opens new window),无非就是多了一个限制,本题是要找到和为n的k个数的组合,而整个集合已经是固定的了[1,…,9]。
本题k相当于树的深度,9(因为整个集合就是9个数)就是树的宽度。
例如 k = 2,n = 4的话,就是在集合[1,2,3,4,5,6,7,8,9]中求 k(个数) = 2, n(和) = 4的组合。
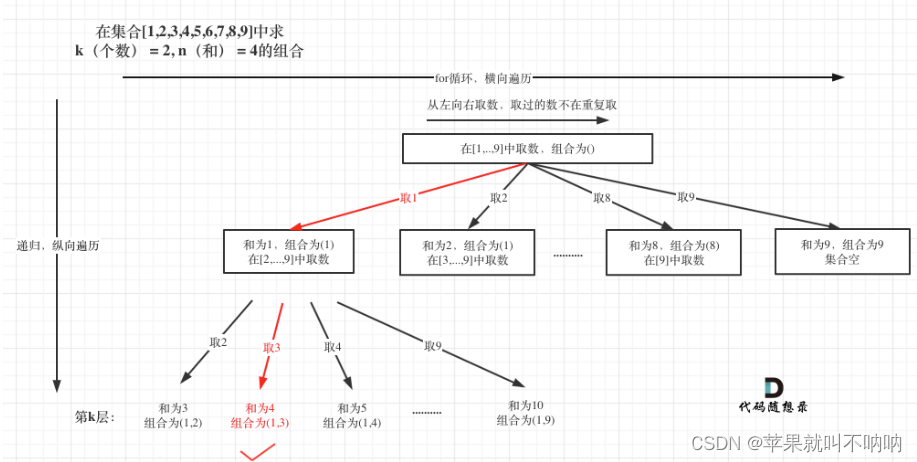
解法:回溯
遍历求加和sum,sum=n时,若递归深度为k,则将当前path加入result
if(sum == n){ if(path.size() == k){ result.add(new ArrayList<>(path)); // 注意新建ArrayList赋值!!!!!! } return; // 如果path.size() == k 但sum != targetSum 直接返回 }之后进行回溯,sum回溯+path回溯
class Solution {
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new ArrayList<>();
int sum = 0;
public List<List<Integer>> combinationSum3(int k, int n) {
backtracking(k,n,1);
return result;
}
public void backtracking(int k, int n, int startindex){
// 终止条件
if(sum == n){
if(path.size() == k){
result.add(new ArrayList<>(path));
}
return;
}
for(int i = startindex; i <= 9; i++){
path.add(i);
sum += i;
backtracking(k,n,i+1);
sum -= path.get(path.size()-1); // 回溯
//sum -= i; // 回溯 这个方法也行
path.removeLast(); // 回溯
}
}
}
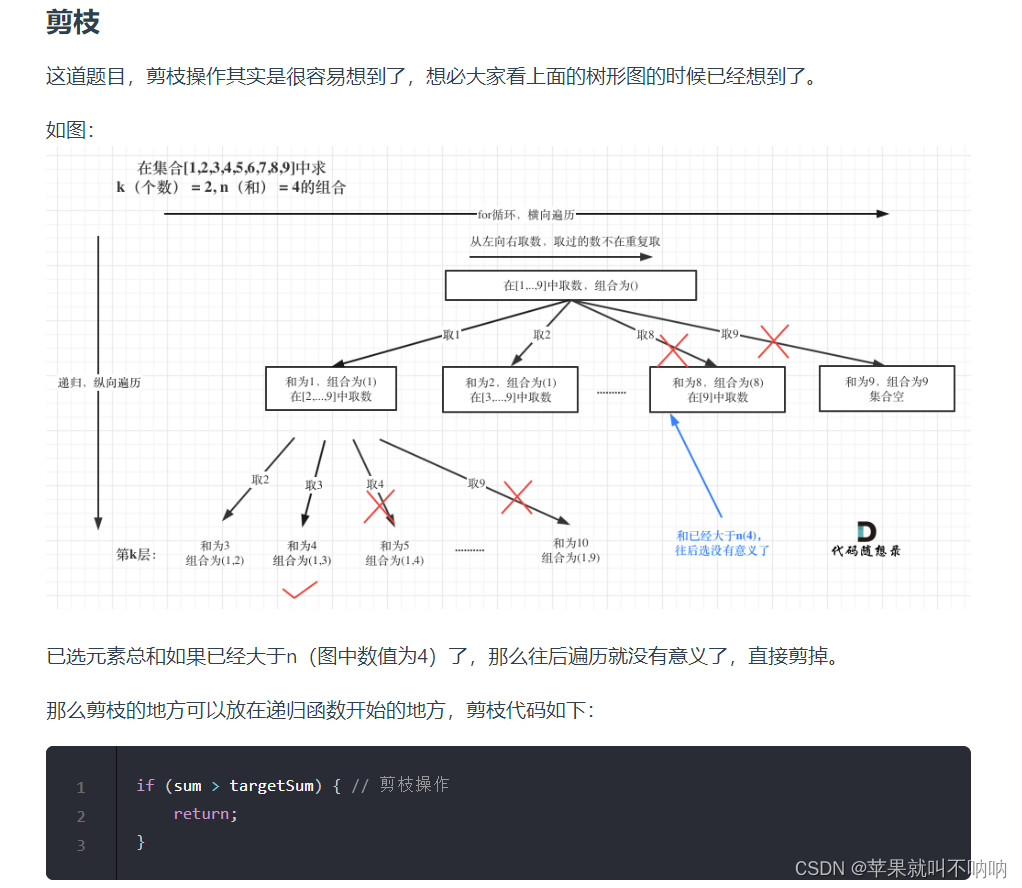
解法: 回溯+剪枝
class Solution {
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new ArrayList<>();
int sum = 0;
public List<List<Integer>> combinationSum3(int k, int n) {
backtracking(k,n,1);
return result;
}
public void backtracking(int k, int n, int startindex){
// 终止条件
if(sum >n) return; // 剪枝 如果sum已经大于n了,那就return
if(sum == n){
if(path.size() == k){
result.add(new ArrayList<>(path));
}
return;
}
for(int i = startindex; i <= 9; i++){
path.add(i);
sum += i;
backtracking(k,n,i+1);
sum -= i; // 回溯
path.removeLast(); //回溯
}
}
}