目录
前言
P114-P120
推荐系统
协同过滤
均值归一化
协同过滤的tensorflow实现
查找相关项目
P121-P130
基于内容的过滤
强化学习
P131-P142
状态动作值函数定义
Bellman方程
随机环境
连续状态空间应用实例
前言
这是吴恩达机器学习笔记的第七篇,第六篇笔记请见:
吴恩达机器学习全课程笔记第六篇
完整的课程链接如下:
吴恩达机器学习教程(bilibili)
推荐网站
scikit-learn中文社区
吴恩达机器学习资料(github)
P114-P120
推荐系统

如果在上述的基础上,我们还拥有每部电影的一些特征
对于第一个用户而言,可以根据下面的方式去计算一个得分去预估他会对某些电影的评分
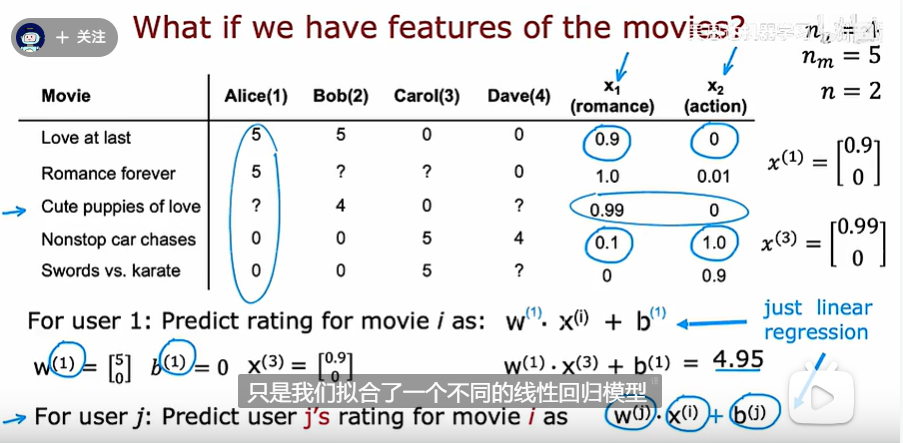
对于这个算法,我们接下来研究它的成本函数

通过最小化成本函数来学习、训练我们想要得到的参数

协同过滤
上述的预测是基于我们已知这些电影的某些特征的前提下,如果事先没有这些特征怎么办呢?

上面展示了如何根据参数去猜测某一部电影的特征
接下来我们根据成本函数去学习x1、x2的值,但需要注意的是:这里之所以有效是因为我们有四个用户的参数

把两种成本函数放在一起,变成协同过滤的成本函数表达式
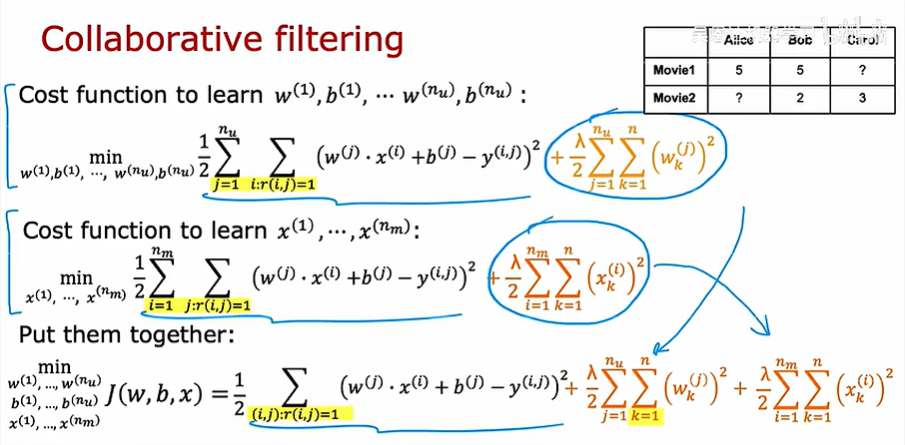
协同过滤的梯度下降:

下面将要把上述的算法从预测数字推广到预测二进制标签上去
下面是预测二进制标签在推荐系统中的一些应用实例

从回归到分类的转换和前面的类似,可以套入一个sigmoid函数

最后,预测标签的协同过滤的成本函数如下

均值归一化
增加归一化,将帮助算法对用户做出更好的预测
在正常情况下,对于一个还没有进行任何评价的用户,刚开始假定w、b全0,因为它并不会对最后的x做出影响,但是这样的话在训练之后w、b还会一直保持0,将无法得到有帮助的结果

进行均值归一化的过程如下所示

这种方法使得用户五与其它用户对五部电影的评分平均值相同,虽然直接给用户五赋值0有利于增加推荐算法的效率,但却不能使算法表现出很好的效果
同理,如果对列进行均值归一化,适用于一部电影还没被任何人评分的预测场景中
协同过滤的tensorflow实现
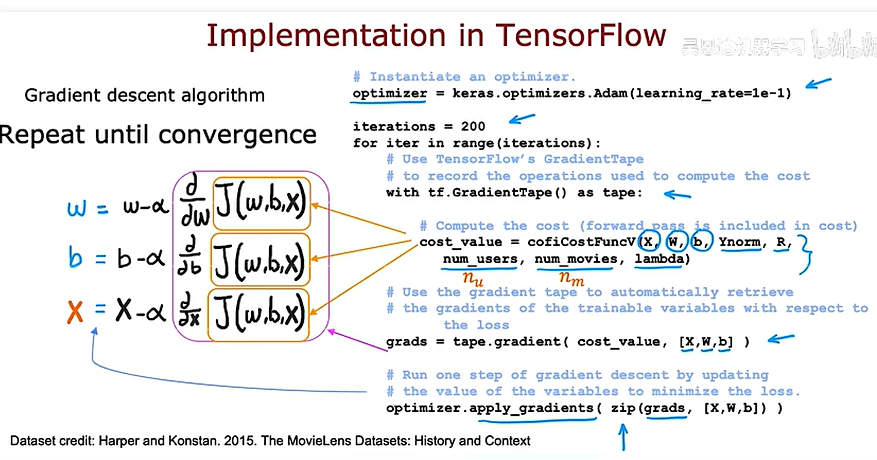
tensorflow的一个好处是可以为您计算出成本函数的导数是什么,所以你只需要实现成本函数,而不需要任何微积分的知识
下面是使用tensorflow进行梯度下降的一个例子

协同过滤的实现如下
查找相关项目
如果你去一个网上购物网站,正在看一个项目,网站可能会向你展示一些类似的东西

协同过滤的缺陷

P121-P130
基于内容的过滤
第二种推荐算法是基于内容的过滤,我们让它和协同过滤做出一个比较:

在协同过滤中,我们有许多用户给不同用户的打分,相比之下在基于内容的过滤中,我们有用户的特征和用户的特征,我们想要找到一种方法,在用户和项目之间找到良好的匹配,我们要做的就是计算一些向量,用户用vu,电影用vm,然后取他们点积,试图找到好的匹配,
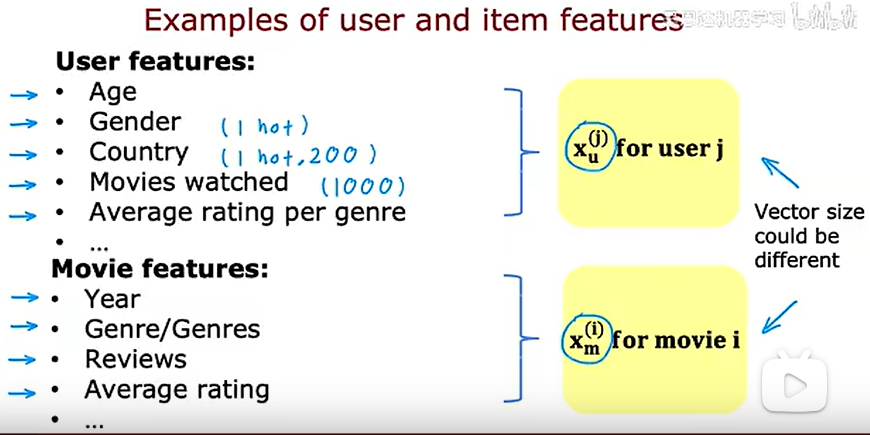
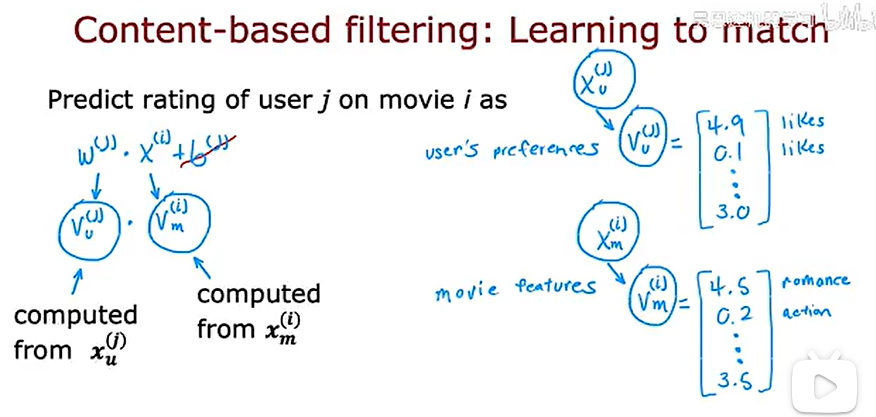
如何得到这两个向量,可以使用深度学习的方法
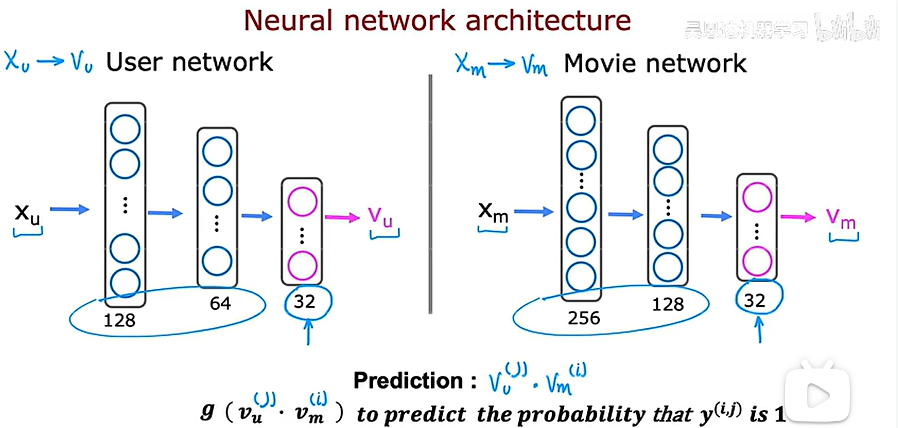
上述单独建立了两个神经网络,实际上可以把它画在一起
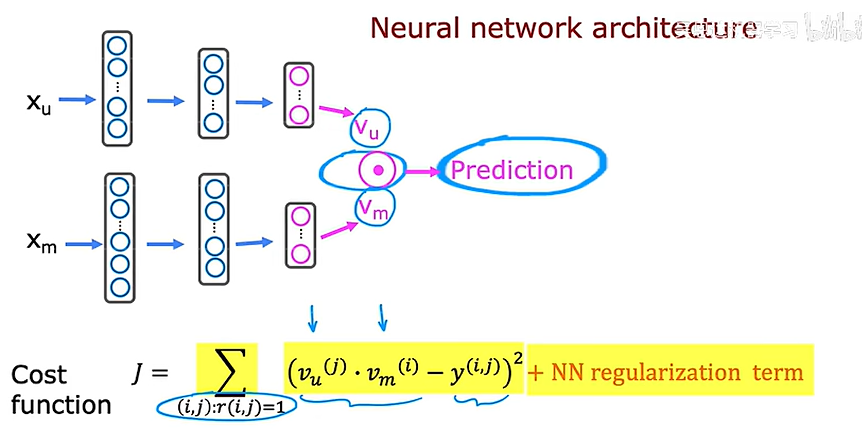
在得到上述的向量之后就可以找到相似的电影了

在大规模应用中,主要包含两个步骤:

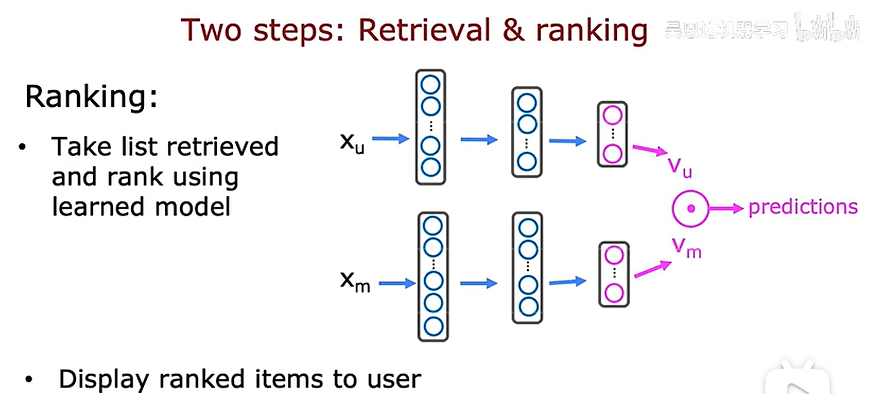
强化学习
强化学习(Reinforcement learning,RL)讨论的问题是一个智能体(agent) 怎么在一个复杂不确定的 环境(environment) 里面去极大化它能获得的奖励。通过感知所处环境的 状态(state) 对 动作(action) 的 反应(reward), 来指导更好的动作,从而获得最大的 收益(return),这被称为在交互中学习,这样的学习方法就被称作强化学习
以训练直升机自动驾驶为例,很难想监督学习那样得到x和理想作用y的数据集,这就是为什么很多控制机器人的任务重监督学习方法效果不好,强化学习的关键输入是一种叫做奖励的东西,它告诉直升机什么时候做得很好

下面是强化学习的一些应用

下面是火星探测器的一个简化例子,并标出了强化学习主要研究的四个指标

在这个例子中,让我们算一下向两边走的收益(return),其中γ是折现系数,是一个小于1的值
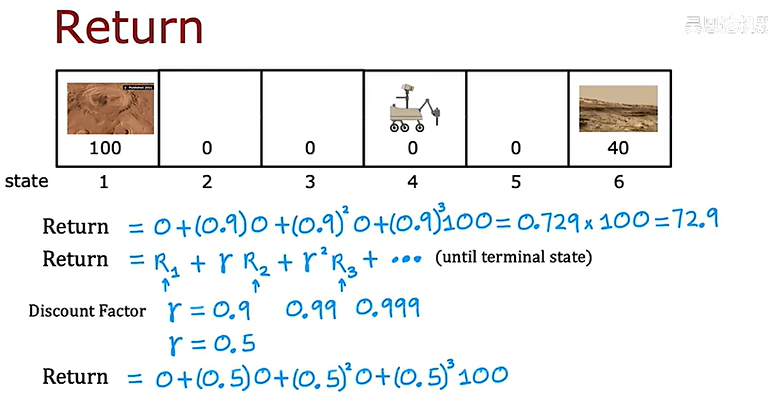

强化学习中决策和策略决定了接下来的要执行的动作

所以强化学习的目标就是找到这个策略(π)

下面对三个例子进行总结,回顾强化学习的概念

马尔科夫决策过程
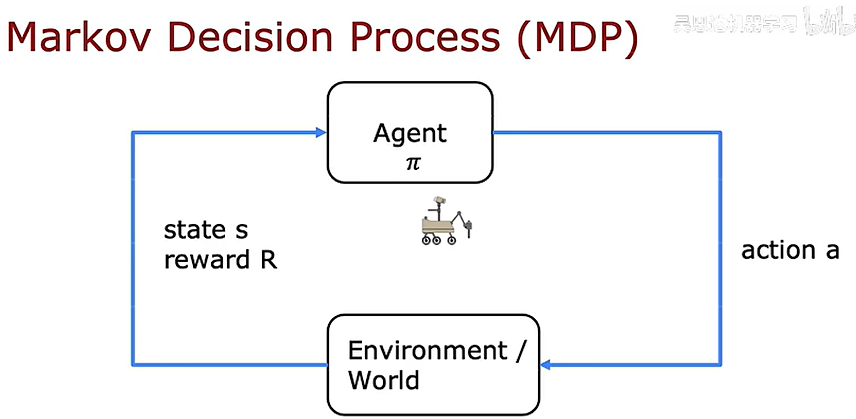
P131-P142
状态动作值函数定义
下面是强化学习中状态动作函数的定义和几个例子的计算,主要方框圈起来的是状态函数值返回值的条件,三个条件缺一不可

在进行行动决策的时候,只需要选出Q函数不同行动下的最大值对应的行动即可

Bellman方程
bellman方程可以帮助我们计算上述的状态动作值函数


随机环境
有时候命令火星探测器向左,但由于环境问题,无法向左
在随机化强化学习中,我们关注的不是最大回报,因为那是个随机数,我们感兴趣的是最大化所有可能的总奖励的平均值,这是后就引入了期望收益

由此可以更改上面学习的bellman方程为

连续状态空间应用实例

自动直升机的状态可以写成:

对于月球着陆器可以提供一些奖励供它进行强化学习

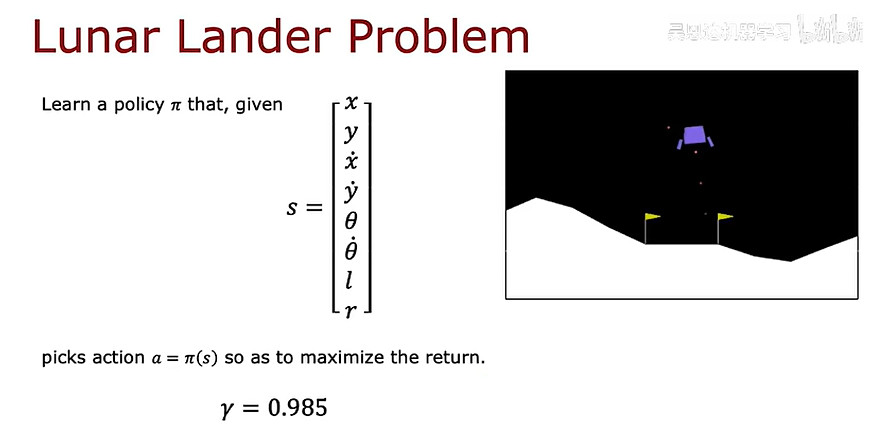
建立一个神经网络去学习状态动作函数

学习算法

强化学习的限制