文章目录
- 例题:到达目的地的方案数
- 题目描述
- 代码与解题思路
- 构建带权无向图的邻接矩阵
例题:到达目的地的方案数
题目链接:1976. 到达目的地的方案数
题目描述
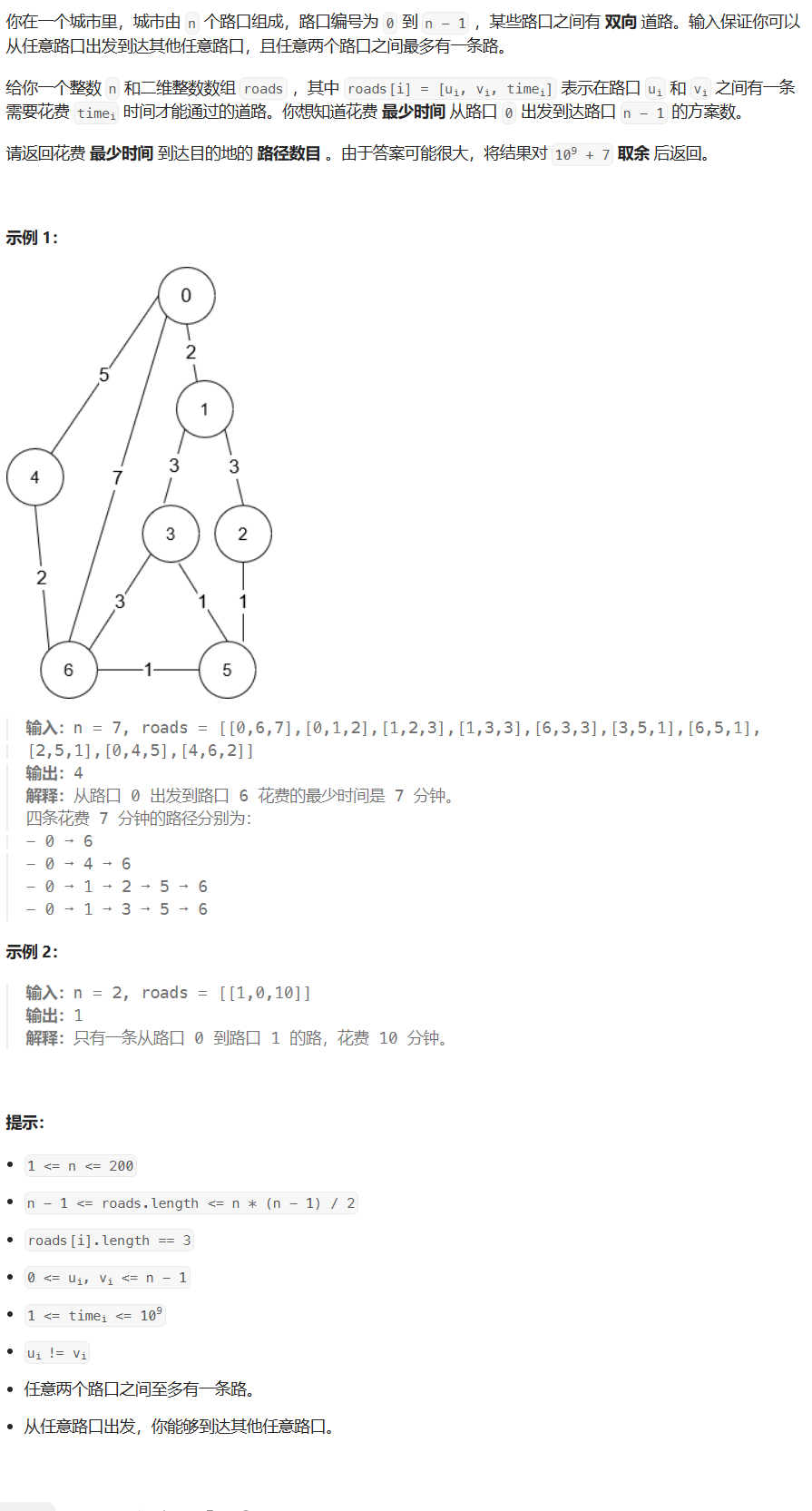
代码与解题思路
func countPaths(n int, roads [][]int) int {
g := make([][]int, n) // 构建邻接矩阵
for i, _ := range g {
g[i] = make([]int, n)
for j, _ := range g[i] {
g[i][j] = math.MaxInt / 2 // 到不了的地方就是无限大(初始化成这个值)
}
}
for _, v := range roads { // 无向图
x, y, d := v[0], v[1], v[2]
g[x][y] = d
g[y][x] = d
}
dis := make([]int, n) // dis 数组存储从起点到每个节点的当前已知最短距离
for i := 1; i < n; i++ {
dis[i] = math.MaxInt / 2
}
f := make([]int, n) // 存储到达每个节点的最短路径数
f[0] = 1 // 到自己是一条
done := make([]bool, n) // 标记每个节点是否被处理
for {
x := -1
for i, ok := range done {
// 找下一个未被处理的节点,x < 0 代表第一次进去
// 而 x 代表的是未被处理过的节点中,到起点距离最短的节点
if ok == false && (x < 0 || dis[i] < dis[x]) {
x = i
}
}
if x == n-1 { // 走到第 n-1 个节点了
return f[n-1]
}
done[x] = true // 这个节点被处理了
// 遍历从 x 出发能直接走到的所有下一个节点
// g[x] 的下标是 y, 存的值是 d
for y, d := range g[x] {
newDis := dis[x] + d // 遍历到到下一个节点的所有距离(当前距离+每条路的边权)
if newDis < dis[y] { // 找到了一条更短的路径
dis[y] = newDis // 更新 dis[y]
f[y] = f[x] // 下一个节点就是 y,让 f[y] 继承前面的路径数量
} else if newDis == dis[y] { // 又多了一条最短路径
f[y] = (f[y] + f[x]) % 1_000_000_007 // 路径的情况就多了 f[x] 种(可以画图理解)
}
}
}
}
构建带权无向图的邻接矩阵
g := make([][]int, n) // 构建邻接矩阵
for i, _ := range g {
g[i] = make([]int, n)
for j, _ := range g[i] {
g[i][j] = math.MaxInt / 2 // 到不了的地方就是无限大(初始化成这个值)
}
}
for _, v := range roads { // 无向图
x, y, d := v[0], v[1], v[2]
g[x][y] = d
g[y][x] = d
}