目录
- 看不见的手
- ljj的方块
- 零它来了
- 宝石转换
- ljj的距离
- 零它走了
- 彩蛋
题目
【A NKOJ-P8629】 看不见的手 40pts
考试思路:
这道题一看数据范围就知道是 O ( n ) O(n) O(n)的结论题,考试的时候脑子抽筋偏分输出1得了40pts;
正解:
他说呆呆会使总利润最高,那我们就从呆呆的角度去思考他的最优解;不难发现,呆呆赚取的利润是 卖出点价格 − 买入点价格 {\small\ \mathsf{卖出点价格}-\mathsf{买入点价格}} 卖出点价格−买入点价格;而在每个点呆呆可以买很多个口罩( T T T允许的话),所以呆呆肯定会在使数对 ( a i , a j ) (a_i,a_j) (ai,aj)的 a j − a i a_j-a_i aj−ai差值最大的 ( i , j ) (i,j) (i,j)点买入卖出;而我们要使呆呆少赚钱,我们只需要将这个数对变为: ( a i + 1 , a j ) 或 ( a i , a j − 1 ) (a_i+1,a_j){\small\ \mathsf{或}}(a_i,a_j-1) (ai+1,aj) 或(ai,aj−1),花费为1;
思路很明显了,由于使 a j − a i a_j-a_i aj−ai差值最大的 ( i , j ) (i,j) (i,j)可能不止一个,所以我们只需要求出这样的 ( i , j ) (i,j) (i,j)有多少个再乘上每一个数对的价值 1 1 1,就是答案
Ac Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,t,a[100005];
int minnum,maxnum,ans;
signed main(){
scanf("%lld%lld",&n,&t);
for(int i=1;i<=n;i++){scanf("%lld",&a[i]);}
minnum=a[1];
for(int i=2;i<=n;i++){
minnum=min(minnum,a[i-1]);
if(a[i]-minnum>maxnum){
maxnum=a[i]-minnum;
ans=0;
}
if(a[i]-minnum==maxnum){ans++;}
}
printf("%lld",ans);
return 0;
}
【B NKOJ-P10089】ljj的方块 15pts
考试思路:
输出0,直接骗分;(逃
正解:
先枚举其中任意两个有小黑子的点,在用公式推出剩余两个点的坐标,判断这两个点是否是在小黑子上,推理过程如图,其中涂色三角形是全等的,我们可以利用全等导边;(这个十分滴恶心)
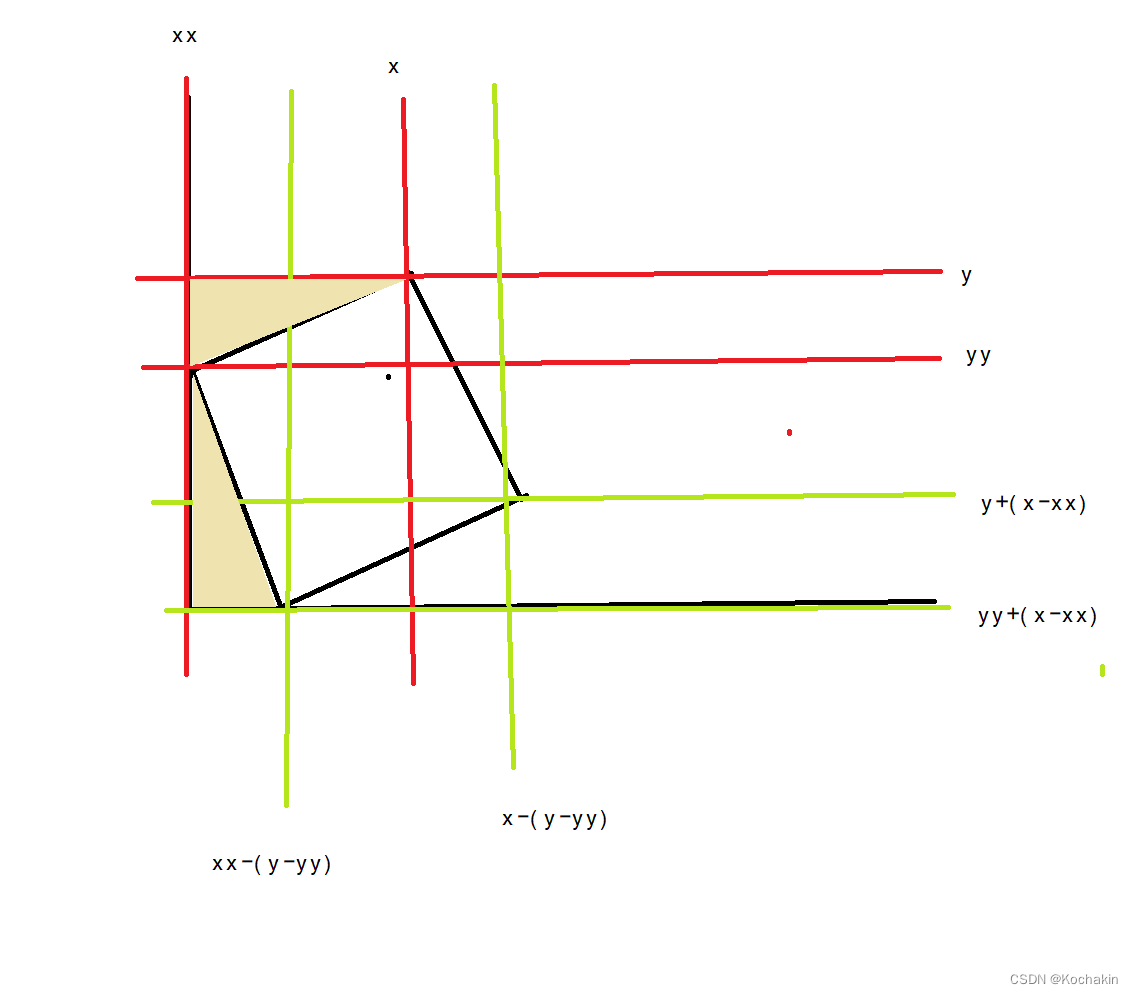
所以我们可以得到下面的结论
x
1
=
y
y
+
(
x
−
x
x
)
y
1
=
x
x
+
(
y
−
y
y
)
x
2
=
y
+
(
x
−
x
x
)
y
2
=
x
+
(
y
−
y
y
)
x1=yy+(x-xx) \\ y1=xx+(y-yy) \\ x2=y+(x-xx) \quad \\ y2=x+(y-yy)\quad
x1=yy+(x−xx)y1=xx+(y−yy)x2=y+(x−xx)y2=x+(y−yy)
最后一定要记得除2去去重!
Ac Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
char mapp[10][10];
int n,ans=0;
struct lyt{
int x,y;
}dis[100005];
signed main(){
for(int i=1;i<=9;i++){
for(int j=1;j<=9;j++){
cin>>mapp[i][j];
if(mapp[i][j]=='#'){
dis[++n].x=i;dis[n].y=j;
}
}
}
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
int x=dis[i].x,y=dis[i].y;
int xx=dis[j].x,yy=dis[j].y;
int x1=xx-(y-yy);
int y1=yy+(x-xx);
int x2=x-(y-yy);
int y2=y+(x-xx);
if(x1<0||x1>9||x2<0||x2>9||y1<0||y1>9||y2<0||y2>9){continue;}
if(mapp[x1][y1]=='#'&&mapp[x2][y2]=='#'){
printf("\nx,y:%lld %lld %lld %lld\n",x,y,xx,yy);
printf("xxyy:%lld %lld %lld %lld\n",x1,y1,x2,y2);
ans++;
}
}
}
printf("%lld",ans/2);
return 0;
}
【C NKOJ-P10086】零它来了 100pts
考试思路:
一道很水的模拟,但是要开点高科技 ,普通cin>>;cout>>:会T,我用了#pragma GCC optimize(2)+std::ios::sync_with_stdio(false); 双重优化卡过此题,这是本蒟蒻第一个Accepted的题;
Ac Code
#include<bits/stdc++.h>
#pragma GCC optimize(2)
#define int long long
using namespace std;
int t,n,num;
string s,p;
signed main(){
std::ios::sync_with_stdio(false);
cin>>t;
while(t--){
cin>>s;n=s.size();p=s;num=0;
if(s[0]=='0'||s[n-1]=='0'){cout<<s<<endl;continue;}
for(int i=0;i<n;i++){
if(s[i]=='0'&&s[i+1]=='0'){cout<<s<<endl;num=1;break;}
if(s[i]=='0'){p[i]='_';}
}
if(num){continue;}
else{cout<<p<<endl;}
}
return 0;
}
【D NKOJ-P10088】宝石转换 100pts
考试思路
递归解题,以下公式中的 a [ A − n ] a[A-n] a[A−n]表示 a a a颗 n n n级红宝石, b [ B − n ] b[B-n] b[B−n],表示 b b b颗 n n n级蓝宝石;
∵ a [ A − n ] ⟺ a [ A − ( n − 1 ) ] + a x [ B − n ] ∵ a x [ B − n ] ⟺ a x [ A − ( n − 1 ) ] + a x y [ B − ( n − 1 ) ] ∵ b [ B − n ] ⟺ b [ A − ( n − 1 ) ] + b y [ B − ( n − 1 ) ] \because a[A-n]\Longleftrightarrow a[A-(n-1)]+ax[B-n] \\\because ax[B-n]\Longleftrightarrow ax[A-(n-1)]+axy[B-(n-1)]\\\because b[B-n]\Longleftrightarrow b[A-(n-1)]+by[B-(n-1)] ∵a[A−n]⟺a[A−(n−1)]+ax[B−n]∵ax[B−n]⟺ax[A−(n−1)]+axy[B−(n−1)]∵b[B−n]⟺b[A−(n−1)]+by[B−(n−1)]
∴ a [ A − n ] + b [ B − n ] ⟺ ( a + a x + b ) [ A − ( n − 1 ) ] + ( a x y + b y ) [ B − ( n − 1 ) ] \therefore a[A-n]+b[B-n] \Longleftrightarrow (a+ax+b)[A-(n-1)]+(axy+by)[B-(n-1)] ∴a[A−n]+b[B−n]⟺(a+ax+b)[A−(n−1)]+(axy+by)[B−(n−1)]
以上即为推论:
Ac Code
#include<bits/stdc++.h>
#pragma GCC optimize(2)
#define int long long
using namespace std;
int n,x,y;
int dfs(int h,int l,int a,int b){//a,b为个数,h,l为等级,按照上述结论递推(各位dalao可以用效率更高的循环代替这个)
if(h<=1||l<=1){return b;}
return dfs(h-1,l-1,a*(x+1)+b,a*x*y+b*y);
}
signed main(){
scanf("%lld%lld%lld",&n,&x,&y);
printf("%lld",dfs(n,n,1,0));
return 0;
}
【E NKOJ-P10090】ljj的距离 70pts
考场思路
这题很明显,不能暴力枚举,但是我们可以发现通过求 s , t s,t s,t长度的lcm再取倍数就可以优化时间复杂度;即lcm优化(自己取的)
正解
首先,lcm优化的思路没有问题,我们可以把答案表示为,其中
d
d
d为公倍数区间中
s
,
t
s,t
s,t之间的距离:
s
l
o
n
g
×
n
l
c
m
(
s
l
o
n
g
,
t
l
o
n
g
)
×
d
\frac{s_{long} \times n}{\mathrm{lcm}(s_{long},t_{long})}\times d
lcm(slong,tlong)slong×n×d
我们发现,我们只能优化如何求出 d d d的值;不妨逆着思考—— d d d是 s i ≠ t i s_i \ne t_i si=ti的个数,很明显,我们求出 s i = t i s_i = t_i si=ti的个数更容易且可以·求出 t t t值,记其为 d 1 d_1 d1;
-
当一个 s i s_i si和 t j t_j tj在反转后正好可以重叠,那应当有:( x , y x,y x,y是反转多少次后他们重叠,是一个未知变量)
i + x × s l o n g = j + y × t l o n g i+x \times s_{long}=j+y \times t_{long} i+x×slong=j+y×tlong -
化简,即两边同时对 gcd ( s l o n g , t l o n g ) \gcd(s_{long},t_{long}) gcd(slong,tlong)取模,可得:
i ≡ j m o d gcd ( s l o n g , t l o n g ) i \equiv j \mod\gcd(s_{long},t_{long}) i≡jmodgcd(slong,tlong)
一下子思路就很清晰了:我们只需要用一个数组number[i][j]表示对在字符串
s
s
s当中
gcd
(
s
l
o
n
g
,
t
l
o
n
g
)
\gcd(s_{long},t_{long})
gcd(slong,tlong)取模值为
i
i
i的编号为
j
j
j的字母;接着遍历一遍
t
t
t,看一下哪些字母满足条件,遍历到一个把计数器加一,最后把计数器按照上述变形逆推回去,带入表达式中求解即可;
Ac Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,x,y;
int ans,gcds,lcms;
int number[1000005][30];
string sx,sy;
int get(char num){
return num-'a'+1;
}
int gcd(int a,int b){
return b?gcd(b,a%b):a;
}
signed main(){
scanf("%lld%lld",&n,&m);
cin>>sx>>sy;x=sx.size();y=sy.size();
gcds=gcd(max(x,y),min(x,y));lcms=x*y/gcds;
for(int i=0;i<x;i++){number[(i+1)%gcds][get(sx[i])]++;}
for(int i=0;i<y;i++){ans+=number[(i+1)%gcds][get(sy[i])];}
ans=(lcms-ans)*(n*x/lcms);
printf("%lld",ans);
return 0;
}
【F NKOJ-P10087】零它走了 44pts
考场思路
爆搜!记忆化爆搜!TLE爆搜!
很明显,4s的时限也救不了我的记忆化深搜;
正解
先给大家来一张图理解一下:
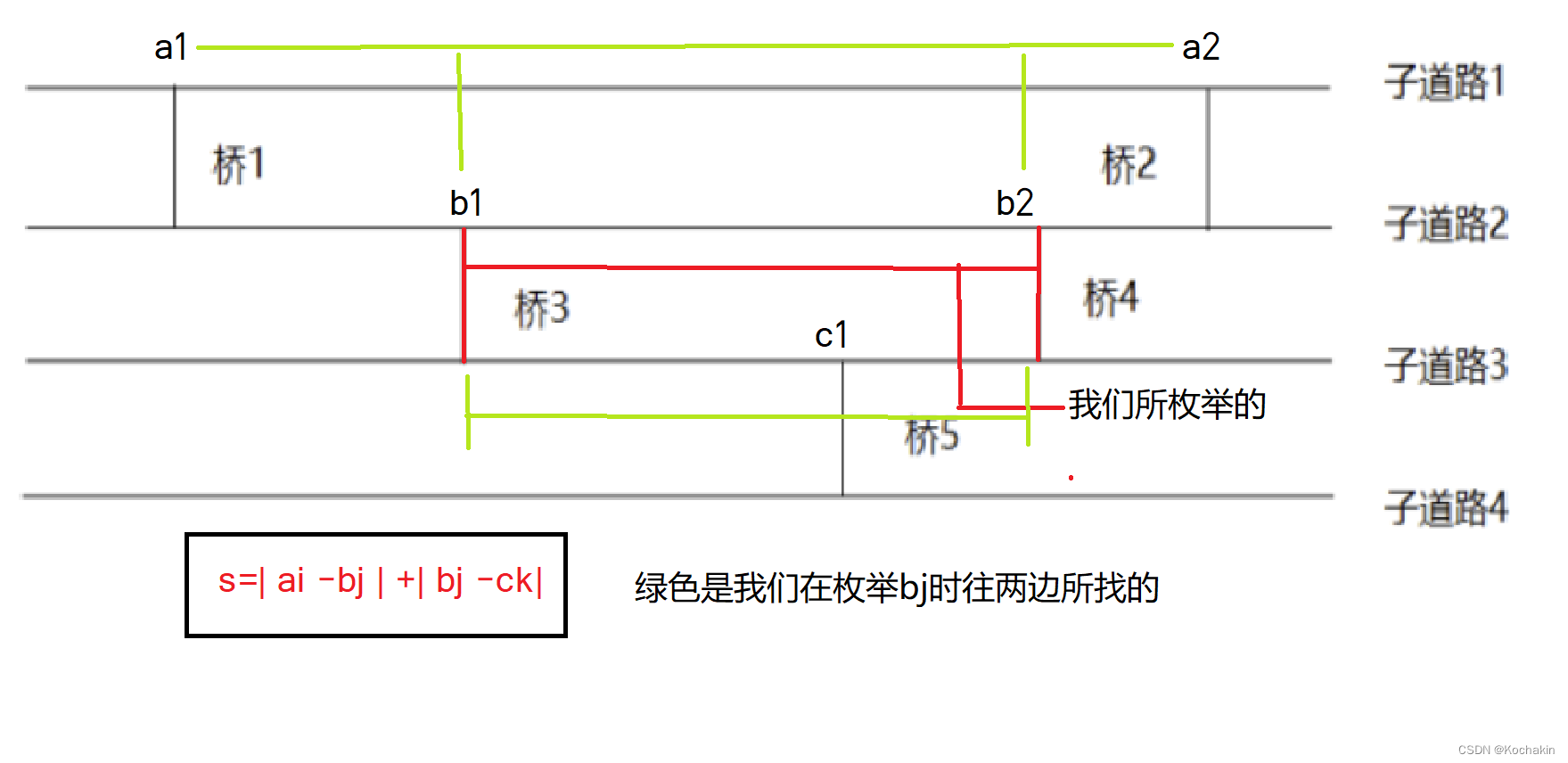
因为我们要求的是图中
s
s
s的最小值,所以我们一次枚举每一座“B桥”的情况;
- 对于第 i i i座“B桥”,是经过这座桥路径最短的“A桥”“C桥”的坐标一定是在所有“AC桥中”最靠近这座桥坐标的那一座,所以我们只需要选择对于当前B桥,应当选择左或是右边的“AC桥”即可;
- 对于选择“AC桥”也有优化,我们先对每一组桥的坐标进行排序,然后发现:当前B桥左边的最近桥肯定在上一座B桥最近桥的右边或是就是上一座B桥最近桥,于是我们只需要提前存储上一个最近桥的编号,从那里开始枚举,知道这个桥的坐标在当前“B桥”的左边或本身;
以上即为思路,实现的时候还是有很多细节,建议诸位自己画个图模拟一下样例;
Ac Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxnum=10000000000;
int t,a,b,c;
int da[100005],db[100005],dc[100005];
int mina,minb,minc,minnum;
int nexta,nextc;
signed main(){
scanf("%lld",&t);
while(t--){
scanf("%lld%lld%lld",&a,&b,&c);minnum=maxnum;nexta=nextc=1;
for(int i=1;i<=a;i++){scanf("%lld",&da[i]);}
for(int i=1;i<=b;i++){scanf("%lld",&db[i]);}
for(int i=1;i<=c;i++){scanf("%lld",&dc[i]);}
sort(da+1,da+a+1);sort(db+1,db+b+1);sort(dc+1,dc+c+1);
for(int i=1;i<=b;i++){
int time_min=maxnum,drta,drtc;
for(int j=nexta;j<=a;j++){
if(time_min>abs(db[i]-da[j])){time_min=abs(db[i]-da[j]);drta=j;}
if(da[j]>=db[i]||j==a){nexta=drta;break;}
}
time_min=maxnum;
for(int j=nextc;j<=c;j++){
if(time_min>abs(db[i]-dc[j])){time_min=abs(db[i]-dc[j]);drtc=j;}
if(dc[j]>=db[i]||j==c){nextc=drtc;break;}
}
int longs=abs(db[i]-da[drta])+abs(db[i]-dc[drtc]);
if(minnum>longs){minnum=longs;mina=drta;minb=i;minc=drtc;}
}
printf("%lld %lld %lld\n",da[mina],db[minb],dc[minc]);
}
return 0;
}
完结撒花-彩蛋
- ps:这场比赛让蒟蒻有了NK彩名
- ps:蒟蒻的第一篇游记,以后的游记都会归档在“其他特辑”当中,欢迎各位dalao批评
- ps:最近期末考试刚刚完,所以咕了这么久才发文