hi，代噶候。今天带大家认识一下二叉树，这个二叉树在我看来确实很有难度，但是不要怕，，鲁迅先生曾经说过，真正的勇士敢于面对惨淡的人生，敢于正视淋漓 的鲜血，下面让我们开始吧，先看看大纲
🚀1.什么是树
🚀2.树的相关概念
🚀3.什么是二叉树
🚀4.二叉树的相关概念
🚀5.二叉树的基本操作
什么是树呢？？？
树是一种非线性的结构，由n个结点组成，之所以叫做树，是因为它是根朝上，叶子朝下的结构，和现实中的树很像。
树的几个注意的点
1.一棵树只有一个根节点
2.树和链表不一样。没有所谓的前驱，只有左树和右树
3.树是递归实现的
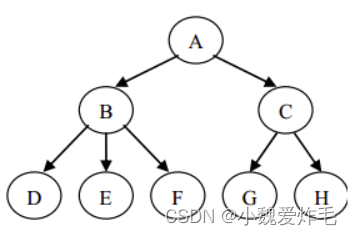
现在对树的相关概念进行介绍
1.结点的度：树的子树的个数 ，上图中A的度为2
2.树的度：所有节点数的最大值叫做树的度，上图中树的度为5
3.叶子结点：没有左子树并且没有右子树
4.双亲结点：若一个结点有孩子结点，那么该结点为双亲节点
5.孩子结点：双亲结点的孩子叫做孩子结点
6.根节点：没有父亲结点的结点；
7.树的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推
8.树的高度或深度：结点的最大层次
树要怎么表示呢
有双亲表示法
孩子表示法
孩子双亲表示法
孩子兄弟表示法
class Node {int value ; //树的存储的值Node fifirstChild ；//第一个孩子引用Node nextBrother ; //第二个孩子引用
这个了解即可
现在重头戏来了：二叉树来了
先了解一下二叉树的概念
就是每个结点的度不能超过2的树
画个图
这个图就是一个二叉树
满二叉树：
二叉树的每一个结点都有左子树和右子树
如图
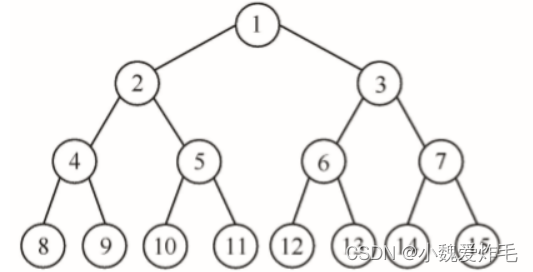
完全二叉树
不一定满。但是在进行层次遍历的时候顺序一定是相连的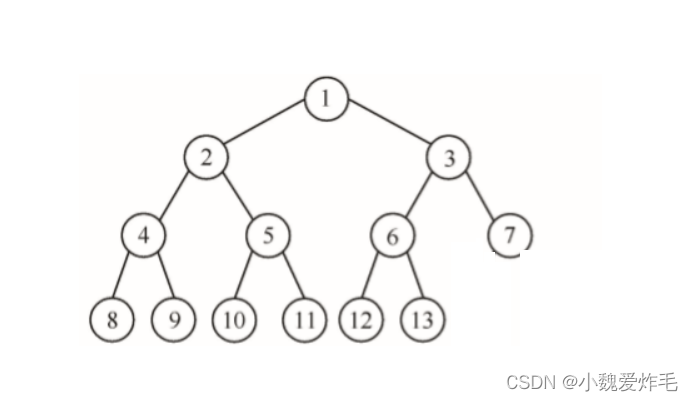
在进行层次遍历的时候有1,2,3,4,5,6,7,8,9,10,11,12,13
这就是有序的
什么是无序的呢，再画个图
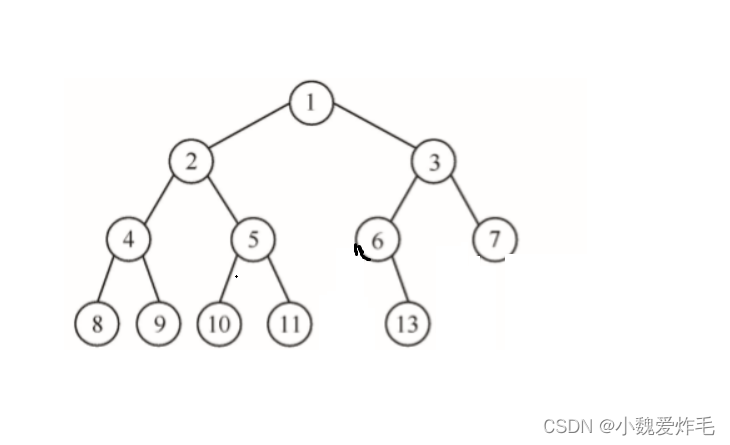
这就不是一个完全二叉树，不连续，11和13之间差一个12
由此可看，满二叉树是一种特殊的完全二叉树
二叉树的性质
若规定
根结点的层数为
1
，则一棵
非空二叉树的第
i层有2^（i-1）
(i>0)
个结点
若规定只有
根结点的二叉树的深度为
1
，则
深度为
K
的二叉树的最大结点数是2^k-1
(k>=0)
对任何一棵二叉树
,
如果其
叶结点个数为
n0,
度为
2
的非叶结点个数为
n2,
则有
n0
＝
n2
＋
1
总结点数n=n0+n1+n2;
对于具有
n
个结点的完全二叉树
，如果按照
从上至下从左至右的顺序对所有节点从
0
开始编号
，则对于
序号为
i
的结点有
：
若
i>0
，
双亲序号：
(i-1)/2
；
i=0
，
i
为根结点编号
，无双亲结点
若
2i+1<n
，左孩子序号：
2i+1
，否则无左孩子
若
2i+2<n
，右孩子序号：2i+2, 否则无右孩子
具有
n
个结点的完全二叉树的深度
k
为log(n+1)向
上取整
有一个关于完全二叉树的点
当有n个结点，n 为偶数个结点时，度为1的结点的个数为1，n为奇数结点的时候，度为1的结点的个数为0
二叉树的存储
二叉树的存储分为链式存储额和顺序存储
今天先讲链式存储
//孩子表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
}下面来说一说二叉树的遍历方式
1.前序遍历 根左右
2.中序遍历 左根右
3.后序遍历 左右根
4.层次遍历 从左至右
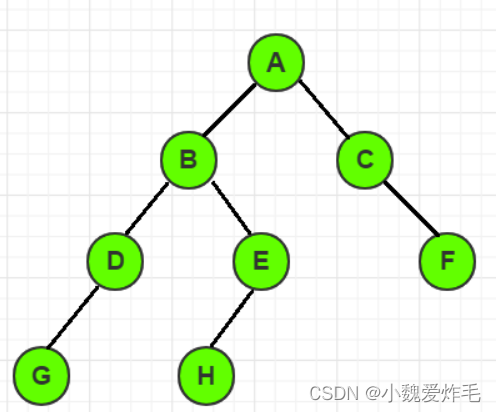
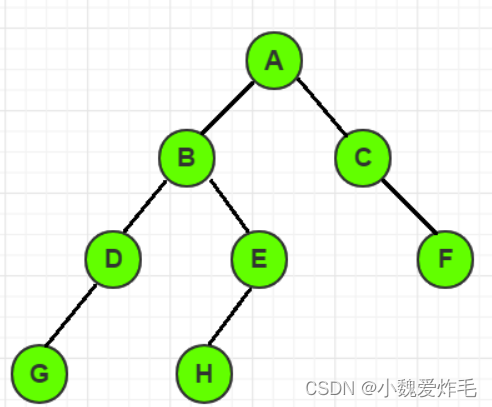
就拿这棵树来举例
前序遍历：ABDGEHCF
中序遍历：GDBHEACF
后序遍历：GDHEBFCA
层次遍历：ABCDEFGH
还有一种考法，多出现在选择题里面，已知前序和中序，求后序。或者已知中序和后序，求前序
下面是二叉树的基本操作
public class BinaryTree {
static class TreeNode {
public char val;
public TreeNode left;//左孩子的引用
public TreeNode right;//右孩子的引用
public TreeNode(char val) {
this.val = val;
}
}
public TreeNode root;
/**
* 创建一棵二叉树 返回这棵树的根节点
*
* @return
*/
public TreeNode createTree() {
TreeNode A=new TreeNode('A');
TreeNode B=new TreeNode('B');
TreeNode C=new TreeNode('C');
TreeNode D=new TreeNode('D');
TreeNode E=new TreeNode('E');
TreeNode F=new TreeNode('F');
TreeNode G=new TreeNode('G');
TreeNode H=new TreeNode('H');
A.left=B;
B.left=D;
B.right=E;
C.left=F;
C.right=G;
E.right=H;
this.root=A;
return root;
}
// 前序遍历
public void preOrder(TreeNode root) {
if(root==null){
return;
}
System.out.println(root.val+"");
preOrder(root.left);
preOrder(root.right);
}
// 中序遍历
void inOrder(TreeNode root) {
if(root==null){
return;
}
inOrder(root.left);
System.out.println(root.val+"");
inOrder(root.right);
}
// 后序遍历
void postOrder(TreeNode root) {
if(root==null){
return;
}
postOrder(root.left);
System.out.println(root.val+"");
postOrder(root.right);
}
public static int nodeSize;
/**
* 获取树中节点的个数：遍历思路
*/
public int NodeSize;//成员变量
void size(TreeNode root) {
if(root==null){
return;
}
NodeSize++;
size(root.left);
size(root.right);
}
/**
* 获取节点的个数：子问题的思路
*
* @param root
* @return
*/
int size2(TreeNode root) {
if(root==null){
return -1;
}
int leftSize=size2(root.left);
int rightSize=size2(root.right);
return leftSize+rightSize+1;
}
/*
获取叶子节点的个数：遍历思路
*/
public static int leafSize = 0;//静态成员变量
void getLeafNodeCount1(TreeNode root) {
if(root==null){
return;
}
if(root.left==null&&root.right==null){
leafSize++;
}
getLeafNodeCount1(root.left);
getLeafNodeCount1(root.right);
}
/*
获取叶子节点的个数：子问题
*/
int getLeafNodeCount2(TreeNode root) {
if(root==null){
return -1;
}
if(root.left==null&&root.right==null){
return 1;
}
int leftSize=getLeafNodeCount2(root.left);
int rightSize=getLeafNodeCount2(root.right);
return leftSize+rightSize;
}
/*
获取第K层节点的个数
*/
int getKLevelNodeCount(TreeNode root, int k) {
if(root==null){
return -1;
}
if(k==1){
return 1;
}
int leftSize= getKLevelNodeCount(root.left,k-1);
int rightSize= getKLevelNodeCount(root.right,k-1);
return leftSize+rightSize;
}
/*
获取二叉树的高度
时间复杂度：O(N)
*/
int getHeight(TreeNode root) {
if(root==null){
return -1;
}
int leftHeight=getHeight(root.left);
int rightHeight=getHeight(root.right);
return (leftHeight>rightHeight)?leftHeight+1:rightHeight+1;
}
// 检测值为value的元素是否存在
TreeNode find(TreeNode root, char val) {
if(root==null){
return null;
}
if(root.val==val){
return root;
}
TreeNode leftNode= find(root.left,val);
if( leftNode!=null){
return leftNode;
}
TreeNode rightNode=find(root.right,val);
if(rightNode!=null){
return rightNode;
}
return null;
}
今天的分享先到这里，下期再见！！！
