Octopus: Comprehensive and Elastic User Representation for the Generation of Recommendation Candidates

背景：

多兴趣通道(channel)结构的多兴趣召回模型在兴趣通道数量上面存在两个问题

1. 兴趣通道较少，不能充分学习到用户的多个兴趣。
2. 兴趣通道较多，很多兴趣通道可能和用户兴趣不相关，这样会引入很多不相关的候选集，带来噪声；固定的 topK 策略会导致有噪声的兴趣也会召回到对应的候选集，从而挤占整体相关兴趣的候选数量，造成整体相关候选集数量下降；而且线上耗时和兴趣通道数据是线性相关，兴趣通道越多造成的耗时越大。

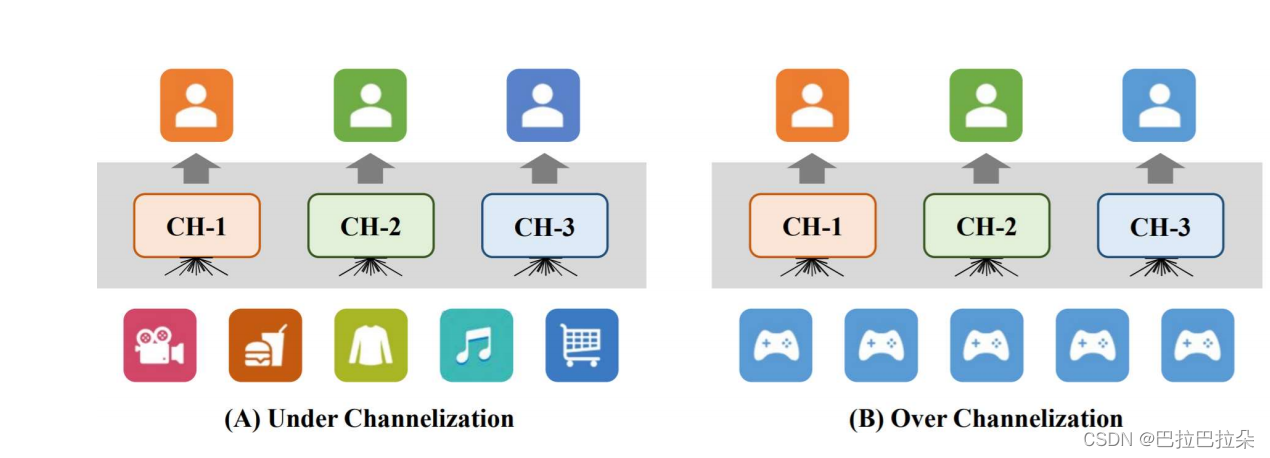
其实说的更简单点，2 个问题：就是多兴趣召回里面，不同用户产出的多个兴趣数量是固定的，没有个性化；每个兴趣向量召回的 topK 个候选，没有考虑不同兴趣的重要度

即如何实现个性化的兴趣数量、如何实现根据兴趣重要度去个性化选择候选数量。

解决方案：

预设多个兴趣通道，但是根据用户历史行为来激活部分兴趣通道，对激活的兴趣通道计算用户的兴趣向量。同时根据兴趣重要度来决定每个兴趣拉取候选集的 quota。

方案详情：

整体结构图如下：

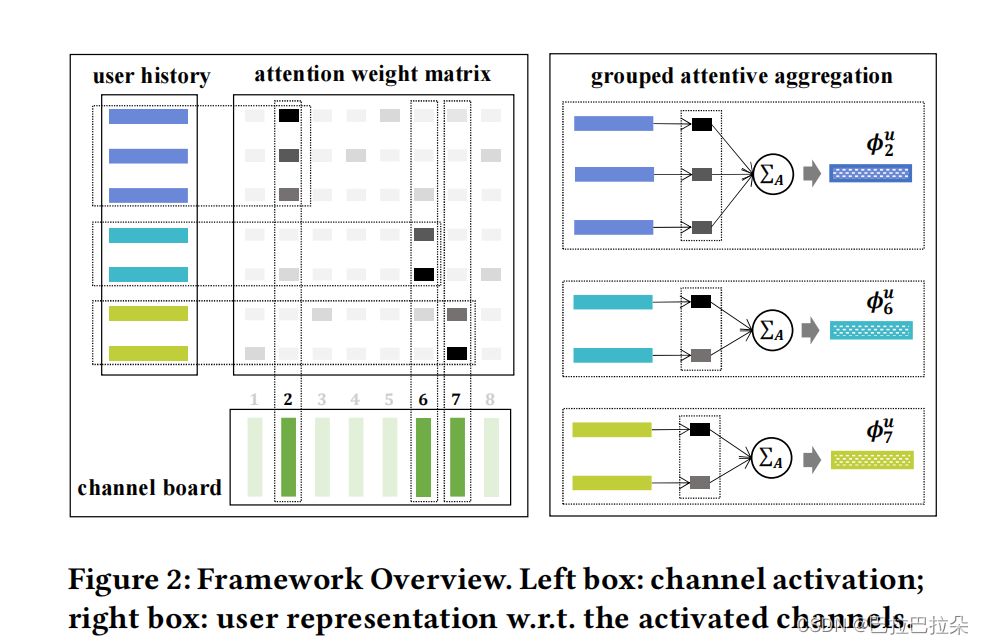
以上面的结果图为例，预设 M(图中M=8) 个全局的相互正交的兴趣通道，设兴趣向量的维度为 d，

解决第一个问题：如何实现不同用户的兴趣数量个性化

兴趣通道正交

怎么保证各个兴趣向量之间的正交性呢，即怎么保障 M 个兴趣通道对应的兴趣向量矩阵$\mathbf{H}\in R^{M\times d}$为正交矩阵，可以通过迭代的方式来，用户行为序列矩阵为$\mathbf{\Theta }\in R^{N\times d}$，
通过求兴趣向量矩阵正交基得到
$$argmin\sum _{\Theta }||\theta -\theta {\mathbf{H}}^T\mathbf{H}|{|}_2$$
另外通过正则项约束来进一步保证兴趣通道向量矩阵的正交性，其中$\mathbf{I}\in R^{M\times M}$是单位矩阵
$$||\mathbf{H}{\mathbf{H}}^T-\mathbf{I}|{|}_2$$

兴趣激活

假设用户序列长度为 N，首先将每个序列都投影到 M 个兴趣通道上面，即计算每个序列在 M 个兴趣通道上面的注意力分数（论文中用的是点乘），分数最大的兴趣通道作为激活的兴趣通道，用户 N 个序列就会得到 N 个注意力分数最大的通道，当然只有 M 个通道。以上图为例（M=8，N=7），有 3 个序列在兴趣通道 2 上面计算得到的注意力分数最大，有 2 个序列在兴趣通道 6 上面注意力分数最大，剩下还有 2 个序列在兴趣通道 7 上面注意力分数最大， 这 N=7 个序列行为总共激活了 3 个（兴趣通道 2、6、7）兴趣通道，那么这个用户最后产出的多兴趣数目为 3。这样就把最相关的一些兴趣通道给激活出来了，相关性弱的兴趣通道不会参与候选集召回。

兴趣聚合

上图中，序列行为 1、2、3 激活了兴趣通道 2，序列行为 3、4 激活了兴趣通道 6，序列行为 5、6 激活了兴趣通道 7。最终的用户兴趣向量通过 attention 的方式计算得到。第$l$个兴趣向量$h_l\in \mathbf{H}$由激活第$l$个兴趣通道的序列行为集合根据新计算的注意力分数得到，计算方式如下

$${\varphi }_l=\sum _{x_i\in \mathbf{X}}{a}_{i,l}{\theta }_{x_i}$$

$$a_{i,l}=\frac{\exp sim({\theta }_{x_i},h_l)}{{\sum }_{x_j\in \mathbf{X}}\exp sim({\theta }_{x_j},h_l)}$$
比如，第一个激活的兴趣通道 2，产出的用户兴趣向量是序列 1、2、3 在兴趣通道 2 上面的注意力权重，然后根据权重乘以行为向量，聚合得到第一个兴趣向量。

训练目标，本来是用户向量尽可能的学的好，即和 target物料向量在向量空间尽可能的接近，向量空间反应了相关性，向量空间距离最接近表示相关性最高，但是多个兴趣向量就不是这样了，因为用户兴趣是多样的，我们只需要选出 target 物料向量和兴趣向量距离最小的那个兴趣向量，然后最小化这个兴趣向量和 target 物料向量的距离，至于其他用户兴趣向量，不用 care。

解决第二个问题：如果实现不同兴趣对应的候选集数量个性化

2 种解决办法

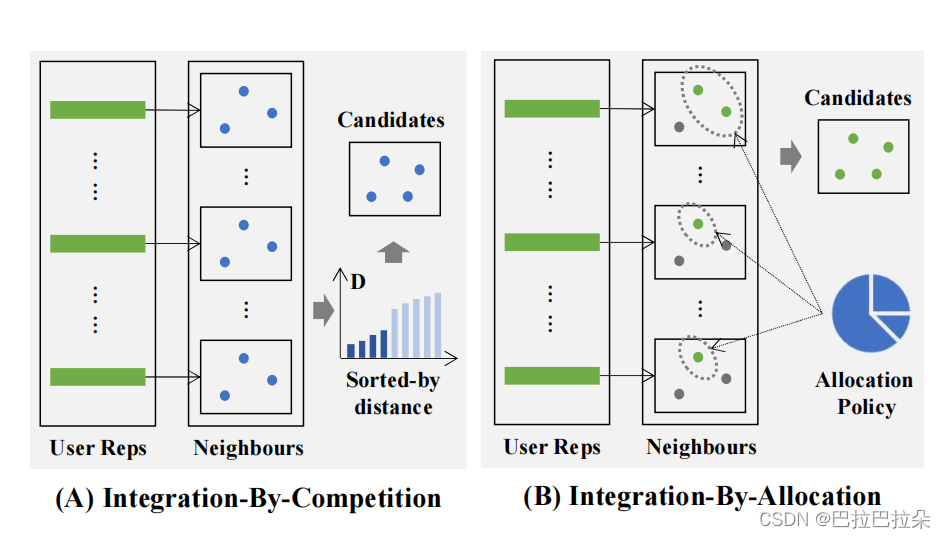
第一个：竞争式（Competition）

M 个兴趣向量，每个用户兴趣向量先各自召回 J 个候选，计算用户兴趣向量和各自候选集的距离，会得到 M*J 个距离，然后选择 topK 个距离最小的候选。不过有个问题，不同兴趣和候选集的距离可能不可比，比如某个兴趣，和它对应的候选距离天然都要小些，那么这个兴趣对应的候选最终会全部进入 topK 集合中，其他的兴趣可能因为距离天然要大些，可能一个也不会进入到最终的 topK 候选中。

第二个：分配式（Allocation）

从效率考虑，用一个 MLP 来建模兴趣重要度。将前面产出的多个兴趣向量作为模型输入，每个兴趣向量经过 MLP（$d\times d$和$d\times 1$后经过 sigmoid 激活），计算每个用户兴趣向量的相对重要性

$${\gamma }_i=\frac{MLP({\varphi }_i)}{\sum MLP({\varphi }_j)}$$

然后找到和 target 物料向量和距离最小的兴趣向量${\varphi }_k$，设置 label 为 1，计算${\gamma }_k$和 1 之间的交叉熵loss

兴趣重要度模型训练好之后，输入用户的多个兴趣向量，可以得到每个兴趣向量经过网络之后的兴趣重要度得分${\gamma }_i$，根据重要度来决定候选 quota 数量的分配，第$l$个兴趣向量对应的比例，计算如下

$${\beta }_l=\frac{({\gamma }_l{)}^{\alpha }}{\sum ({\gamma }_j{)}^{\alpha }}$$

其中$\alpha$是超参数

实验

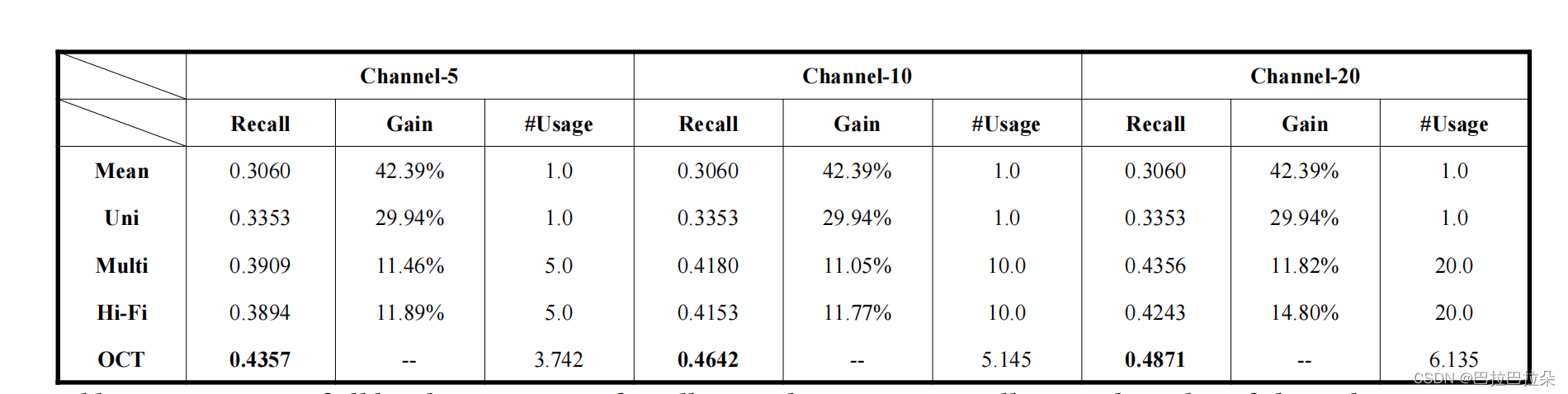
不同通道数量的比较

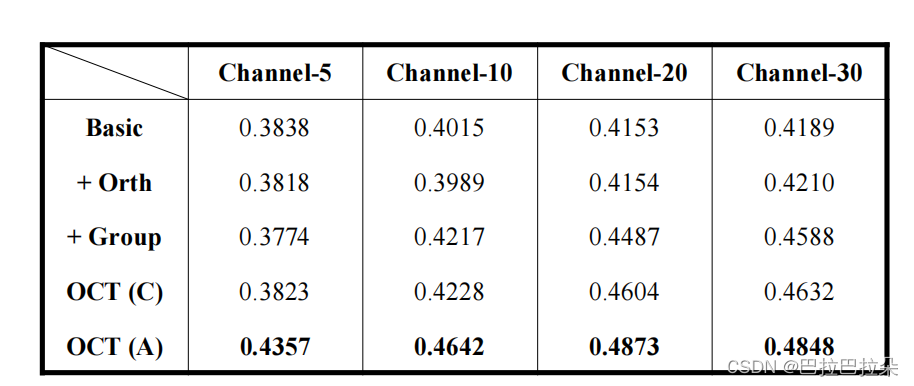
消融实验

+Orth 表示加兴趣通道正则化
+Group 表示加兴趣激活
OCT© 竞争式
OCT(A) 分配式