树的遍历
- 1.题目
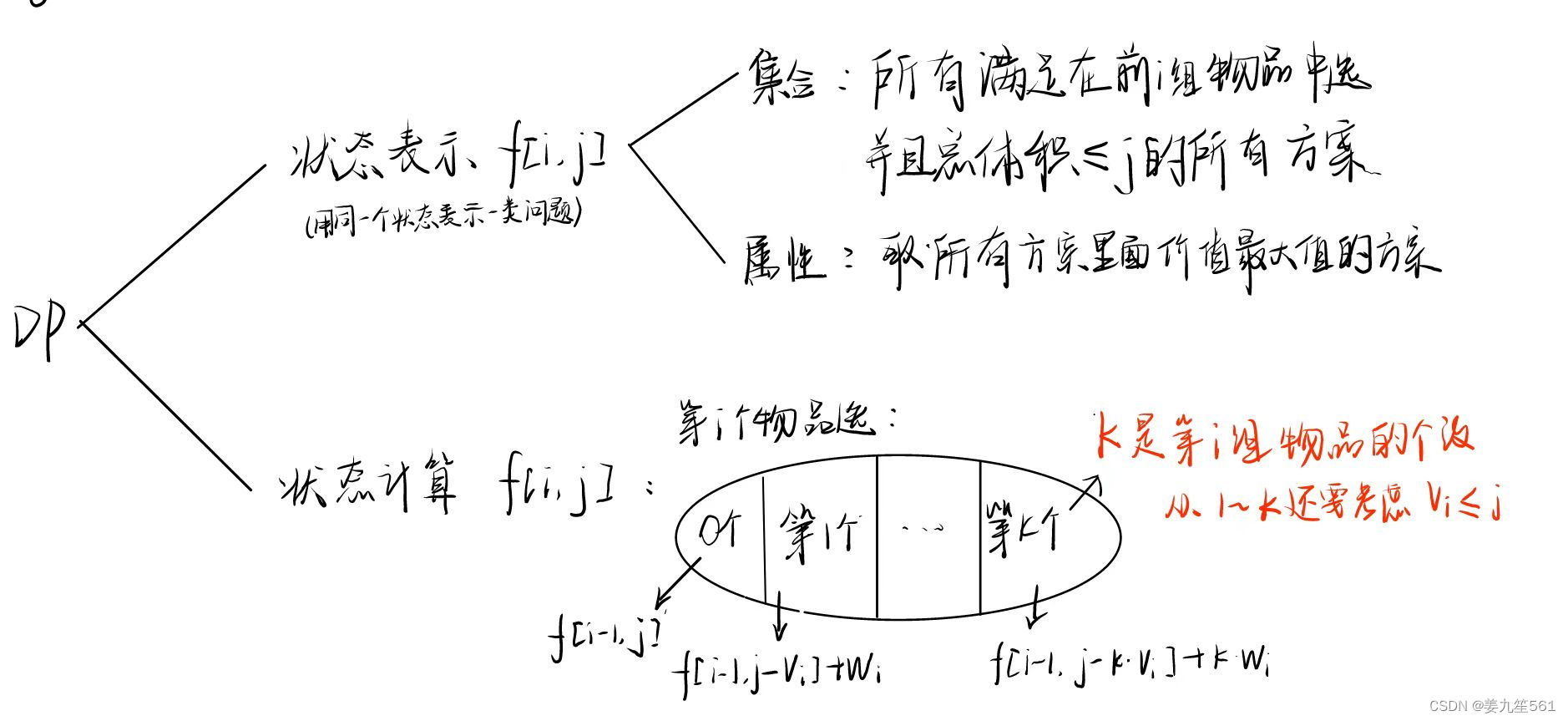
- 2.基本思想
- 3.代码实现
1.题目
一个二叉树,树中每个节点的权值互不相同。
现在给出它的后序遍历和中序遍历,请你输出它的层序遍历。
输入格式
第一行包含整数 N,表示二叉树的节点数。
第二行包含 N个整数,表示二叉树的后序遍历。
第三行包含 N 个整数,表示二叉树的中序遍历。
输出格式
输出一行 N
个整数,表示二叉树的层序遍历。
数据范围
1≤N≤30,
官方并未给出各节点权值的取值范围,为方便起见,在本网站范围为 1∼N。
输入样例1:
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
输出样例1:
4 1 6 3 5 7 2
2.基本思想
思路:
-
先根据后序和中序遍历结果构造二叉树
-
按层次遍历构造出来的二叉树
第一步:构造二叉树
-
存储结构使用两个哈希表:leftChile, rightChile。leftChile[i] = j: i 的左儿子是j,rightChilet同理
-
后序遍历的最后一个节点是跟节点,得到根节点后,递归构造根节点的左儿子和右儿子。
-
返回二叉树的根节点
-
也可以选择其他方式构造二叉树。
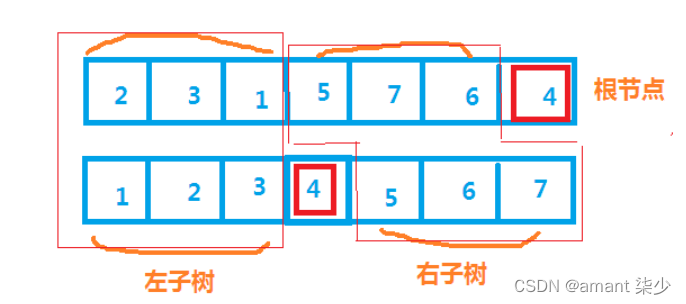
第二步:遍历二叉树
按层次遍历二叉树,使用bfs
-
根节点入队列。
-
当队列非空,队头的左右儿子入队列,队头出队。
3.代码实现
import java.util.*;
public class Main {
static int N = 40;
static int[] postorder = new int[N], inorder = new int[N];//后序 中序
static HashMap<Integer, Integer> pos = new HashMap<>();
static HashMap<Integer, Integer> l = new HashMap<>();// l<根节点的值,左子树根节点的值>
static HashMap<Integer, Integer> r = new HashMap<>();// r<根节点的值,右子树根节点的值>
private static int build(int il, int ir, int pl, int pr) {//中序 左右 后续 左右
int root = postorder[pr];//根节点 一定是 后序遍历 最后一个
int k = pos.get(root);// 获取根节点在中序遍历的下标
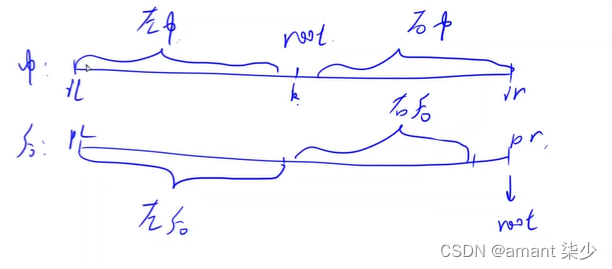
if (il < k) {// 根 k 有左子树
//il ~ k-1 是 左子树的所有节点,长度为 len = (k-1-il)
// pl ~ pl+len: 是后序遍历序列里边左子树的范围
int lroot = build(il, k - 1, pl, pl + k - 1 - il);
l.put(root, lroot);
}
if (ir > k) {// 根 k 有右子树
int rroot = build(k + 1, ir, pl + k - 1 - il + 1, pr - 1);
r.put(root, rroot);// root 的右子树的根节点是 rroot
}
return root;
}
private static void bfs(int root) {
Queue<Integer> q = new LinkedList();
q.add(root);
while (!q.isEmpty()) {
int t = q.poll();
System.out.print(t + " ");
// 如果此节点有左子树,入队
if (l.containsKey(t)) q.add(l.get(t));
// 如果此节点有右子树,入队
if (r.containsKey(t)) q.add(r.get(t));
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
for (int i = 0; i < n; i++) postorder[i] = sc.nextInt();//读入 后序遍历数组
for (int i = 0; i < n; i++) {//读入中序遍历
inorder[i] = sc.nextInt();
pos.put(inorder[i], i);// 记录中序遍历每个点的下标
}
int root = build(0, n - 1, 0, n - 1);//中序 后续
bfs(root);
}
}