【数据结构】一步一步实现AVL树

news2024/9/24 5:32:15

树和节点的定义

template<class K,class V>
class AVLTreeNode
{
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	pair<K, V> _kv;
	int _bf;

	AVLTreeNode(const pair<K,V>& kv)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_kv(kv)
		,_bf(0)
	{}
};

插入

bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(kv);
		if (kv.first > parent->_kv.first)
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}
		//父链接子，子要反向链接父
		cur->_parent = parent;

		//update bf
		while (parent)
		{
			if (cur == parent->_right)
			{
				parent->_bf++;
			}
			else
			{
				parent->_bf--;
			}

			if (parent->_bf == 1 || parent->_bf == -1)
			{
				parent = parent->_parent;
				cur = cur->_parent;
			}
			else if (parent->_bf == 0)
			{
				break;
			}
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				//rotate

			}
			else
			{
				assert(false);
			}
		}

		return true;
	}

平衡因子的调整

1.parent->bf等于1||-1,说明parent所在的子树高度变了，（因为插入前parent->bf等于0，插入前左右子树高度相等，现在有一边高了）需要继续向上更新平衡因子。
2.parent->bf等于2||-2，parent所在的子树不平衡，需要旋转处理这棵子树。
3.parent->bf等于0，parent所在的子树平衡无需更新。

旋转

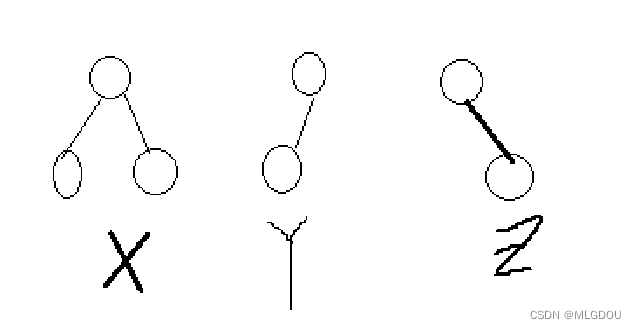
在这里插入图片描述
我们先定义有以上三种子节点，分别记为x，y，z，以便后文讲解。

左单旋

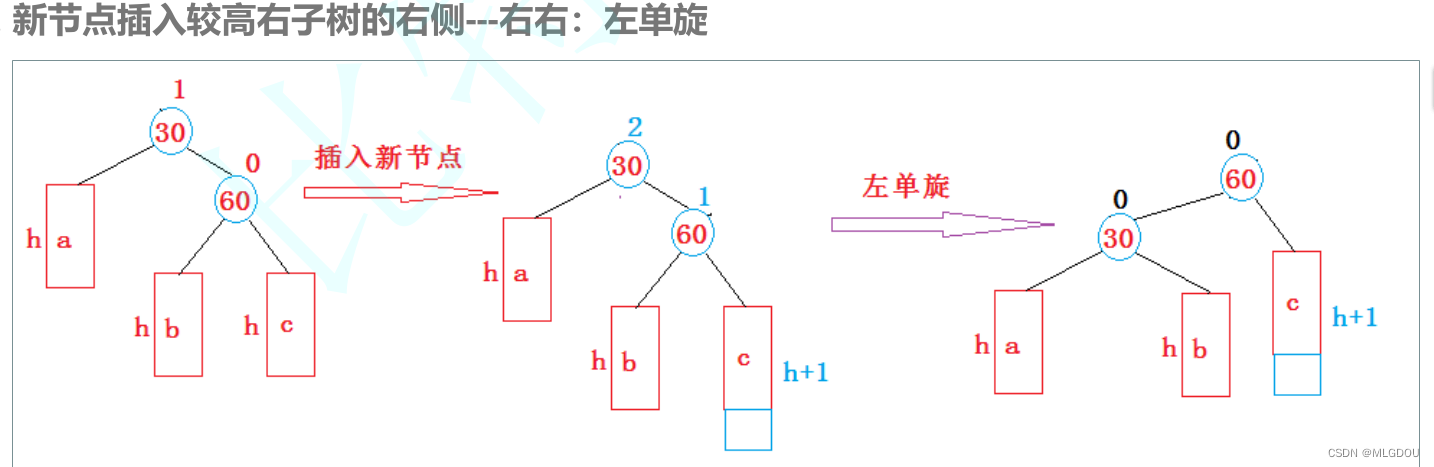
在这里插入图片描述
上述这种情况，c只能是x，若非那么c节点本身就要先旋转调整。
b变成了30的右边，30变成60的左边，60变成整棵树的根。
注意点：1.双向连接2.subRL可能为空3.parent是否为根
代码实现：

void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if(subRL)			
			subRL->_parent = parent;

		Node* ppNode = parent->_parent;

		subR->_left = parent;
		parent->_parent = subR;

		//判断上面是否有根
		if (ppNode == nullptr)
		{
			_root = subR;
			_root->_parent = nullptr;
		}
		else
		{
			if (ppNode->_left == parent)
			{
				ppNode->_left = subR;
				subR->_parent = ppNode;
			}
			else
			{
				ppNode->_right = subR;
				subR->_parent = ppNode;
			}
		}

		parent->_bf = subR->_bf = 0;
	}

右单旋

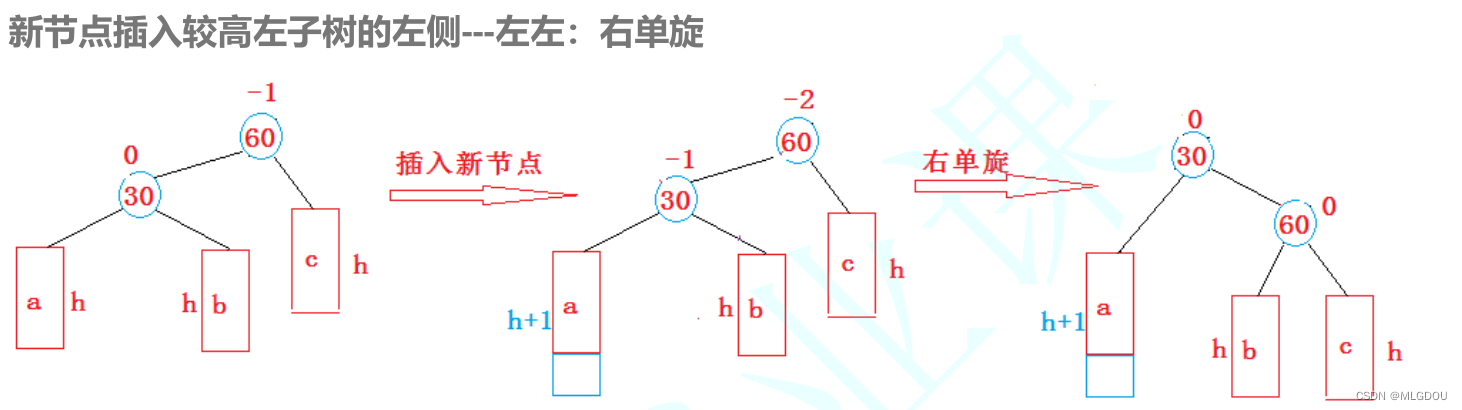
在这里插入图片描述

void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		Node* ppNode = parent->_parent;

		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;

		subL->_right = parent;
		parent->_parent = subL;

		if (ppNode == nullptr)
		{
			_root = subL;
			_root->_parent = nullptr;
		}
		else if(ppNode->_left==parent)
		{
			ppNode->_left = subL;
			subL->_parent = ppNode;
		}
		else
		{
			ppNode->_right = subL;
			subL->_parent = ppNode;
		}

		parent->_bf = subL->_bf = 0;

	}

左右双旋

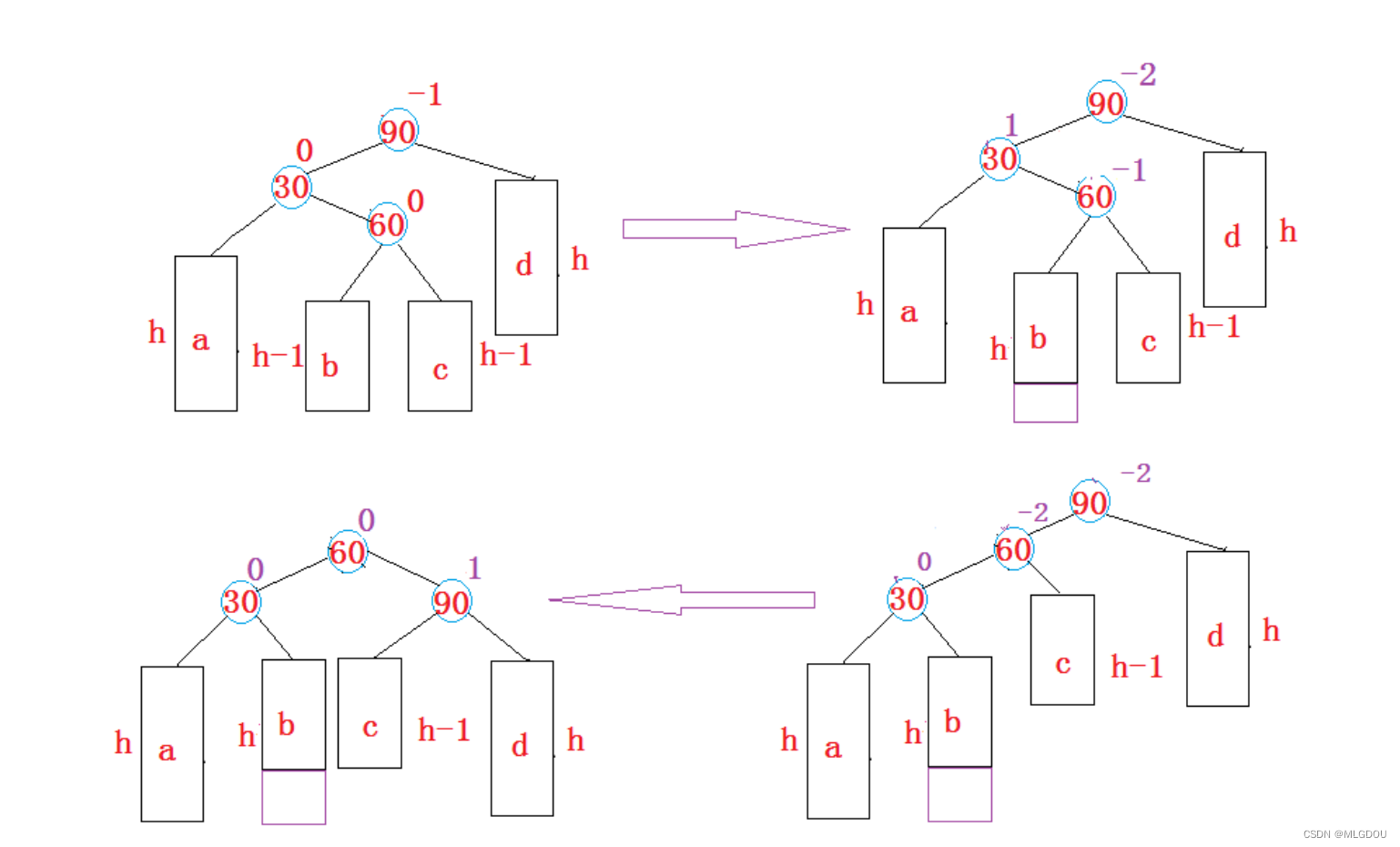
在这里插入图片描述
难点：平衡因子的调整
以上图为例，记录subLR初始的bf，然后分三种情况讨论即可

 void RotateLR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int bf = subLR->_bf;

		RotateL(parent->_left);
		RotateR(parent);

		if (bf == 1)
		{
			parent->_bf = 0;
			subLR->_bf = 0;
			subL->_bf = -1;
		}
		else if (bf == -1)
		{
			parent->_bf = 1;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subL->_bf = 0;
			subLR->_bf = 0;
		}

	}

右左双旋

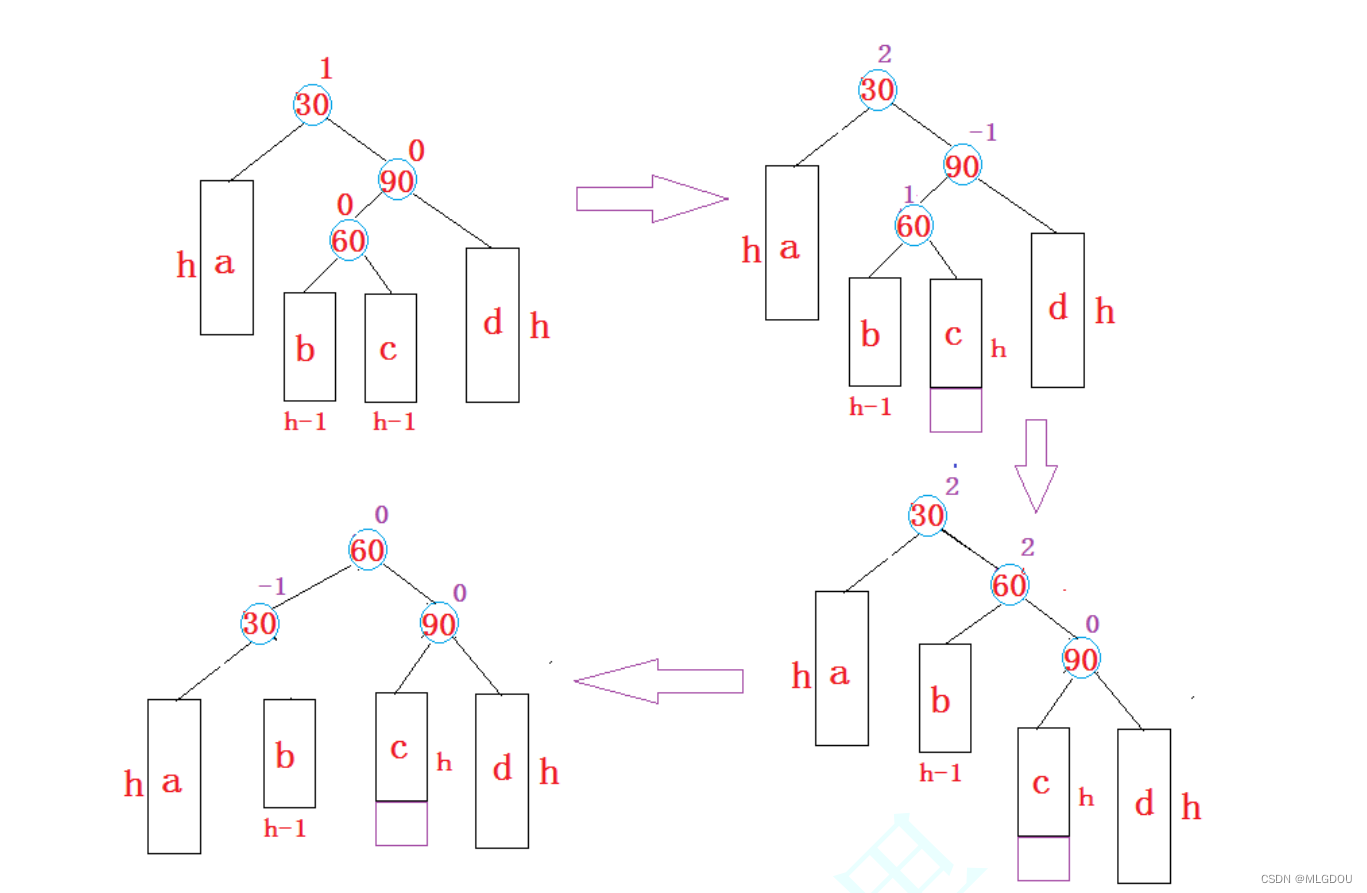
在这里插入图片描述

void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		int bf = subRL->_bf;

		RotateR(subR);
		RotateL(parent);

		if (bf == 1)
		{
			parent->_bf = -1;
			subRL->_bf = 0;
			subR->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 0;
			subRL->_bf = 0;
			subR->_bf = 1;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subRL->_bf = 0;
			subR->_bf = 0;
		}
		else
			assert(false);

	}

判断是否为平衡二叉树

bool IsBalance()
	{
		return _IsBalance(_root);
	}
bool _IsBalance(Node* root)
	{
		if (root == nullptr)
			return true;
		int lefth = _Height(root->_left);
		int righth = _Height(root->_right);

		if (righth - lefth != root->_bf)
		{
			cout << root->_kv.first << "节点平衡因子异常" << endl;
		}

		return abs(lefth - righth) < 2 && _IsBalance(root->_left)&&_IsBalance(root->_right);
	}

	int _Height(Node* root)
	{
		if (root == nullptr)
			return 0;
		int leftH = _Height(root->_left);
		int rightH = _Height(root->_right);
		return (leftH > rightH ? leftH : rightH) + 1;
	}

注意这里我们用递归获得子树的高度后，判断左右子树绝对值是否小于2还不行，还要逐层递归下去判断子树。

完整代码

#pragma once
#include<assert.h>
#include<iostream>
#include<time.h>

using namespace std;

template<class K,class V>
class AVLTreeNode
{
public:
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	pair<K, V> _kv;
	int _bf;

	AVLTreeNode(const pair<K,V>& kv)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_kv(kv)
		,_bf(0)
	{}
};

template<class K,class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
	bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(kv);
		if (kv.first > parent->_kv.first)
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}
		//父链接子，子要反向链接父
		cur->_parent = parent;

		//update bf
		while (parent)
		{
			if (cur == parent->_right)
			{
				parent->_bf++;
			}
			else
			{
				parent->_bf--;
			}

			if (parent->_bf == 1 || parent->_bf == -1)
			{
				parent = parent->_parent;
				cur = cur->_parent;
			}
			else if (parent->_bf == 0)
			{
				break;
			}
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				//rotate
				if (parent->_bf == 2 && cur->_bf == 1)
					RotateL(parent);
				else if (parent->_bf == -2 && cur->_bf == -1)
					RotateR(parent);
				else if (parent->_bf == -2 && cur->_bf == 1)
					RotateLR(parent);
				else if (parent->_bf == 2 && cur->_bf == -1)
					RotateRL(parent);
				else
					assert(false);
				break;

			}
			else
			{
				assert(false);
			}
		}

		return true;
	}

private:
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if(subRL)			
			subRL->_parent = parent;

		Node* ppNode = parent->_parent;

		subR->_left = parent;
		parent->_parent = subR;

		//判断上面是否有根
		if (ppNode == nullptr)
		{
			_root = subR;
			_root->_parent = nullptr;
		}
		else
		{
			if (ppNode->_left == parent)
			{
				ppNode->_left = subR;
				subR->_parent = ppNode;
			}
			else
			{
				ppNode->_right = subR;
				subR->_parent = ppNode;
			}
		}

		parent->_bf = subR->_bf = 0;
	}

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		Node* ppNode = parent->_parent;

		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;

		subL->_right = parent;
		parent->_parent = subL;

		if (ppNode == nullptr)
		{
			_root = subL;
			_root->_parent = nullptr;
		}
		else if(ppNode->_left==parent)
		{
			ppNode->_left = subL;
			subL->_parent = ppNode;
		}
		else
		{
			ppNode->_right = subL;
			subL->_parent = ppNode;
		}

		parent->_bf = subL->_bf = 0;
	}

	 void RotateLR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int bf = subLR->_bf;

		RotateL(parent->_left);
		RotateR(parent);

		if (bf == 1)
		{
			parent->_bf = 0;
			subLR->_bf = 0;
			subL->_bf = -1;
		}
		else if (bf == -1)
		{
			parent->_bf = 1;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subL->_bf = 0;
			subLR->_bf = 0;
		}

	}

	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		int bf = subRL->_bf;

		RotateR(subR);
		RotateL(parent);

		if (bf == 1)
		{
			parent->_bf = -1;
			subRL->_bf = 0;
			subR->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 0;
			subRL->_bf = 0;
			subR->_bf = 1;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subRL->_bf = 0;
			subR->_bf = 0;
		}
		else
			assert(false);

	}
public:
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}

	bool IsBalance()
	{
		return _IsBalance(_root);
	}

	
private:
	void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;
		_InOrder(root->_left);
		cout << root->_kv.first << " ";
		_InOrder(root->_right);
	}

	bool _IsBalance(Node* root)
	{
		if (root == nullptr)
			return true;
		int lefth = _Height(root->_left);
		int righth = _Height(root->_right);

		if (righth - lefth != root->_bf)
		{
			cout << root->_kv.first << "节点平衡因子异常" << endl;
		}

		return abs(lefth - righth) < 2 && _IsBalance(root->_left)&&_IsBalance(root->_right);
	}

	int _Height(Node* root)
	{
		if (root == nullptr)
			return 0;
		int leftH = _Height(root->_left);
		int rightH = _Height(root->_right);
		return (leftH > rightH ? leftH : rightH) + 1;
	}
private:
	Node* _root=nullptr;
};

void Test_AVLTree1()
{
	int a[] = { 16,3,7,11,9,26,18,14,15 };
	AVLTree<int, int> t1;
	for (int e : a)
	{
		t1.Insert(make_pair(e,e));
	}

	t1.InOrder();
	cout<<t1.IsBalance();
}

//生成随机数测试
void Test_AVLTree2()
{
	srand(time(0));
	const size_t N = 10000;
	AVLTree<int, int> t;
	for (size_t i = 0; i < N; i++)
	{
		size_t x = rand();
		t.Insert(make_pair(x, x));
		//cout << t.IsBalance() << endl;
	}
	cout << t.IsBalance() << endl;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1488122.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Mybatis框架相关问题

Mybatis框架相关问题

HashMap相关问题 Mybatis框架相关问题 一、MyBatis框架是如何实现分页的&#xff1f;二、MyBatis框架里面的缓存机制是怎么回事&#xff1f;一级缓存二级缓存 一、MyBatis框架是如何实现分页的&#xff1f; 分页分为两种&#xff1a; 逻辑分页&#xff1a;将所有数据查询出来…
阅读更多...
CBA全明星急需改革但先不谈！不如先学学如何尊重球迷

CBA全明星急需改革但先不谈！不如先学学如何尊重球迷

直播吧指定地址&#xff1a;www.bjcenn.com 3月4日讯 昨晚CBA全明星正赛&#xff0c;南区明星队138-122击败北区明星队。 媒体人三土带刺更博长文总结了本次全明星&#xff0c;原文如下&#xff1a; 如何总结这次全明星&#xff1f; 又一届CBA全明星周末结束&#xff0c;关…
阅读更多...
9.10目标和（LC494-M）

9.10目标和（LC494-M）

算法&#xff1a; 加法的绝对值的集合left 减法的绝对值的集合right nums集合的总和sum 这里的left和right都是绝对值&#xff1a; leftrightsum → rightsum-left left-righttarget → left-(sum-left) target → left (target sum)/2 &#xff0c;target …
阅读更多...
充电桩组装行业生产管理MES系统解决方案

充电桩组装行业生产管理MES系统解决方案

充电桩组装行业MES系统是一个综合生产管理系统&#xff0c;融合了工厂企业必要的销售、物流和制造管理等全公司基础业务以及生产计划和现场监测管理。通过结合工业物联网(IIoT)解决方案&#xff0c;将所有重要生产设备进行关联&#xff0c;实现工厂数字化、可视化管理。通过系统…
阅读更多...
云计算 2月28号 （linux的磁盘分区）

云计算 2月28号 （linux的磁盘分区）

一 存储管理 主要知识点: 基本分区、逻辑卷LVM、EXT3/4/XFS文件系统、RAID 初识硬盘 机械 HDD 固态 SSD SSD的优势 SSD采用电子存储介质进行数据存储和读取的一种技术&#xff0c;拥有极高的存储性能&#xff0c;被认为是存储技术发展的未来新星。 与传统硬盘相比&#xff0c…
阅读更多...
Python - getpass

Python - getpass

文章目录 关于 getpass基本使用语法说明其它 关于 getpass getpass 是 Python 自带标准库 Python 官方文档 - getpass https://docs.python.org/3/library/getpass.html 基本使用 我们在看视频教程中&#xff0c;老师如果不想在代码中暴露 token、密码之类的信息&#xff0c…
阅读更多...
day03_Vue_Element

day03_Vue_Element

文章目录 01.Ajax1.1 Ajax 概述1.2 同步异步1.3 原生Ajax 2. Axios2.1 Axios的基本使用2.2 Axios快速入门2.3请求方法的别名2.4 案例 3 前后台分离开发3.1 前后台分离开发介绍 04 YAPI4.1 YAPI介绍4.2 接口文档管理 05 前端工程化5.1 前端工程化介绍5.2 前端工程化入门5.2.1 环…
阅读更多...
深度学习GPU环境安装（WINDOWS安装NVIDIA）

深度学习GPU环境安装（WINDOWS安装NVIDIA）

1.检测是否支持GPU环境 1.1.打开设备管理器 winows下面搜索设备管理器&#xff08;或者从桌面"此电脑"——>右键点击——>"管理"打开&#xff09; 1.2.查看本地显卡 在"设备管理器"——"显示适配器"中&#xff0c;如果没有&…
阅读更多...
Jupyter Notebook运行Python代码如何传参

Jupyter Notebook运行Python代码如何传参

在Jupyter Notebook中&#xff0c;运行Python源代码非常方便&#xff0c;但是如何模拟命令行方式运行时的输入参数呢&#xff1f; 如果直接使用sys.argv会出现错误。例如使用argv[1]时出现&#xff1a; 导致上述错误的原因为&#xff1a;在Jupyter Notebook中运行Python代码时&…
阅读更多...
python--开心篇--print--多种多样的print输出

python--开心篇--print--多种多样的print输出

文章目录 名言输出绕口令输出《水浒传》中的梁山好汉输出轨道交通充值信息输出对联字符画输出长春地铁1号线运行图模拟12306查询界面模拟企业网站登录界面 名言 print("& "*15) print("& &") print("& …
阅读更多...
还在犹豫学不学？鸿蒙技术是否有前途的最强信号来了

还在犹豫学不学？鸿蒙技术是否有前途的最强信号来了

2024年3月3日 上午10 点&#xff0c;深圳官方账号发布了一篇关于鸿蒙技术发展的重要文章&#xff0c;看到这篇文章后我非常激动&#xff0c;忍不住和大家分享一下&#xff01; 华为鸿蒙系统自提出以来&#xff0c;网友们的态度各不相同&#xff0c;有嘲笑“安卓套壳”的&#x…
阅读更多...
SpringBoot整合rabbitmq-重复消费问题

SpringBoot整合rabbitmq-重复消费问题

说明&#xff1a;重复消费的原因大致是生产者将信息A发送到队列中&#xff0c;消费者监听到消息A后开始处理业务&#xff0c;业务处理完成后&#xff0c;监听在告知rabbitmq消息A已经被消费完成途中中断&#xff0c;也就时说我已经处理完业务&#xff0c;而队列中还存在当前消息…
阅读更多...
动态规划DP之背包问题4---分组背包问题

动态规划DP之背包问题4---分组背包问题

目录 DP分析&#xff1a; 例题&#xff1a; 01背包&#xff1a; 一种物品只有一件 动态规划DP之背包问题1---01背包问题-CSDN博客 完全背包&#xff1a;一种物品有无限件 动态规划DP之背包问题2---完全背包问题-CSDN博客 多重背包&#xff1a;一种物品有有限…
阅读更多...
Avalonia学习（二十九）-仪表

Avalonia学习（二十九）-仪表

Avalonia制作仪表盘&#xff0c;把控件给大家演示一下&#xff0c;Avalonia有三类自定义控件&#xff0c;分别是用户控件、模版控件、自主控件。前面已经很多用户控件了&#xff0c;这个是演示模版控件&#xff0c;另外一种不知道哪种情况下使用。 前端代码&#xff1a; <…
阅读更多...
常用的java反编译工具介绍

常用的java反编译工具介绍

在软件开发和逆向工程领域&#xff0c;反编译工具是一个重要的工具&#xff0c;它们可以帮助开发者理解、分析和修改编译后的Java字节码文件&#xff08;.class文件&#xff09;。这些工具通常用于以下几个目的&#xff1a; 1. 调试&#xff1a;帮助开发者理解字节码的…
阅读更多...
CloudCanal x Hive 构建高效的实时数仓

CloudCanal x Hive 构建高效的实时数仓

简述 CloudCanal 最近对于全周期数据流动进行了初步探索&#xff0c;打通了Hive 目标端的实时同步&#xff0c;为实时数仓的构建提供了支持&#xff0c;这篇文章简要做下分享。 基于临时表的增量合并方式基于 HDFS 文件写入方式临时表统一 Schema任务级的临时表 基于临时表的…
阅读更多...
华为手环 8：返校季新宠，助力高效学习与健康生活

华为手环 8：返校季新宠，助力高效学习与健康生活

随着春节假期的结束&#xff0c;学生们也纷纷踏上了返校的旅途。新的学期&#xff0c;新的气象&#xff0c;让华为手环8为你的带来全新的智能生活体验。它不仅仅是一款风格多变的时尚手环&#xff0c;还拥有了智能消息提醒、100多种运动模式和睡眠监测等强大功能&#xff0c;让…
阅读更多...
Linux 实现打印彩色进度条

Linux 实现打印彩色进度条

文章目录 预备知识一、理解回车换行二、认识行缓冲1、代码一、二&#xff08;回车换行理解&#xff09;2、代码三、四&#xff08;sleep函数和ffush函数理解&#xff09; 三、简单倒计时1. 倒计时代码2、效果展示 四、进度条1、效果展示2、进度条代码makefileProcessBar.hProce…
阅读更多...
【数据结构和算法初阶(C语言)】双向循环带头链表的增删查改详解（天才设计的链表结构，应用简单逆天！！！！！）

【数据结构和算法初阶(C语言)】双向循环带头链表的增删查改详解（天才设计的链表结构，应用简单逆天！！！！！）

目录 ​编辑​编辑 1.双向链表的定义&#xff1a;前赴后继 2.带头链表的定义-----哨兵位 3.增删查改 3.1创建新节点函数----方便后续增加节点调用 3.2创建哨兵位----创建头结点 3.3增加节点&#xff0c;尾部插入数据 3.4尾删除 3.5查找函数----遍历对比&#xff…
阅读更多...
程序人生：当看到男友学测试拿高薪后，我突然悟了......

程序人生：当看到男友学测试拿高薪后，我突然悟了......

Hello&#xff0c;大家好&#xff0c;我是小雨 认识软件测试是因为我男朋友&#xff0c;他在华测教育培训软测后出去就业非常不错&#xff0c;所以我也萌生了转行的想法&#xff0c;当时我的想法是&#xff0c;他都能学会&#xff0c;那我肯定没问题&#xff0c;所以在他的介绍…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023