目录

 DP分析：

例题：

---

        01背包：   一种物品只有一件         动态规划DP之背包问题1---01背包问题-CSDN博客

        完全背包：一种物品有无限件         动态规划DP之背包问题2---完全背包问题-CSDN博客

        多重背包：一种物品有有限的个数  动态规划DP之背包问题3---多重背包问题-CSDN博客

        分组背包：有一组物品，每组物品中只能选一个 

有 N 组物品和一个容量是 V 的背包。

每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是 ，价值是 ，其中 i 是组号，j 是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

 DP分析：

        只要掌握前三种背包问题，分组背包就很简单了。

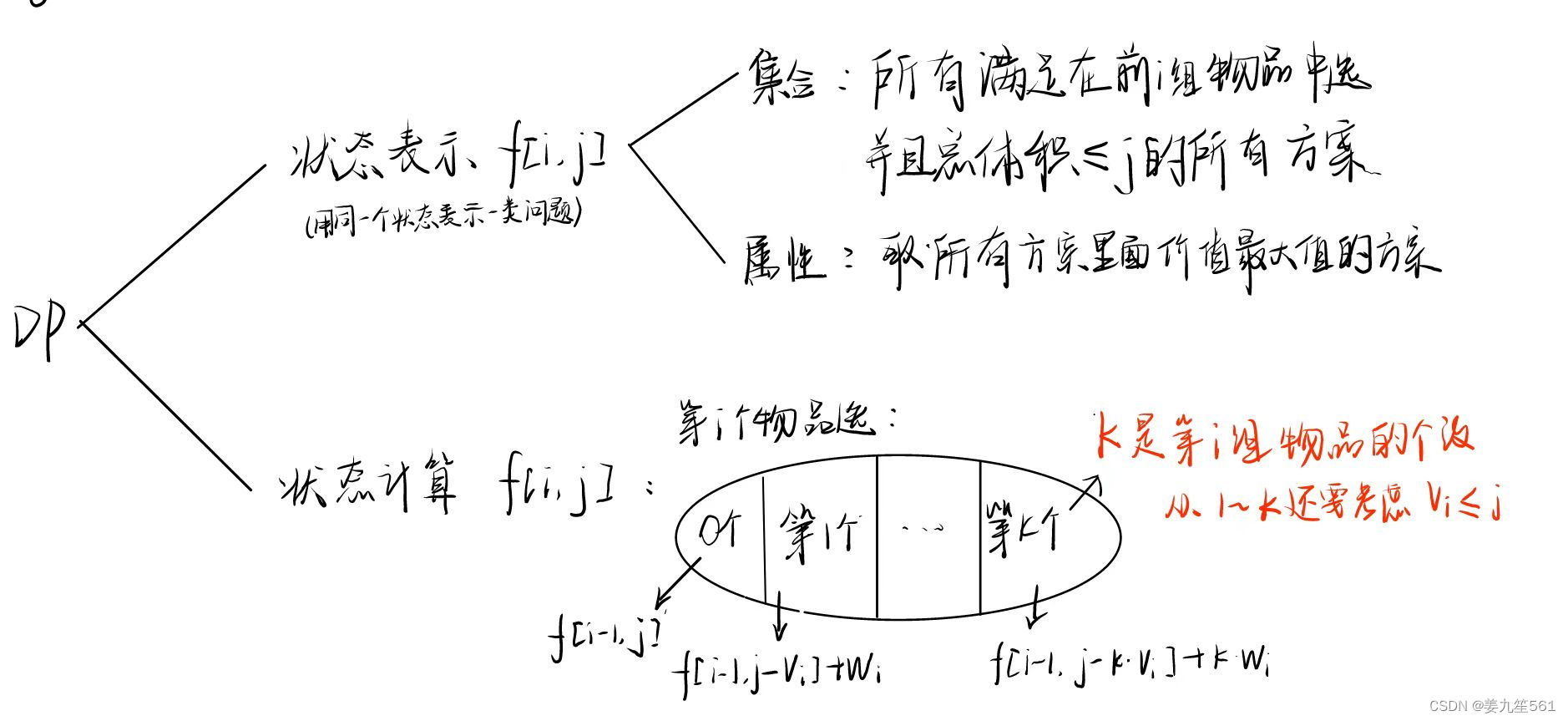
        代码（一维）：

for(int i=1;i<=n;i++)
    for(int j=V;j>=0;j--)
        for(int k=1;k<=s[i];k++) // 循环第i组物品的个数
            if(v[i][k]<=j) 
                f[j] = Math.max(f[j],f[j-v[i][k]]+w[i][k]);     

例题：

有 N 组物品和一个容量是 V 的背包。

每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是 vij，价值是 wij，其中 i 是组号，j 是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式

第一行有两个整数 N，V，用空格隔开，分别表示物品组数和背包容量。

接下来有 N 组数据：

• 每组数据第一行有一个整数 Si，表示第 i 个物品组的物品数量；
• 每组数据接下来有 Si 行，每行有两个整数 vij,wij，用空格隔开，分别表示第 i 个物品组的第 j 个物品的体积和价值；

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤100
0<Si≤100
0<vij,wij≤100

输入样例

3 5
2
1 2
2 4
1
3 4
1
4 5

输出样例：

8

import java.util.*;

class Main{
    static final int N = 110;
    static int n,m;
    static int[][] v = new int[N][N]; // 表示第i组物品中第j个物品的体积
    static int[][] w = new int[N][N]; // 表示第i组物品中第j个物品的价值
    static int[] s = new int[N]; // 第i组物品的个数
    static int[] f = new int[N]; // 存放dp结果，状态
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        m = in.nextInt();
        for(int i=1;i<=n;i++){
            s[i] = in.nextInt();
            for(int j=1;j<=s[i];j++){
                v[i][j] = in.nextInt();
                w[i][j] = in.nextInt();
            }
        }
        for(int i=1;i<=n;i++){
            for(int j=m;j>=0;j--){
                for(int k=1;k<=s[i];k++){ // 循环第i组物品的个数
                    if(v[i][k]<=j) f[j] = Math.max(f[j],f[j-v[i][k]]+w[i][k]);                    
                }

            }
        }
        System.out.println(f[m]);
      
    }
}