9.10目标和（LC494-M）

news2024/9/24 5:24:49

算法：

加法的绝对值的集合left

减法的绝对值的集合right

nums集合的总和sum

这里的left和right都是绝对值：

left+right=sum → right=sum-left

left-right=target → left-(sum-left) =target

→ left = (target + sum)/2 ，target 和sum都是常量

若target + sum为奇数，则无法整除，其实实际意义就是，没有组合能够得到目标和target。

这道题可以用回溯，也可以用01背包。

此时问题就转化为，装满容量为left的背包，有几种方法。

为什么是01背包呢？

因为每个物品（示例1中的1）只用一次！

这次和之前遇到的背包问题不一样了，之前都是求容量为j的背包，最多能装多少。

本题则是装满有几种方法。其实这就是一个组合问题了。

动规五部曲：

1.确定dp数组及其下标

dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法

2.确定递推公式

例如：dp[j]，j 为5，

已经有一个1（nums[i]）的话，有 dp[4]种方法凑成容量为5的背包。
已经有一个2（nums[i]）的话，有 dp[3]种方法凑成容量为5的背包。
已经有一个3（nums[i]）的话，有 dp[2]中方法凑成容量为5的背包
已经有一个4（nums[i]）的话，有 dp[1]中方法凑成容量为5的背包
已经有一个5 （nums[i]）的话，有 dp[0]中方法凑成容量为5的背包

那么凑整dp[5]有多少方法呢，也就是把 所有的 dp[j - nums[i]] 累加起来。

求组合类问题的公式，都是类似这种：

dp[j] += dp[j - nums[i]]

3.dp数组初始化

从递推公式可以看出，在初始化的时候dp[0] 一定要初始化为1，因为dp[0]是在公式中一切递推结果的起源，如果dp[0]是0的话，递推结果将都是0。

举个例子：

如果数组[0] ，target = 0，那么 bagSize = (target + sum) / 2 = 0。 dp[0]也应该是1，也就是说给数组里的元素 0 前面无论放加法还是减法，都是 1 种方法。

所以本题我们应该初始化 dp[0] 为 1。

4.确定遍历顺序

nums放在外循环，target在内循环，且内循环倒序。

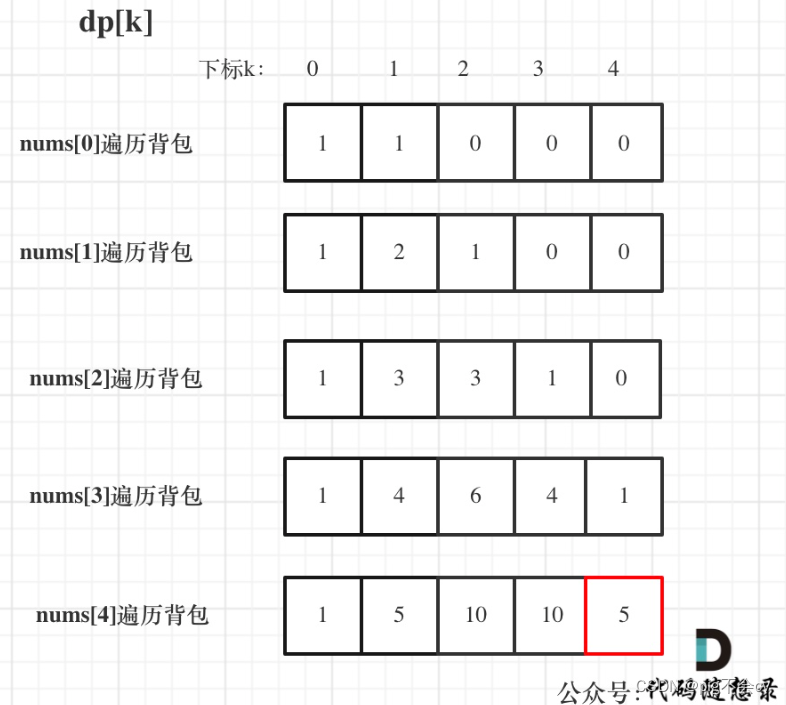
5.举例推导dp数组

输入：nums: [1, 1, 1, 1, 1], S: 3

bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4

正确代码：

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int sum = 0;
        for(int i=0; i<nums.length; i++){
            sum += nums[i];
        }
        if ((sum+target)%2 != 0) return 0;
        if (target <0 && sum <-target) return 0;

        int bagsize = (sum+target)/2;
        if (bagsize<0){
            bagsize = -bagsize;
        }
        int[] dp = new int[bagsize+1];
        dp[0] = 1;
        for (int i=0; i<nums.length; i++){
            for(int j=bagsize; j>=nums[i]; j--){
                dp[j] += dp[j-nums[i]];
            }
        }
        return dp[bagsize];


    }
}