【CSP试题回顾】201709-1-打酱油
news2026/2/13 9:53:51
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1487093.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
品牌作为储蓄池:静态积累与长期价值
在瞬息万变的商业环境中,品牌不仅仅是一个简单的标识或名字,它更像是一个融合了静态积累与长期价值的综合储蓄池。品牌通过不断的积累,建立起深厚的市场基础和消费者信任,这些无形的资产为品牌的长期发展奠定了坚实的基础。品牌推…
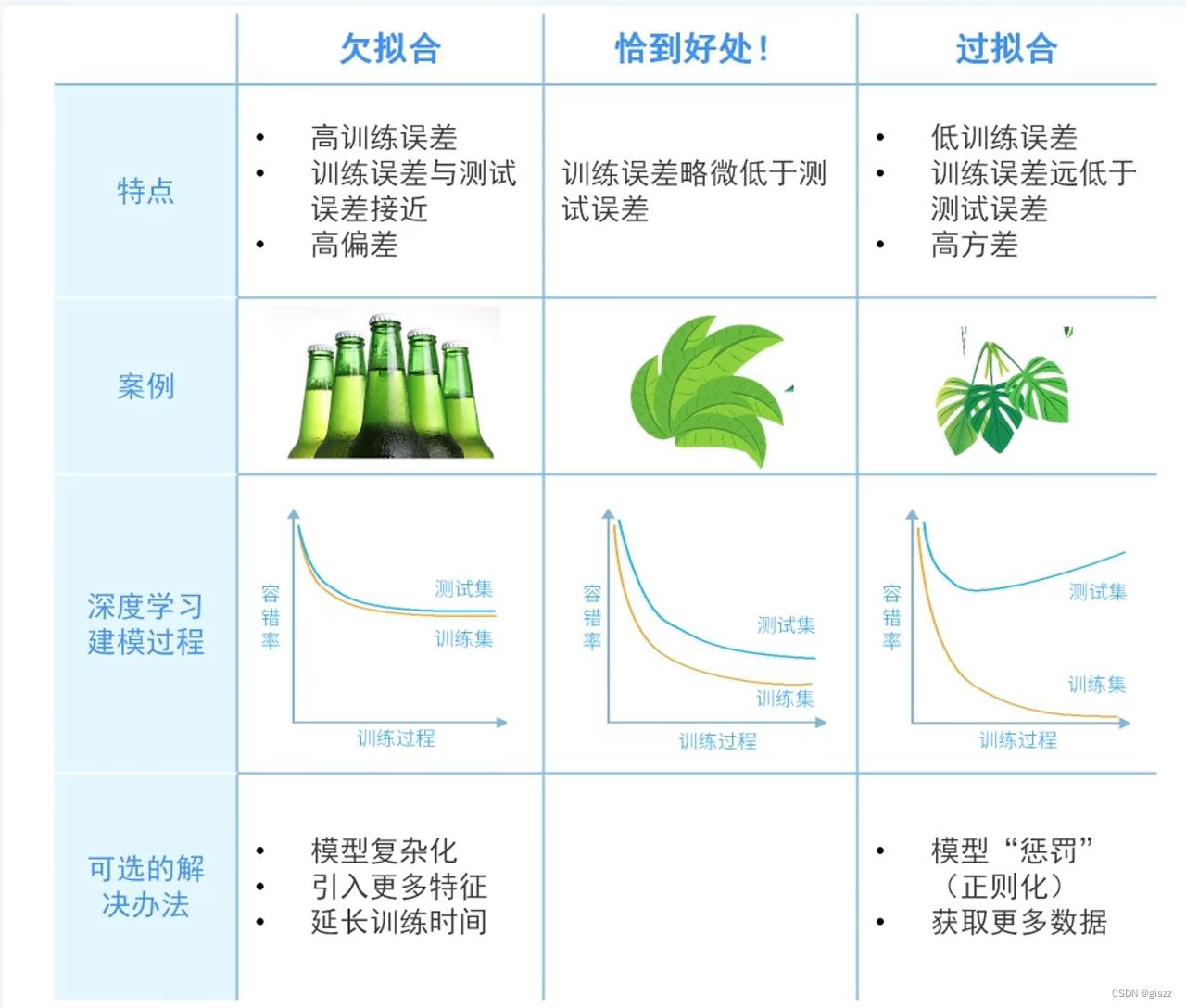
【大厂AI课学习笔记NO.59】(12)过拟合与欠拟合
拟合就是调整参数和模型,让结果无限接近真实值的过程。 我们先来了解个概念:
偏差-方差窘境(bias-variance dilemma)是机器学习中的一个重要概念,它涉及到模型选择时面临的权衡问题。
偏差(Bias…
【二分查找】【C++算法】378. 有序矩阵中第 K 小的元素
作者推荐
视频算法专题
本文涉及的基础知识点
二分查找算法合集
LeetCode378. 有序矩阵中第 K 小的元素
给你一个 n x n 矩阵 matrix ,其中每行和每列元素均按升序排序,找到矩阵中第 k 小的元素。 请注意,它是 排序后 的第 k 小元素&…
ubuntu安裝Avahi发现服务工具
一、简介
解决设置固定ip后无法连接外网的问题,目前采用动态获取ip,可以不用设置设备的固定IP,直接可以通过域名来访问设备,类似树莓派的连接调试
二、安装
本文使用的是ubuntu23.10.1上安装 1.安装工具
sudo apt install av…
展览展会媒体传播的必要性,有哪些宣传方式?
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。
展览展会媒体传播的必要性在于扩大影响力、吸引观众和促进行业交流。通过媒体宣传,可以快速传递展会信息,提升品牌知名度,吸引更多潜在参展商和观众。…
【C语言】linux内核packet_setsockopt
一、中文注释
// 发送数据包函数。它尝试通过特定的网络设备队列直接传输一个skb(socket缓冲区)。
static int packet_direct_xmit(struct sk_buff *skb)
{return dev_direct_xmit(skb, packet_pick_tx_queue(skb)); // 调用dev_direct_xmit函数&#x…
上位机图像处理和嵌入式模块部署(上、下位机通信的三个注意点)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 如果最终部署在客户现场的是一个嵌入式设备,那么上位机在做好了算法编辑和算法部署之后,很重要的一步就是处理上位机和下位…
Intel FPGA IP之LVDS SerDes IP学习
FPGA 视频数据输入输出直通工程:
屏:13.2吋8bit色深,屏幕分辨率为1440*192060,具有两个Port,每个Port有4个差分数据对与1个差分时钟对,差分对均支持LVDS协议芯片:Cyclone V系列FPGA目的&#x…
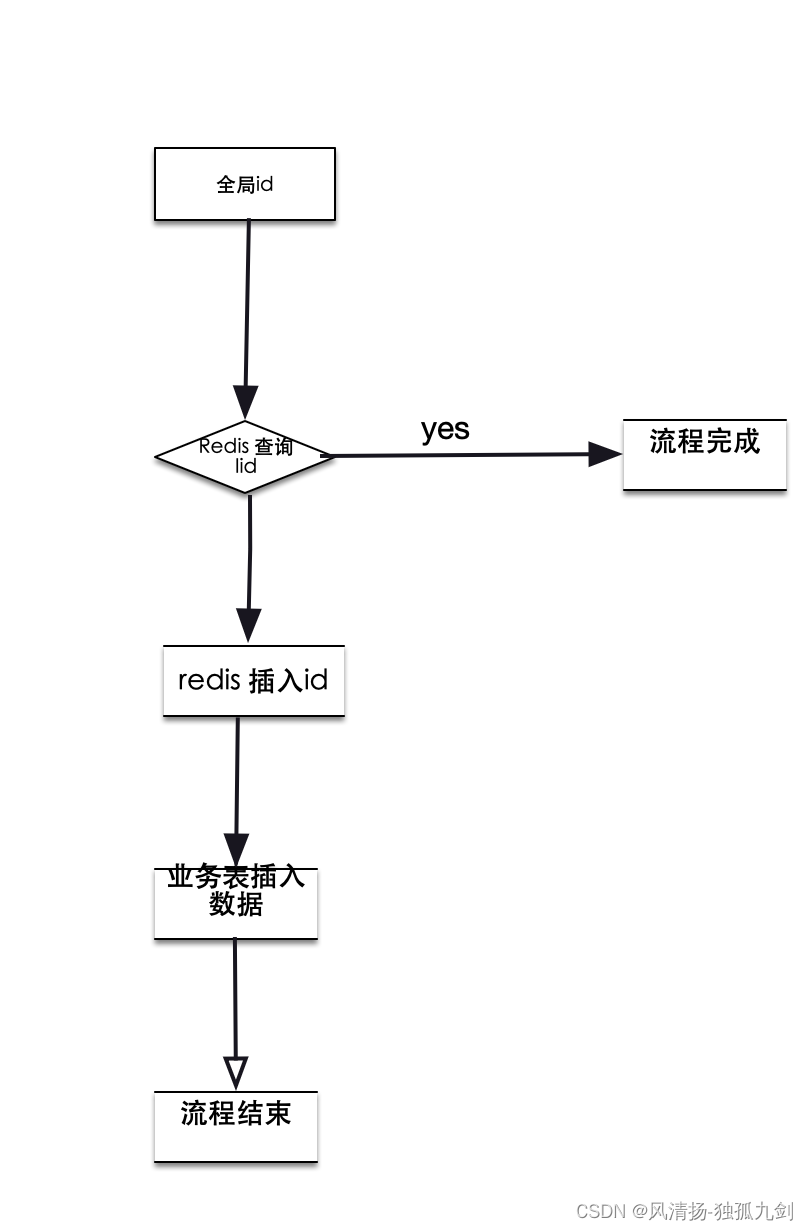
分布式ID生成策略-雪花算法Snowflake
分布式ID生成策略-雪花算法Snowflake 一、其他分布式ID策略1.UUID2.数据库自增与优化2.1 优化1 - 共用id自增表2.2 优化2 - 分段获取id 3.Reids的incr和incrby 二、雪花算法Snowflake1.雪花算法的定义2.基础雪花算法源码解读3.并发1000测试4.如何设置机房和机器id4.雪花算法时钟…
在Ubuntu22.04安装Fcitx5中文输入法教程(十分详细)
前言
书接上回,一时兴起将主力机的 Ubuntu 20.04 LTS 升级至了刚刚发布的 22.04 LTS。从 X 切换到 Wayland 、GNOME 从 3.36 升级至 42、Python 默认为 3.10 等等……使用太新的软件包反而暂时带来了麻烦,部分原有的软件和插件都不可用了。这其中就包括…
浅谈马尔科夫链蒙特卡罗方法(MCMC)算法的理解
1.解决的问题
计算机怎么在任意给定的概率分布P上采样?首先可以想到把它拆成两步:
(1)首先等概率的从采样区间里取一个待定样本x,并得到它的概率为p(x)
(2)然后在均匀分布U[0,1]上取一个值&a…
可视化管理的kanban插件 | Obsidian实践
继上一篇文章之后,有朋友提问说: 刚好,关于kanban插件的素材,是之前一早就准备好的,便快速整理成文,简单分享一下个人实践。 Prompt:项目流程管理看板,色彩鲜艳。by 通义万象 看板管…
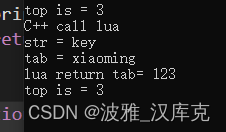
C++调用lua函数
C 调用Lua全局变量(普通) lua_getglobal(lua, "width");int width lua_tointeger(lua,-1);lua_pop(lua,1);std::cout << width << std::endl;lua_close(lua);
这几行代码要放到lua_pcall(lua, 0,0,0);之后才可以. C给lua传递变量 lua_pushstring(lua, …
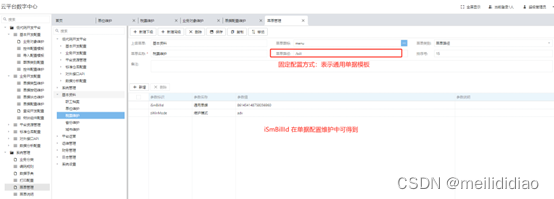
三、低代码平台-单据配置(单表增删改查)
一、业务效果图 主界面 二、配置过程简介 配置流程:业务表设计 -》业务对象建立-》业务单据配置-》菜单配置。 a、业务表设计 b、业务对象建立 c、业务单据配置
功能路径:低代码开发平台/业务开发配置/单据配置维护 d、菜单配置
【JavaEE】_Spring MVC 项目传参问题
目录 1. 传递单个参数
1.1 关于参数名的问题
2. 传递多个参数
2.1 关于参数顺序的问题
2.2 关于基本类型与包装类的问题
3. 使用对象传参
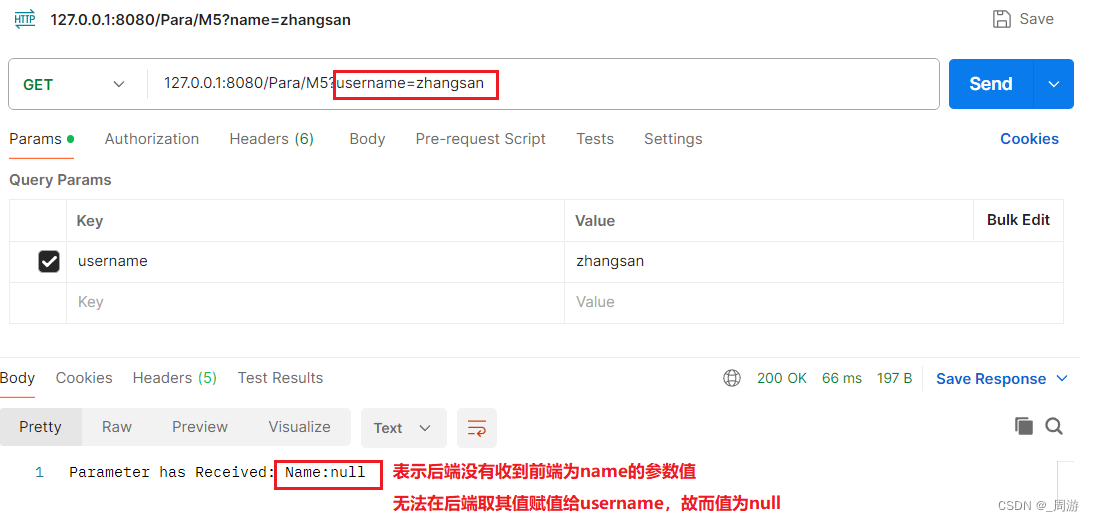
4. 后端参数重命名问题
4.1 关于RequestPara注解 1. 传递单个参数
现创建Spring MVC项目,.java文件内容如下ÿ…
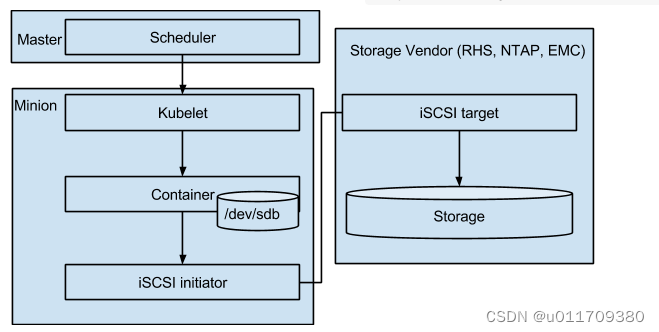
【k8s存储--使用OpenEBS做持久化存储】
1、简介
使用OpenEBS,你可以将有持久化数据的容器,像对待其他普通容器一样来对待。OpenEBS本身也是通过容器来部署的,支持Kubernetes、Swarm、Mesos、Rancher编排调度,存储服务可以分派给每个pod、应用程序、集群或者容器级别&am…
Mybatis plus拓展功能-JSON处理器
目录
1 前言
2 使用方法
2.1 定义json实体类
2.2 在实体类中使用 1 前言
这是我最近学到的比较新奇的一个东西,数据库居然还可以存储JSON格式的数据,如下。虽然我感觉一般也没谁会这样干,但是既然有,那就当个科普讲一下Mybat…
【自然语言处理】NLP入门(三):1、正则表达式与Python中的实现(3):字符转义符及进制转换
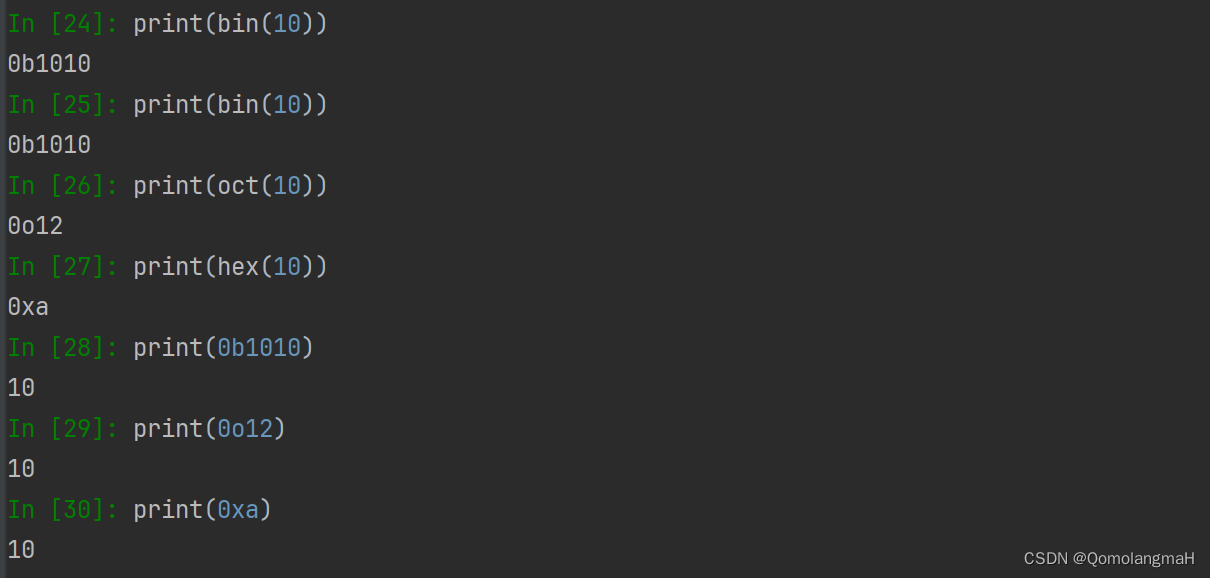
文章目录 一、前言二、正则表达式与Python中的实现1.字符串构造2. 字符串截取3. 字符串格式化输出4. 字符转义符a. 常用字符转义符续行符换行符制表符双引号单引号反斜杠符号回车符退格符 b. ASCII编码转义字符进制转换2 进制8 进制10 进制16 进制进制转换函数 c. Unicode字符\…
每天学习一个Linux命令之gunzip
每天学习一个Linux命令之gunzip 在Linux系统中,有许多强大且常用的命令,其中之一是gunzip。gunzip命令用于解压缩.gz文件,它是gzip的伴生命令之一。本篇博客将详细介绍gunzip命令及其可用的选项,以帮助您更好地理解和使用这个命令…