拟合就是调整参数和模型，让结果无限接近真实值的过程。

我们先来了解个概念： 

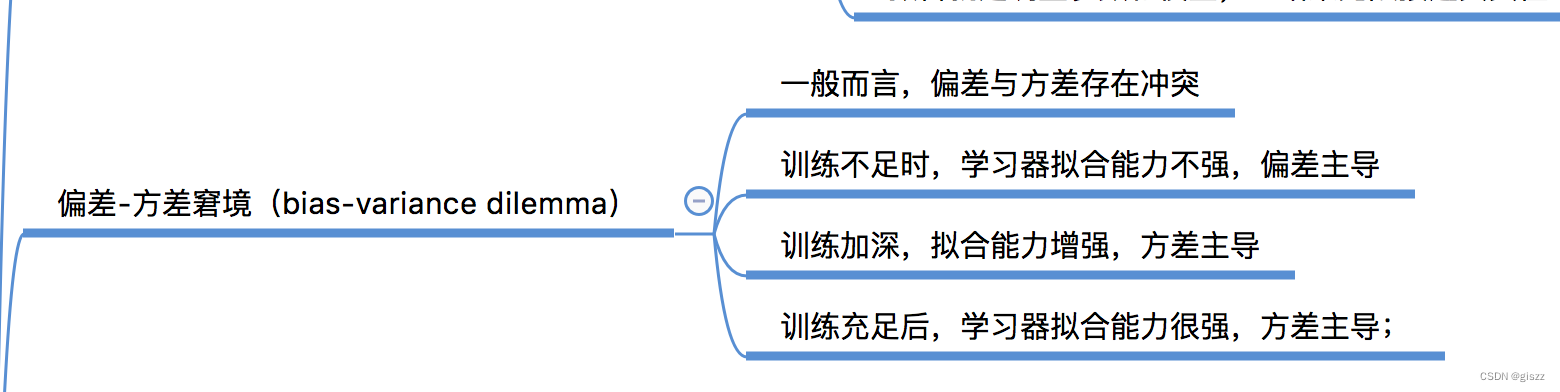
偏差-方差窘境（bias-variance dilemma）是机器学习中的一个重要概念，它涉及到模型选择时面临的权衡问题。

偏差（Bias）度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力。当模型过于简单，无法捕捉到数据的所有复杂性时，就会出现高偏差的情况，此时模型可能会欠拟合（underfit）数据。

方差（Variance）则度量了在同样大小的训练集的变动下，学习性能的变化，即刻画了数据扰动所造成的影响。当模型过于复杂，对训练数据中的噪声和特定细节过于敏感时，就会出现高方差的情况，此时模型可能会过拟合（overfit）数据。

在模型选择时，我们通常会面临偏差和方差之间的权衡。简单的模型可能具有较高的偏差和较低的方差，而复杂的模型可能具有较低的偏差和较高的方差。因此，在选择模型时，我们需要找到一个平衡点，使得模型既能够捕捉到数据的内在规律，又不会对数据中的噪声和特定细节过于敏感。

偏差-方差窘境的存在意味着我们无法同时最小化偏差和方差。在实际应用中，我们通常需要借助交叉验证、正则化等技术来平衡偏差和方差，从而选择出最优的模型。

需要注意的是，除了偏差和方差之外，还有一个重要的因素也会影响模型的性能，那就是噪声（Noise）。噪声表达了在当前任务上任何算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度。因此，在实际应用中，我们还需要考虑噪声对模型性能的影响。

泛化性能是由学习算法的能力，数据的充分性，以及学习任务共同难度决定了。

之前讲过，在此不再赘述。

我们再学习一个概念：偏差-方差分解（bias-variance decomposition）

偏差-方差分解（Bias-Variance Decomposition）是机器学习中一种重要的分析技术，用于解释学习算法泛化性能的一种工具。给定学习目标和训练集规模，它可以把一种学习算法的期望误差分解为三个非负项的和，即样本真实噪音（Noise）、偏差（Bias）和方差（Variance）。

• 样本真实噪音：是任何学习算法在该学习目标上的期望误差的下界，即刻画了学习问题本身的难度。这是由数据本身的特性所决定的，无法通过优化模型来减少。
• 偏差：度量了某种学习算法的平均估计结果所能逼近学习目标的程度，即刻画了模型的拟合能力和准确性。偏差越小，说明模型的拟合能力越强，预测结果越接近真实值。
• 方差：度量了在面对同样规模的不同训练集时，学习算法的估计结果发生变动的程度，即刻画了模型对数据扰动的敏感性。方差越小，说明模型对数据扰动的鲁棒性越强，不会因为训练集的微小变化而导致预测结果的剧烈波动。

需要注意的是，偏差和方差通常是相互矛盾的，即偏差的减小可能导致方差的增加，反之亦然。因此，在选择模型时，需要综合考虑偏差和方差之间的平衡，以及噪声对模型性能的影响，从而选择出最优的模型。

总的来说，偏差-方差分解提供了一种从偏差和方差的角度来解释学习算法泛化性能的方法，有助于我们更好地理解模型的性能表现，并指导我们进行模型选择和优化。

好，我们来了解过拟合与欠拟合。 

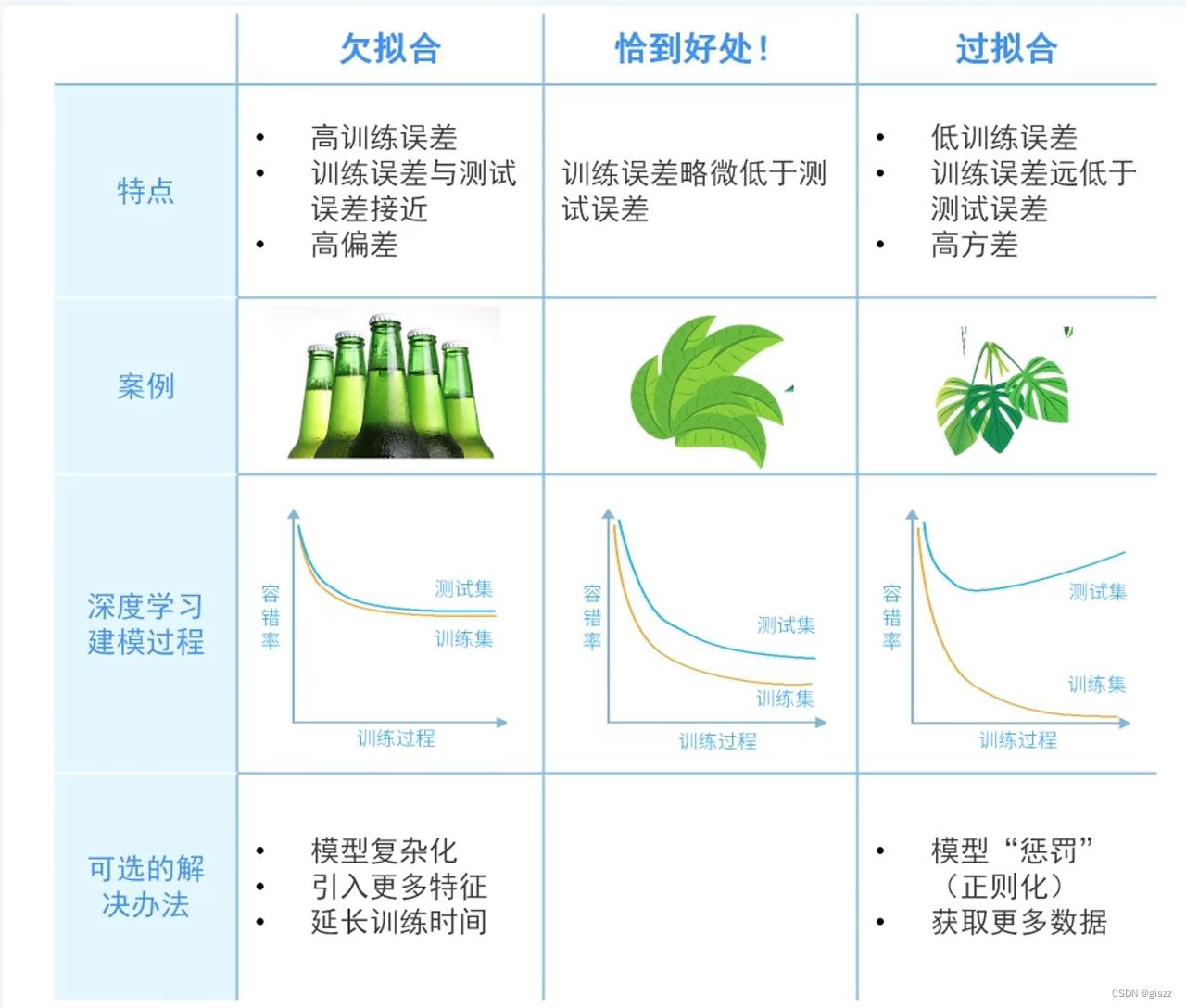
过拟合和欠拟合是机器学习和人工智能领域中两种常见的问题，它们描述了模型在训练数据和新数据上的表现差异。理解这两种现象对于构建有效的模型至关重要。

过拟合：

定义：过拟合是指模型在训练数据集上表现良好，但在测试数据集上表现较差。这通常是因为模型过于复杂，以至于它学到了训练数据中的噪声或特定特征，而没有学到真实的、可以泛化到新数据的规律。

原理：在训练过程中，模型的参数（特别是权重）被过度拟合，导致模型无法区分真实世界中的数据点和噪声。模型变得对训练数据过于敏感，失去了泛化到新数据的能力。

使用场景：过拟合通常发生在模型复杂度过高，或者训练数据量不足的情况下。例如，在图像识别任务中，如果模型参数过多，而训练图像数量有限，就容易出现过拟合。

避免方法：

1. 增加训练样本数量：通过收集更多的数据或使用数据增强的技术来增加训练样本的数量，可以帮助模型学习到更多的真实规律，减少过拟合。
2. 简化模型结构：适当降低模型的复杂度，如减少网络层数、神经元个数等，可以降低模型对训练数据中的噪声的敏感性。
3. 使用权重正则化：在损失函数中加入对权重的惩罚项，如L1正则化或L2正则化，可以限制模型参数的规模，防止过拟合。
4. 使用dropout：在训练过程中随机“关闭”一部分神经元，可以减少模型的参数数量，从而降低过拟合的风险。
5. 数据扩增：通过对训练数据进行变换（如旋转、平移、缩放等）来人为地增加数据量，提高模型的泛化能力。

欠拟合：

定义：欠拟合指的是模型无法充分学习训练集的规律，导致模型在训练集和测试集上表现都不佳。这通常是因为模型过于简单，无法捕捉到数据中的所有关系和结构。

原理：模型的复杂度不足以捕捉数据的内在规律，导致模型在训练和预测时都表现不佳。欠拟合的模型具有较高的偏差（bias），这意味着它们在预测时会倾向于产生较大的误差。

使用场景：欠拟合通常发生在模型复杂度过低，或者特征选择不当的情况下。例如，在文本分类任务中，如果仅使用简单的词袋模型而忽略词序和语义信息，就容易出现欠拟合。

避免方法：

1. 添加新特征：当特征不足或者现有特征与样本标签的相关性不强时，模型容易出现欠拟合。可以尝试添加更多的相关特征或使用特征工程技术来提取更有用的特征。
2. 增加模型复杂度：通过增加模型的复杂度来提高其拟合能力。例如，在神经网络模型中增加网络层数或神经元个数等。
3. 减小正则化系数：正则化是用来防止过拟合的，但当模型出现欠拟合现象时，则需要有针对性地减小正则化系数，以允许模型更灵活地拟合数据。

需要注意的是，在实际情况中，过拟合和欠拟合可能同时存在。因此，在选择模型和优化策略时，需要综合考虑偏差和方差之间的平衡，以及数据的特性。通过不断地调整模型复杂度、特征选择和训练策略，可以找到最适合当前任务的模型。