优质博文IT-BLOG-CN
一、题目
整数数组nums按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums在预先未知的某个下标k(0 <= k < nums.length)上进行了 旋转,使数组变为[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从0开始 计数)。例如,[0,1,2,4,5,6,7]在下标3处经旋转后可能变为[4,5,6,7,0,1,2]。
给你 旋转后 的数组nums和一个整数target,如果nums中存在这个目标值target,则返回它的下标,否则返回-1。
你必须设计一个时间复杂度为O(log n)的算法解决此问题。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
示例 3:
输入:nums = [1], target = 0
输出:-1
1 <= nums.length <= 5000
-104 <= nums[i] <= 104
nums中的每个值都 独一无二,题目数据保证nums在预先未知的某个下标上进行了旋转
-104 <= target <= 104
二、代码
将 「旋转数组查找目标值」 转化成 「有序数组查找目标值」
方案一:二分查找
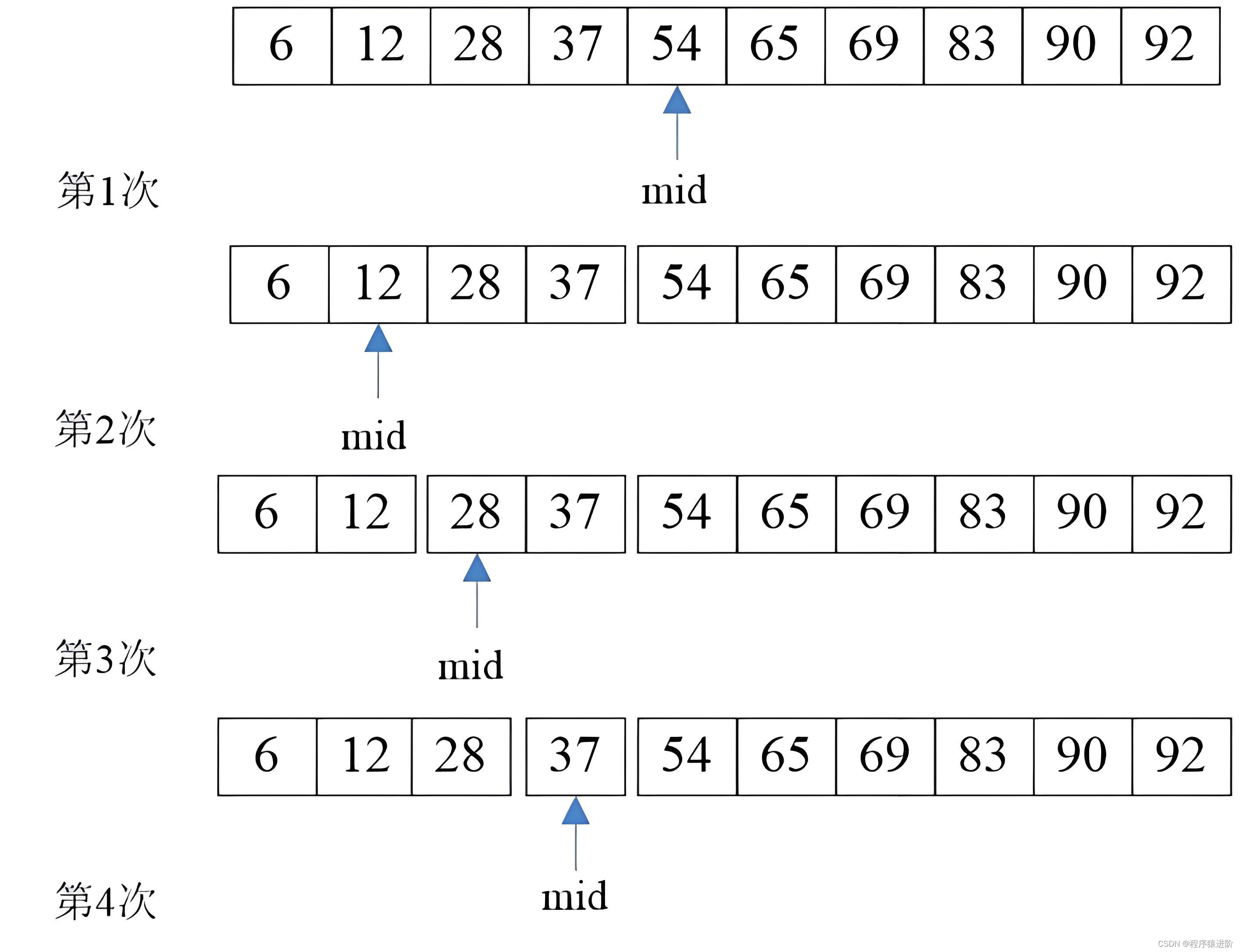
对于有序数组,可以使用二分查找的方法查找元素。
但是这道题中,数组本身不是有序的,进行旋转后只保证了数组的局部是有序的,这还能进行二分查找吗?答案是可以的。
可以发现的是,我们将数组从中间分开成左右两部分的时候,一定有一部分的数组是有序的。拿示例来看,我们从6这个位置分开以后数组变成了[4, 5, 6]和[7, 0, 1, 2]两个部分,其中左边[4, 5, 6]这个部分的数组是有序的,其他也是如此。
这启示我们可以在常规二分查找的时候查看当前mid为分割位置分割出来的两个部分[l, mid]和[mid + 1, r]哪个部分是有序的,并根据有序的那个部分确定我们该如何改变二分查找的上下界,因为我们能够根据有序的那部分判断出target在不在这个部分:
如果[l, mid - 1]是有序数组,且target的大小满足[nums[l],nums[mid]),则我们应该将搜索范围缩小至[l, mid - 1],否则在[mid + 1, r]中寻找。
如果[mid, r]是有序数组,且target的大小满足(nums[mid+1],nums[r]],则我们应该将搜索范围缩小至[mid + 1, r],否则在[l, mid - 1]中寻找。
需要注意的是,二分的写法有很多种,所以在判断target大小与有序部分的关系的时候可能会出现细节上的差别。
class Solution {
public int search(int[] nums, int target) {
int n = nums.length;
if (n == 0) {
return -1;
}
if (n == 1) {
return nums[0] == target ? 0 : -1;
}
int l = 0, r = n - 1;
while (l <= r) {
int mid = (l + r) / 2;
if (nums[mid] == target) {
return mid;
}
if (nums[0] <= nums[mid]) {
if (nums[0] <= target && target < nums[mid]) {
r = mid - 1;
} else {
l = mid + 1;
}
} else {
if (nums[mid] < target && target <= nums[n - 1]) {
l = mid + 1;
} else {
r = mid - 1;
}
}
}
return -1;
}
}
时间复杂度: O(logn),其中n为nums数组的大小。整个算法时间复杂度即为二分查找的时间复杂度O(logn)。
空间复杂度: O(1)。我们只需要常数级别的空间存放变量。
方案二:将旋转数组分成两段有序数组
可以将数组分为升序的两段,根据nums[0]与target的关系判断target在左段还是右段,再对升序数组进行二分查找即可。
对于旋转数组nums = [4,5,6,7,0,1,2]
首先根据nums[0]与target的关系判断target是在左段还是右段。
【1】例如target = 5, 目标值在左半段,因此在[4, 5, 6, 7, inf, inf, inf]这个有序数组里找就行了;
【2】例如target = 1, 目标值在右半段,因此在[-inf, -inf, -inf, -inf, 0, 1, 2]这个有序数组里找就行了。
如此,我们又双叒叕将「旋转数组中找目标值」 转化成了 「有序数组中找目标值」
class Solution {
public int search(int[] nums, int target) {
int lo = 0, hi = nums.length - 1;
while (lo <= hi) {
int mid = lo + (hi - lo) / 2;
if (nums[mid] == target) {
return mid;
}
// 先根据 nums[0] 与 target 的关系判断目标值是在左半段还是右半段
if (target >= nums[0]) {
// 目标值在左半段时,若 mid 在右半段,则将 mid 索引的值改成 inf
if (nums[mid] < nums[0]) {
nums[mid] = Integer.MAX_VALUE;
}
} else {
// 目标值在右半段时,若 mid 在左半段,则将 mid 索引的值改成 -inf
if (nums[mid] >= nums[0]) {
nums[mid] = Integer.MIN_VALUE;
}
}
if (nums[mid] < target) {
lo = mid + 1;
} else {
hi = mid - 1;
}
}
return -1;
}
}
方案三:调整左右边界 lo 和 hi
先根据nums[mid]与nums[lo]的关系判断mid是在左段还是右段,接下来再判断target是在mid的左边还是右边,从而来调整左右边界lo和 hi。
public int search(int[] nums, int target) {
int lo = 0, hi = nums.length - 1, mid = 0;
while (lo <= hi) {
mid = lo + (hi - lo) / 2;
if (nums[mid] == target) {
return mid;
}
// 先根据 nums[mid] 与 nums[lo] 的关系判断 mid 是在左段还是右段
if (nums[mid] >= nums[lo]) {
// 再判断 target 是在 mid 的左边还是右边,从而调整左右边界 lo 和 hi
if (target >= nums[lo] && target < nums[mid]) {
hi = mid - 1;
} else {
lo = mid + 1;
}
} else {
if (target > nums[mid] && target <= nums[hi]) {
lo = mid + 1;
} else {
hi = mid - 1;
}
}
}
return -1;
}
方案四:快排思路的延申
int search(int* nums, int numsSize, int target){
int i;
if(numsSize==0)
{
return -1;
}
for(i=0;i<numsSize/2+1;i++)
{
if(nums[i]==target)
{
return i;
}
else if(nums[numsSize-i-1]==target)
{
return numsSize-i-1;
}
else
{
continue;
}
}
return -1;
}