【LeetCode】升级打怪之路 Day 12：单调队列

news2024/11/15 13:23:05

今日题目：

239. 滑动窗口最大值 | LeetCode

今天学习了单调队列这种特殊的数据结构，思路很新颖，值得学习。

Problem：单调队列【必会】

与单调栈类似，单调队列也是一种特殊的数据结构，它相比与普通的 queue，增加了一个新的接口 max() 来获取当前队列的最大值。

新增的 max() 是我们选用这个数据结构的最重要原因，单调队列不仅仅可以通过 offer() 和 poll() 接口来实现 FIFO 的元素进出顺序，还额外增加了 max() 接口让我们获取到当前队列中的最大元素。

单调队列主要用来解决下面这个场景：我们会时刻向一个集合中增加新元素或减少旧元素，同时每次可以获取到当前这个集合中的最大值。优先级队列也可以满足这个需求，但优先级队列无法满足 FIFO 的元素进出顺序，这也是必须使用单调队列的原因。

假如有一个数组 window，并知道它的最大值是 A，此时向 window 增加一个新元素 B，我们只需要比较 A 和 B 就可以得到当前 window 中的最大值；但如果删除一个旧元素 C，就麻烦了，因为如果这个删除的 C 恰恰就是最大值 A，那么最大值就要重新遍历 window 来寻找了，从而导致复杂度飙升。这就是单调队列所需要解决的难题。

下面看一下单调队列的经典应用：滑动窗口最大值。

LC 239. 滑动窗口最大值【classic】 ⭐⭐⭐⭐⭐

239. 滑动窗口最大值 | LeetCode

如果我们能够实现数据结构“单调队列” MonoQueue，那我们就每次向右滑动我们的窗口时，向 monoQueue 中新增一个窗口右边的新元素，移除一个窗口左边的旧元素，然后调用 max() 接口获取当前窗口的最大值，就可以计算出题目所需要的最终结果。

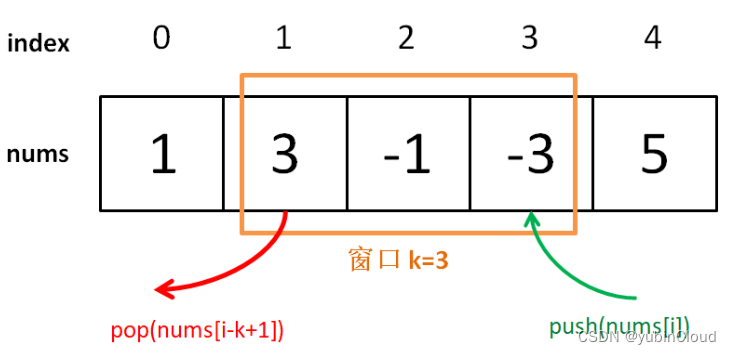
在这里插入图片描述

所以重点在于如何实现 MonoQueue。

我们需求的关键是：需要能够快速得知当前队列中的最大值。由于窗口滑动时是有顺序的，先进入的元素一定会先出去，所以如果新进入的一个元素，那么比它老的还比它小的那些元素就永远不可能成为当前队列中的最大值了，因为老元素一定会比新元素更早地离开队列。所以，每次在入队一个新元素时，就可以把队列中比他小的元素都抛弃掉了：

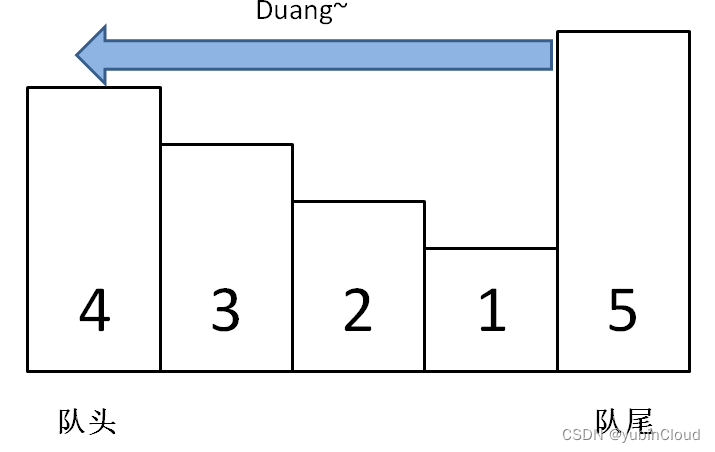
在这里插入图片描述
如上图，当元素 5 进入队列后，就可以一下子把 4、3、2、1 全给抛弃掉了，因为这些旧元素在队列的时候 5 一定在，所以这些旧元素一定成不了“当前队列的最大值”。

根据以上分析，单调队列 MonoQueue 的实现如下：

class MonoQueue {
    private Deque<Integer> maxQ = new LinkedList<>();
    
    public void offer(int num) {
        // 将小于 num 的元素全部删除
        while (!maxQ.isEmpty() && maxQ.getLast() < num) {
            maxQ.removeLast();
        }
        // 将 num 加入队尾
        maxQ.addLast(num);
    }

    public int max() {
        return maxQ.getFirst();  // 单调队列，队首就是最大元素
    }

    public void poll(int n) {
        if (maxQ.getFirst() == n) {  // 判断需要移除的是否是队首，如果不是的话，就是比队首小还比队首老的元素，已经被移除了，那就啥也不用干
            maxQ.removeFirst();
        }
    }
}

这里有两个易错点：

在 offer() 函数实现中，第一步删掉掉小于 num 的元素，但注意别把等于它的元素删除了，因为如果把相等的元素也删掉的话，实现 poll() 接口时，就不太好判断队首最大元素是否就是我们当前需要 poll 的元素了（我们是通过值相等来判断的）
在实现 poll() 函数时，其参数 n 表示期待删除的元素，因为我们这个 MonoQueue 并没有保留全部入队元素，所以当需要删除一个已经被删除的元素时，poll() 接口只需要立刻返回就可以了。

在实现了 MonoQueue 后，我们解决这个问题就容易多了：

    public int[] maxSlidingWindow(int[] nums, int k) {

        MonoQueue monoQueue = new MonoQueue();
        List<Integer> result = new ArrayList<>();

        // 将前 k-1 个元素填充到队列中
        for (int i = 0; i < k - 1; i++) {
            monoQueue.offer(nums[i]);
        }

        for (int i = k - 1; i < nums.length; i++) {
            // 加入窗口右边的新元素
            monoQueue.offer(nums[i]);
            // 获取窗口内最大元素，并加入到结果集中
            result.add(monoQueue.max());
            // 移除窗口左边的旧元素
            monoQueue.poll(nums[i - k + 1]);
        }

        return result.stream().mapToInt(Integer::valueOf).toArray();
    }