函数式编程

在编程范式中有很多分类，面向对象式，命令式编程，声明式编程等，而函数式编程也是一种重要的编程范式。

函数式编程（Functional Programming)，FP是一种将计算视为函数求值过程的编程范式，并强调使用纯函数、不可变数据和函数组合来构建软件系统。函数式编程强调将程序分解成若干独立的函数，并通过函数之间的组合和组合操作来解决问题。
特点：

1. 纯函数：函数式编程强调使用纯函数，即没有副作用、只依赖于输入参数并返回结果的函数。
2. 不可变数据：函数式编程鼓励使用不可变数据，避免修改已有数据，而是通过创建新的数据来实>现状态的改变。
3. 函数组合：函数式编程支持函数的组合，可以将多个函数组合成一个更复杂的函数，提高代码的复用性和可读性。
4. 延迟计算：函数式编程中的操作通常是延迟计算的，只有在需要结果时才会进行计算，这提供了>更高的灵活性和效率。

为什么使用函数式编程

请看以下两端功能相同的代码：

程序要求：
1.写一个程序，输入一个n(n>=0)，判断n是否为素数
2.若为素数则输出一2 * n， 若不是素数则输出n / 2

#include<stdio.h>

int isprime(int n){
    for(int i = 2; i <= (n >> 1); i++){
        if(!(n % i)) return 0;
    }
    return 1;
}

int func(int n){
    if (isprime(n)){
        return n * 2;
    }
    else return n / 2;
}

int main(){
    int n;
    while(~scanf("%d", &n)){
        if(isprime(n)){
            printf("%d is prime!\n", n);
        }
        else{
            printf("%d is not prime\n", n);
        }
        printf("And output a %d\n", func(n));
    }

}

/*************************************************************************
        > File Name:1-example-about-why-use-function.c
        > Author:
        > Mail:
        > Created Time: Sun 03 Mar 2024 01:16:24 PM CST
    	> content: input a number "n"(n > 0), and output the prime of the range from 1 to the number.
 ************************************************************************/

#include<stdio.h>
int main(){
    int n, flag;
    while(~scanf("%d", &n)){
        flag = 1;
        for(int i = 2 ; i < (n >> 1); i++){
            if(!(n % i)) flag = 0;
        }

        if (flag){
            printf("%d is prime!\n", n);
            printf("And output a %d\n", n * 2);

        }
        else{
            printf("%d is not prime\n", n);
            printf("And output a %d\n", n / 2);
        }
    }

从两段代码不难看出过程式的编程更加繁重，且可扩展性很差，若是在添加一个新功能，函数式编程可以通过再加一个函数来实现，主函数的总体框架不会变，但是若是以第二种方式的话，很有可能需要产生大的变动，而且从阅读上来讲，函数式的编程所呈现的更加直观，不需要关心怎么实现的上一步，若想要知道具体的实现方法，也只需查看相关的功能函数即可，对于debug来讲也就更方便。

函数说明

# 函数的结构
int isprime(int n){   #int 为返回值  #isprime为函数名  #int n 参数声明列表(其中int 是限制传输参数的限制类型)
    for(int i = 2; i <= (n >> 1); i++){
        if(!(n % i)) return 0;
    }
    return 1;
}

函数分为两个部分：1. 函数声明 2. 函数定义
上面展示的就是函数定义的部分，函数的声明和变量声明相同，在使用之前需要先声明，告诉编译器变量的存在，因为C语言是顺序执行的，若是函数在使用之前，就先定义了，那么编译器就已经知道了该函数的存在，所以就不需要声明了，反之则需要声明。

# 需要声明的情况
#include<stdio.h>
int funb();
int funa(int x){
	return funb(x);
}
int funb(int x){
	return x;
}

K&R风格定义

int isprime(x)
int x;
{
    for (int i = 2; i * i <= x; i++){
        if(!(x % i)) return 0;
    }
    return 1;
}

不建议使用这种方式，这是一种已经过时的函数定义风格，但是现在的编译器依然可以编译通过，但是只做了解，极其不建议使用。

递归

在使用函数时，个人认为最重要的就是理解递归这种编程方法的使用，理解递归思维。

递归实际上就是程序调用自身的编程技巧
递归程序的组成：

1. 边界条件处理
2. 针对于问题的处理过程和递归过程
3. 结果返回

以实际问题为例，写一个程序实现输入一个大于0的数字n，输出n(n < 30)的阶乘

/*************************************************************************
        > File Name: 3-factorial.c
        > Author:
        > Mail:
        > Created Time: Sun 03 Mar 2024 02:28:28 PM CST
 ************************************************************************/

#include<stdio.h>

int factorial(int n){
    if(n == 1 || n == 0) return 1;
    return n * factorial(n - 1);
}

int main(){
    int n;
    while(~scanf("%d", &n)){
        printf("%d! = %d\n", n, factorial(n));
    }
}

实现思路：
0！和1！等于1，这个条件可以作为出口，除此之外可知计算阶乘$n!=n\ast (n-1)!$，这个就是函数的处理过程。

递归：1. 向上递推 2. 向下回归(回溯)
$$fac(5)=5\ast fac(4)=5\ast (4\ast fac(3))=5\ast (4\ast (3\ast fac(2)))=5\ast (4\ast (3\ast (2\ast fac(1))))=5\ast (4\ast (3\ast (2\ast (1))))$$
运算过程由内括号向外运算，即是递归的运算过程，就像是小时候传纸条一样，依次传到你的目标人物，停止传递，而后纸条传回来的一个过程。

如何判断递归过程是正确的：数学归纳法
$$\begin{gathered} f(1)=1 \\ f(2)=f(1)\ast 2=1\ast 2 \\ f(3)=f(2)\ast 3=f(1)\ast 2\ast 3=1\ast 2\ast 3 \\ ... \\ ... \\ f(k)=f(k-1)\ast k=...=1\ast 2\ast ...\ast (k-1)\ast k \end{gathered}$$

系统栈

在递归过程中，函数进行自我调用时，需要借助的系统栈。根据以上的演示可知，递归实际上是层层调用自己的过程，而对于函数的执行顺序，却是反过来的，求解f(5)的过程是$$f(5)->f(4)->f(3)->f(2)->f(1)$$只有当运行到f(1)的时候，触发了出口条件，得到f（1）的值，返回到f(2)进而依次到f(5)得出结果。也就是说最后调用的是f(1)，最先运算的也是f(1)也就是后进先出，在这个递推过程中，未进行运算的函数则存放在栈中，等待进行运算。在windows系统中系统栈的大小为2MB，Linux系统中为8MB(我所进行代码演示的系统)。而每层压入栈中的数据大小为一个函数指针8bytes(64bit 操作系统) + 一个整型变量4bytes = 12bytes（以演示的阶乘程序为例）。随着变量的的增多压入栈中的大小也会变化，所以当压入栈中的数据大小超过栈大小时，就会爆栈(栈溢出)

函数指针

函数指针实际上就是一个地址，及变量，所以可以当作参数传入函数，即可以把函数当作函数。

/*************************************************************************
        > File Name: 4-fun-address.c
        > Author:
        > Mail:
        > Created Time: Sun 03 Mar 2024 08:16:28 PM CST
 ************************************************************************/

#include<stdio.h>

int add(int a, int b){
    return a + b;
}

int substract(int a, int b){
    return a - b;
}

int calculate(int (*f1)(int, int), int (*f2)(int, int), int a, int b){
    if(a > b){
        return f1(a, b);
    }
    else if(a < b){
        return f2(a, b);
    }
    return a;
}
int main(){
    int a, b;
    while(~scanf("%d%d", &a, &b)){
        printf("the result :%d\n", calculate(substract,add,a, b));
    }
}

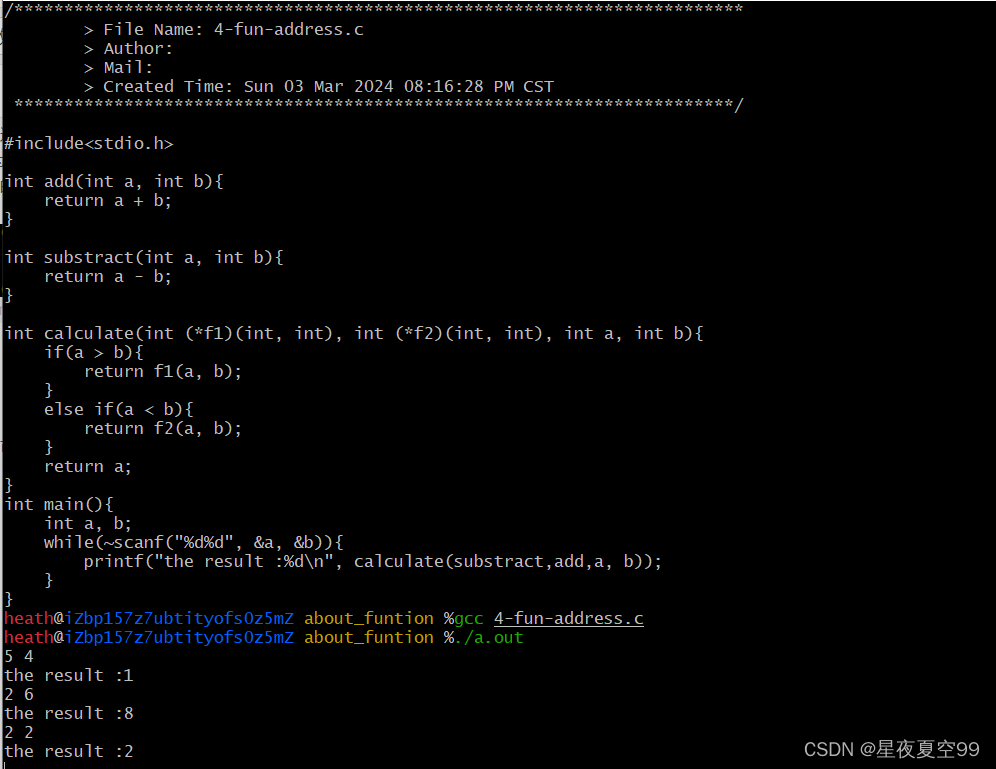
上面我们说过，函数运行呢是把函数指针以及参数压入到系统栈中，运行时弹栈，也就说，函数的运行实际上是通过指针找到所在地址来运行，指针变量也是变量，所以我们同样可以作为参数传入到函数当中。我们通过函数传参的方式可以则可以轻易的实现出分段函数。