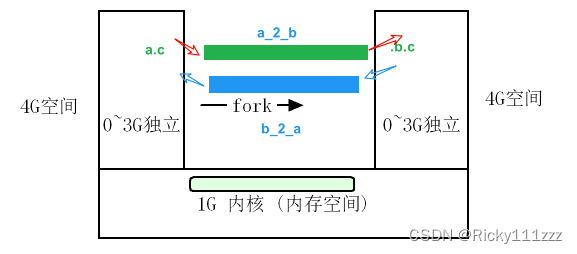
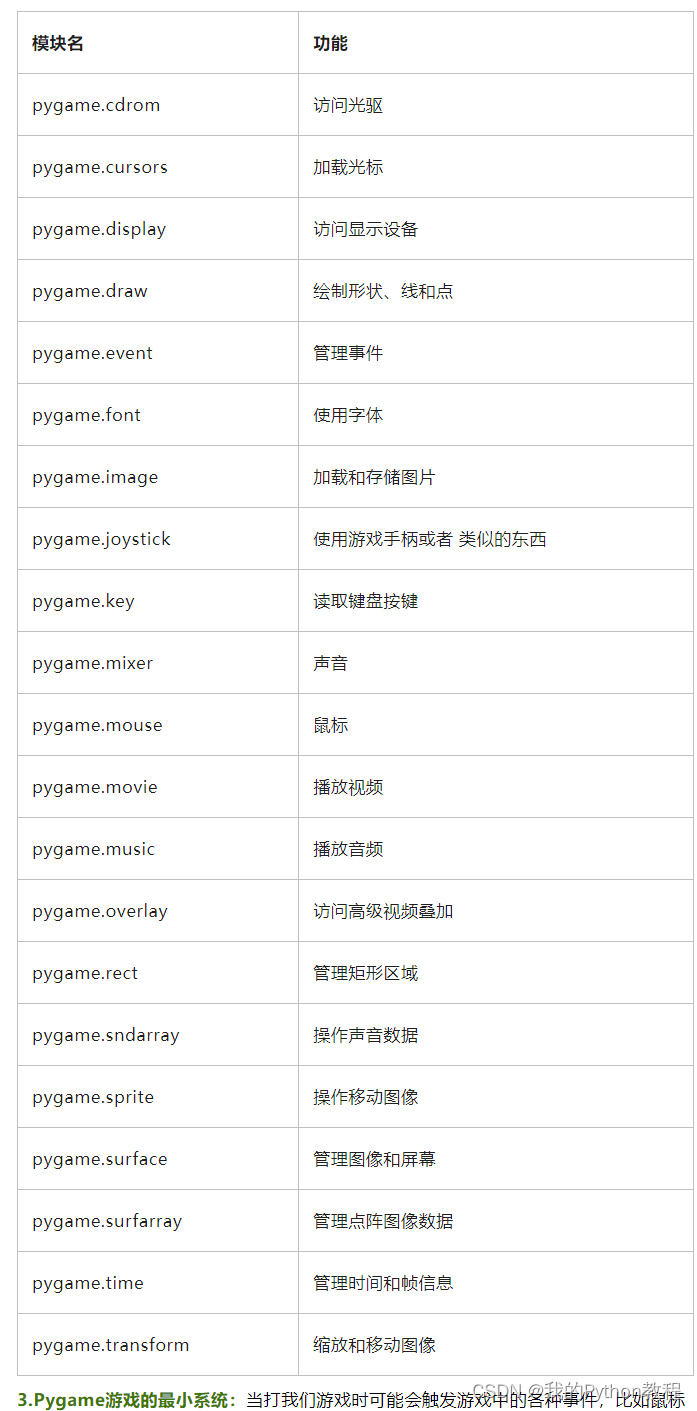
文章目录
- 题目描述
- 代码
题目描述
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 1:
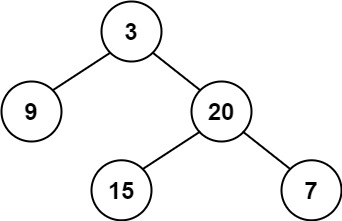
输入:root = [3,9,20,null,null,15,7]
输出:true
示例 2:
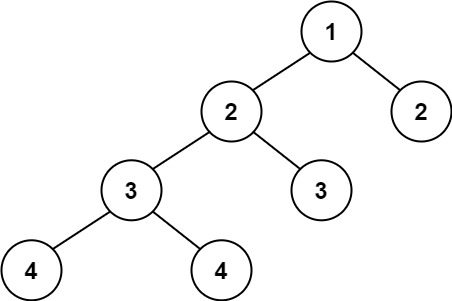
输入:root = [1,2,2,3,3,null,null,4,4]
输出:false
示例 3:
输入:root = []
输出:true
提示:
树中的节点数在范围 [0, 5000] 内
-104 <= Node.val <= 104
代码
使用递归的方式比较好解决。在求当前节点的高度的时候就能知道孩子节点的高度,如果孩子节点的高度不满足平衡二叉树的定义就立刻返回-1。
如果发现孩子节点的高度已经是-1了则证明子树中某个节点肯定是不满足平衡二叉树了,所以可以直接返回-1。
class Solution {
public boolean isBalanced(TreeNode root) {
//使用递归的方式比较好解决
//如果root返回-1,则表示root或其孩子节点中有不满足平衡二叉树定义的
if (getHeight(root)==-1){
return false;
}
return true;
}
//用来递归
public int getHeight(TreeNode root){
if (root==null){
return 0;
}
int leftHeight = getHeight(root.left);
int rightHeight = getHeight(root.right);
//当有一个节点不满足平衡二叉树的定义的时候就返回-1,所以如果下面的节点返回了-1就直接返回-1
if (leftHeight==-1){
return -1;
}
if (rightHeight==-1){
return -1;
}
//比较当前节点的左右孩子高度差
if (Math.abs(leftHeight-rightHeight)>1){
return -1;
}
//返回当前节点的高度,也就是左右子树中最大的高度加一
return Math.max(leftHeight,rightHeight)+1;
}
}




![[C++]AVL树怎么转](https://img-blog.csdnimg.cn/direct/1dc15693bc134af68195cfa67540e4c3.png#pic_center)