图像压缩
曾经看到过,这是一道洛谷原题,很可惜我没做过,有点看不懂就没尝试。
原题链接:B3851 [GESP202306 四级] 图像压缩 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
因数分解

直接枚举就行了,从2开始找因子,到sqrt(n),从小到大能被除的话一定是素数。
假设a<b<c,且a和c是素数因子,b是合数因子。
由于合数可以由素数因子相乘得到:那么b=d+e,且d和e均小于等于sqrt(b),故从2到sqrt(n)遍历能除的除干净之后,除出来的必然是素数。
对于大于sqrt(n)部分的因子,合数因子必然能分解成小于sqrt(n)的部分,除完之后还有剩下的,那么剩下的就为素数。
Q:有没有可能剩下的素数有两个。
A:两个素数均大于sqrt(n),则乘积大于n,不合法。故最多一个。
最后考虑特殊情况,如果上面循环完了n还不为1,那么n就是素数。
#include <bits/stdc++.h>
#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define debug(a) cout<<#a<<"="<<a<<endl
#define fr first
#define se second
#define endl '\n'
using namespace std;
void solve(){
int n;
cin>>n;
map<int,int>f;
int a=n;
per(i,2,sqrt(n)){
if(a%i==0){
int cnt=0;
while(a%i==0){
a/=i;
cnt++;
}
f[i]=cnt;
}
}
if(a>1)f[a]++;
auto it=f.rbegin();
for(auto i:f){
if(i.se==1){
cout<<i.fr<<" ";
}else{
cout<<i.fr<<"^"<<i.se<<" ";
}
if(i!=*it){
cout<<"* ";
}
}
}
signed main(){
ios::sync_with_stdio(false),cin.tie(nullptr);
int t=1;
while(t--)solve();
return 0;
}一个数可以分解数质数相乘。
更细化的,这些质数可以是偶数个或者奇数个。如 2 * 3 都只有一个,而 2^2*3,2有两个。
所以我们可以把质数分成 数量为奇数的 和 数量为偶数的。
根据从小到大能除除干净,除出来的是质数,我们可以先分离出数量为偶数的。
per(i,2,sqrt(n)){
int x=i*i;
while(n%x==0)f[i]+=2,n/=x;
}假设一个平方质因子都没分离出来,那么n=a*b*c*d a,b,c,d为素数且均为一个。
所以只需要2~sqrt(n)遍历一次,大于sqrt(n)的只有一个,故如果n除完之后大于1,这就是那一个大于sqrt的数。
总复杂度sqrt(n)+sqrt(n),但是这样可以分离出所有的单个因子,有需要的话可以提供更多思路。
#include <bits/stdc++.h>
#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define debug(a) cout<<#a<<"="<<a<<endl
#define fr first
#define se second
#define endl '\n'
using namespace std;
void solve(){
int n;
cin>>n;
map<int,int>f;
per(i,2,sqrt(n)){
int x=i*i;
while(n%x==0)f[i]+=2,n/=x;
}
per(i,2,sqrt(n)){
if(n%i==0){
f[i]++;
n/=i;
}
}
if(n>1)f[n]++;
auto it=f.rbegin();
for(auto i:f){
if(i.se>=2){
cout<<i.fr<<"^"<<i.se<<" ";
}else cout<<i.fr<<" ";
if(i!=*it){
cout<<"* ";
}
}
}
signed main(){
ios::sync_with_stdio(false),cin.tie(nullptr);
int t=1;
while(t--)solve();
return 0;
}探险
这道题应该才是签到题。不过被榜单带歪了都是先做的 因数分解 和 求和。

可以肯定的是,小理一定在某个洞穴停下,剩下的次数全部用来反复进入前面进入过的洞穴,且反复进入的洞穴一定是同一个,经验值最大的那一个。
那么只需要枚举所有情况就可以了。
#include <bits/stdc++.h>
#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define debug(a) cout<<#a<<"="<<a<<endl
#define fr first
#define se second
#define endl '\n'
using namespace std;
void solve(){
int n,k;
cin>>n>>k;
vector<int> a(n+1),b(n+1);
per(i,1,n)cin>>a[i];
per(i,1,n)cin>>b[i];
int f=0,res=0,ans=0;
per(i,1,min(n,k)){
int leave=k-i;//剩下的次数
f+=a[i];//开洞穴累计的经验值
res=max(res,b[i]);//前面开过的洞穴最大的那一个
ans=max(ans,leave*res+f);//累计答案
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(false),cin.tie(nullptr);
int t=1;
cin>>t;
while(t--)solve();
return 0;
}最小乘积
这道题显然官方数据集弄错了,导致一个人都没有通过。

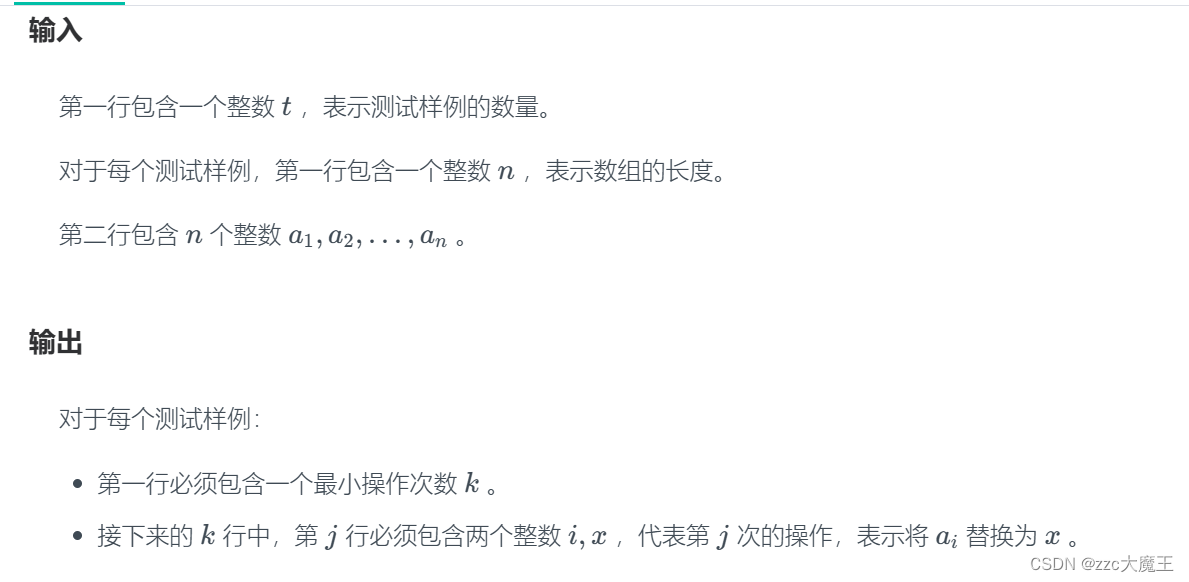
可以进行的操作:
1、ai<0 可以将 ai 替换成 [ai,0] 其中的一个。
2、ai>=0 可以将 ai 替换成 [0,ai] 其中的一个。(显然 0 不能做修改)
要求进行最少的操作,使得数组的乘积最小。
只需要记录一下正数,负数,0,的数量即可。
如果存在 0,显然不管怎么操作最后乘积都是0,则不需要操作。
如果不存在 0,若 负数 有奇数个,那么最终乘积为负数,不需要修改。
若 负数 有偶数个,那么乘积一定正数,任意一个改成0。
无人AC。
#include <bits/stdc++.h>
#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define debug(a) cout<<#a<<"="<<a<<endl
#define fr first
#define se second
#define endl '\n'
using namespace std;
void solve(){
int n;
cin>>n;
int pos=0,neg=0,zero=0;
per(i,1,n){
int tmp;
cin>>tmp;
if(tmp>0)pos++;
else if(tmp<0)neg++;
else if(tmp==0)zero++;
}
if(zero){
cout<<0<<endl;
}else{
if(neg%2==0){
cout<<1<<endl;
cout<<1<<" "<<0<<endl;
}else{
cout<<0<<endl;
}
}
}
signed main(){
ios::sync_with_stdio(false),cin.tie(nullptr);
int t=1;
cin>>t;
while(t--)solve();
return 0;
}若此非正解请在评论区留言,否则建议大伙避雷该比赛,且本次全国赛算法科目只有120个左右参加,好少的人。
求和
一道哈人的模拟题。


思路比较简单,就是数字全部提取出来加在一起。
需要注意的是负号-,有可能作为分隔符使用。
如2-3,输出的是2+3=5
而2--3,输出的是2-3=-1
那么作为分割符的条件就很明显了,前面不能是数字。
由于输入没有告知多少行,且中间可能存在空行,所以我们使用getline来读入。
string s;
while(getline(cin,s))本地调试的时候如果没有结果,请按下Ctrl+D,相当于输入文件末尾的EOF。
#include <bits/stdc++.h>
//#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define debug(a) cout<<#a<<"="<<a<<endl
#define fr first
#define se second
#define endl '\n'
using namespace std;
void solve(){
string s;
while(getline(cin,s)){
int res=0,ans=0;
bool havNum=false;
int pos=1;//是否是正数
if(s.empty())continue;//什么都没有输入直接跳过
per(i,0,s.length()-1){
if(s[i]>='0' and s[i]<='9'){
havNum=true;
res*=10;
res+=s[i]-'0';
}else if(s[i]=='-' and s[i+1]>='0' and s[i+1]<='9' and !(s[i-1]>='0' and s[i-1]<='9')){
pos=-1;
}else{
// debug(res*pos);
ans+=res*pos;
pos=true;
res=0;
}
}
if(res)ans+=res*pos;//考虑最后结尾是数字,没有累加上的情况。
if(havNum)cout<<ans<<endl;//字符串中至少有一个整数才能输出。
}
}
signed main(){
ios::sync_with_stdio(false),cin.tie(nullptr);
int t=1;
while(t--)solve();
return 0;
}