文章目录
- [2859. 计算 K 置位下标对应元素的和](https://leetcode.cn/problems/sum-of-values-at-indices-with-k-set-bits/)
- 思路:
- [938. 二叉搜索树的范围和](https://leetcode.cn/problems/range-sum-of-bst/)
- 思路:
- 写法一:在中间累加
- 写法二:在最后累加
- 1028. 从先序遍历还原二叉树(三种方法:栈+递归+集合)
- 一、栈+ while迭代
- 1.思路
- 2.代码
- 二、递归法
- 1.思路
- 2.代码
- 三、集合存储
- 1.思路
- 2.代码
2859. 计算 K 置位下标对应元素的和

思路:
遍历输入列表,对于满足特定条件的元素做一些操作并将结果累加起来。其中,bitCount 辅助方法用于计算一个整数的二进制表示中有多少个 1。
- 遍历给定列表
nums中的所有元素,用索引i表示当前元素所在位置。 - 对于每个索引
i,调用辅助方法bitCount(i),返回它的二进制表示中 1 的个数。 - 检查步骤 2 中得到的 1 的个数是否等于给定值
k。 - 如果匹配,则将当前索引
i所在位置上的值加入到答案ans中。 - 循环结束后,返回
ans作为最终结果。
public int sumIndicesWithKSetBits(List<Integer> nums, int k) {
int ans = 0;
for (int i = 0; i < nums.size(); ++i) {
if (bitCount(i) == k) {
ans += nums.get(i);
}
}
return ans;
}
/**
* 计算一个整数的二进制表示中有多少个1
* @param x 要计算的整数
* @return 二进制中1的个数
*/
public int bitCount(int x) {
int cnt = 0;
while (x != 0) {
cnt += (x % 2);
x /= 2;
}
return cnt;
}
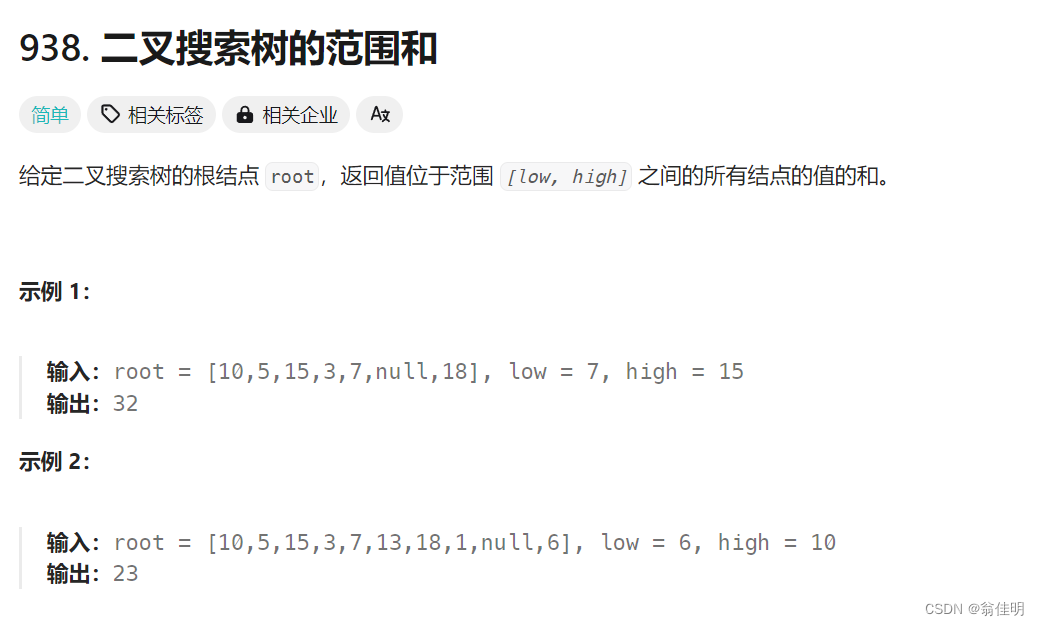
938. 二叉搜索树的范围和
思路:
1.在二叉搜索树中:左子树的结点都小于根节点,右子树的结点都大于根节点,每个结点法左右子树均要符合二叉搜索树
2.如果根节点的值大于hight,就排除右树,只在左树中查找
3.如果根节点的值小于low,就排除左树,只在右树中查找
4.如果正好在两者之间,则左树右树都要考虑,将根节点的值和递归的结果累加
写法一:在中间累加
//[938. 二叉搜索树的范围和]-写法二
//
public int rangeSumBST2(TreeNode root, int low, int high) {
if (root==null){
return 0;
}
int x = root.val;
int sum = low<=x && x<=high?x:0;
//根节点的值如果在范围内,返回根节点的值,否则就返回0,相当于排除了不在范围内的值
if(x>low){
sum+=rangeSumBST2(root.left,low,high);
}
if (x<high){
sum+=rangeSumBST2(root.right,low,high);
}
return sum;
}
写法二:在最后累加
//[938. 二叉搜索树的范围和]
public int rangeSumBST(TreeNode root, int low, int high) {
if (root == null) {
return 0;
}
int x = root.val;
if (x > high) {
return rangeSumBST(root.left, low, high);
//右树不在范围内,只需要递归左树
}
if (x < low) {
return rangeSumBST(root.right, low, high);
//左树不在范围内,只需要递归左树
}
return x + rangeSumBST(root.left, low, high) + rangeSumBST(root.right, low, high);
//左右子树都可能
}
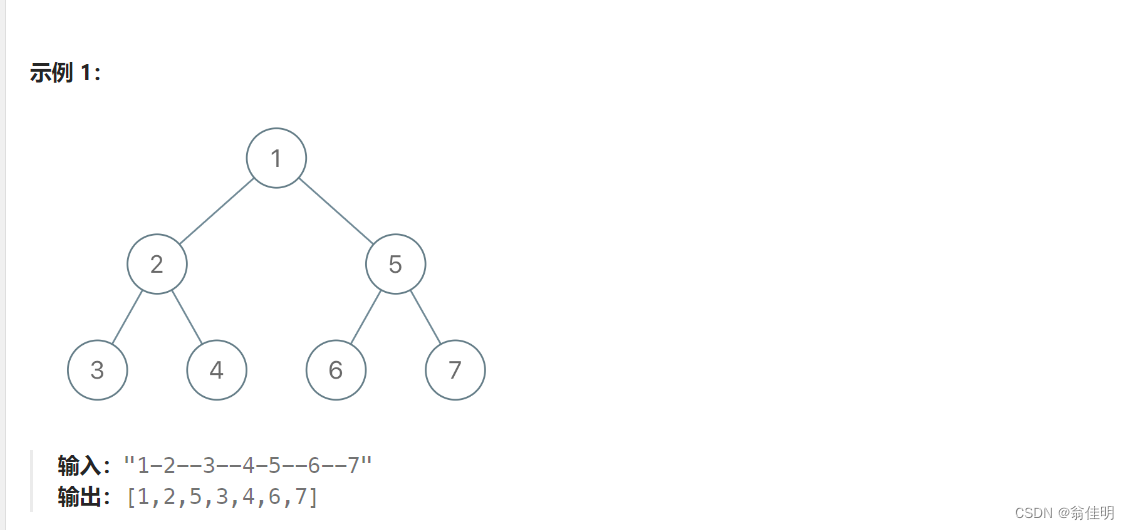
1028. 从先序遍历还原二叉树(三种方法:栈+递归+集合)

一、栈+ while迭代
1.思路
1.遍历整个字符串,从0开始,根节点在第0层
2.用level记录层数,每遇到一个-字符,当前层数+1
3.用val记录要插入的结点的值,遍历取到的数字,通过字符运算得到值。
4.找到当前要插入结点的父结点,栈的大小要小于当前层数
5.如果节点只有一个子节点,那么保证该子节点为左子节点。
6.将创建的新结点入栈
7.除了根节点,其他子节点全部出栈,返回根节点
2.代码
public TreeNode recoverFromPreorder(String traversal) {
Stack<TreeNode> stack = new Stack<>();
//用栈来存储结点
for (int i = 0; i < traversal.length(); ) {
//遍历整个字符串,从0开始,根节点在第0层
int level = 0;
//记录当前层数
while (traversal.charAt(i) == '-') {
//每遍历到一个-,层数累加
level++;
i++;
}
int val = 0;//查看当前要插入结点的数字
while (i < traversal.length() && traversal.charAt(i) != '-') {
//当前的字符是数字,并且未超过字符串
val = val * 10 + (traversal.charAt(i) - '0');
//根据字符的相加,遍历字符串找数字时 只能一个数字一个数字的转,
// 但是字符串中连续的数字是一个多位数,需要前面的数字*10变高位,再加上后面的数,
// 成为一个数,作为新结点的值
i++;
}
while (stack.size() > level) {
stack.pop();
//找到当前要插入结点的父结点
}
TreeNode node = new TreeNode(val);//创建新结点
if (!stack.isEmpty()) {
//如果节点只有一个子节点,那么保证该子节点为左子节点。
if (stack.peek().left == null) {
stack.peek().left = node;
} else {
stack.peek().right = node;
}
}
stack.add(node);//入栈
}
while (stack.size() > 1) {
stack.pop();
//要返回根节点,出到栈只有一个结点
}
return stack.pop();
}
二、递归法
1.思路
1.利用helper函数,根据字符和对应深度创建结点,还原二叉树
2.每遇到-字符,层数加一
3.如果遍历的深度和获取到的深度不一致,返回空
4.当深度等于层数时,下一个结点的位置从index + level开始
5.通过字符运算获取数字,同时创建结点
6.根节点的左树调用helper函数递归,如果左子节点是空,那么右子节点肯定也是空的
7.如果根节点的左树不为空,要想添加结点,递归右树。
8.最终返回根节点
2.代码
//102. 二叉树的层序遍历---递归写法
int index = 0;
//index记录遍历到字符串的哪个位置
public TreeNode recoverFromPreorder3(String traversal) {
return helper(traversal,0);
}
public TreeNode helper(String s, int depth) {
//helper函数用来创建二叉树
int level = 0;
//记录层数
while (index + level < s.length() && s.charAt(index + level) == '-') {
level++;
}
//如果遍历的深度和获取到的深度不一致,返回空
if (level != depth){
return null;
}
int next = index + level;
//获取数字
while (next < s.length() && s.charAt(next) != '-')
next++;
int val = Integer.parseInt(s.substring(index + level, next));
index = next;
//创建结点
TreeNode root = new TreeNode(val);
root.left = helper(s, depth + 1);
if (root.left == null) {//如果左子节点是空,那么右子节点肯定也是空的
root.right = null;
} else {
root.right = helper(s, depth + 1);
}
return root;
}
三、集合存储
1.思路
1.使用正则匹配把字符串S拆成不同的数字存进数组中,用集合list来存储结点
2.将根节点添加到list中,层数从1开始,不包括根节点
3.数组存储的位置不为空时,根据转换的值创建结点
4.将结点加入到集合中
5.获取父结点,插入结点,并从新设置层数,果满了,层数加一
6.最终返回根节点
2.代码
//102. 二叉树的层序遍历--正则匹配
public TreeNode recoverFromPreorder2(String traversal) {
String[] valus = traversal.split("-");
//使用正则匹配把字符串S拆成不同的数字,用集合list来存储结点
List<TreeNode> list = new ArrayList<>();
list.add(new TreeNode(Integer.valueOf(valus[0])));//根节点
//根节点添加到list中
int level = 1;//层数层1开始,不包括根节点
for (int i = 1; i < valus.length; i++) {
if (!valus[i].isEmpty()) {
//数组存储的位置不为空
TreeNode node = new TreeNode(Integer.valueOf(valus[i]));
//根据转化的值,创建结点
//因为是前序遍历,每层我们只需要存储一个结点即可,这个节点值有可能
//会被覆盖,如果被覆盖了说明这个节点以及他的子节点都以及遍历过了,
//所以不用考虑被覆盖问题
list.add(level, node);
//将结点加入到集合中
TreeNode parent = list.get(level - 1);
//获取父结点,插入结点,并从新设置层数
if (parent.left == null) {
parent.left = node;
} else {
parent.right = node;
}
level = 1;
} else {
level++;
//如果满了,层数加一
}
}
return list.get(0);
}
点击移步博客主页,欢迎光临~