应用机器学习回归离群值处理

news2024/9/28 23:22:44

异常值可能会破坏机器学习模型的运转，导致结果出现偏差并影响准确性。在这篇博文中，我们将深入研究应用机器学习领域，并探索使用 Python 识别和处理异常值的有效技

了解异常值

离群值是与数据集其余部分显着偏差的数据点。它们可能是错误、异常或仅仅是极端值的结果。解决异常值对于确保机器学习模型的稳健性至关重要。

可视化检测：

首先使用箱线图、散点图或直方图直观地检查数据。通常可以通过肉眼检测到与标准的严重偏差。

统计方法：

使用 Z 分数或 IQR（四分位距）等统计方法来量化与平均值或中位数的偏差程度。

import numpy as np
from scipy import stats

def detect_outliers_zscore(data, threshold=3):
    z_scores = np.abs(stats.zscore(data))
    return np.where(z_scores > threshold)

def detect_outliers_iqr(data):
    q1, q3 = np.percentile(data, [25, 75])
    iqr = q3 - q1
    lower_bound = q1 - 1.5 * iqr
    upper_bound = q3 + 1.5 * iqr
    return np.where((data < lower_bound) | (data > upper_bound))

异常值处理：

插补：

将离群值替换为平均值、中位数或自定义插补方法。

def impute_outliers(data, method='median'): data , method= 'median' ): 
    if method == 'mean' : 
        replacement_value = np.mean( data ) 
    elif method == 'median' : 
        replacement_value = np.median ( data ) 
    else : 
        # 自定义插补方法
        replacement_value = custom_imputation( data ) 
    
    outliers = detector_outliers_iqr( data ) 
    data [outliers] = replacement_value 
    return  data

截断：

将极值限制在指定范围内。

def truncate_outliers(data, lower_bound, upper_bound):data, lower_bound, upper_bound):
    outliers = detect_outliers_iqr(data)
    data[outliers] = np.clip(data[outliers], lower_bound, upper_bound)
    return data

实例：预测房价

让我们将这些异常值处理技术应用于房价数据集。我们将加载数据，识别异常值，并采用插补和截断方法。

# Identify outliers using IQR
outliers = detect_outliers_iqr(data['price'])

# Impute outliers with median
data['price'] = impute_outliers(data['price'], method='median')

# Truncate outliers to a specified range
data['price'] = truncate_outliers(data['price'], lower_bound=10000, upper_bound=500000)

让我们考虑一个使用学生考试成绩数据集的随机示例。我们将引入异常值，将其可视化，然后演示异常值处理如何影响简单线性回归模型的性能。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# Generate random student exam scores
np.random.seed(42)
num_students = 50
exam_scores = np.random.normal(70, 10, num_students)

# Introduce an outlier
outlier_index = np.random.randint(0, num_students)
exam_scores[outlier_index] = 120  # Introducing an outlier

# Visualize the data
plt.scatter(range(num_students), exam_scores, label='Original Data')
plt.xlabel('Student ID')
plt.ylabel('Exam Scores')
plt.title('Distribution of Exam Scores with Outlier')
plt.legend()
plt.show()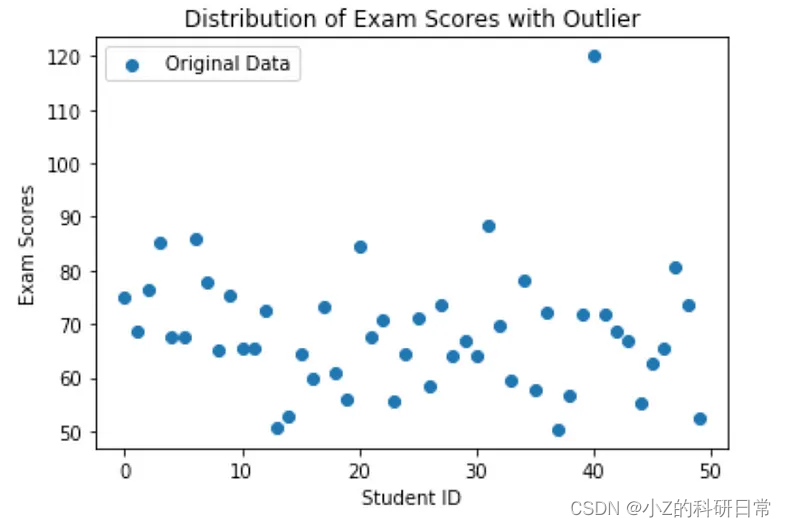

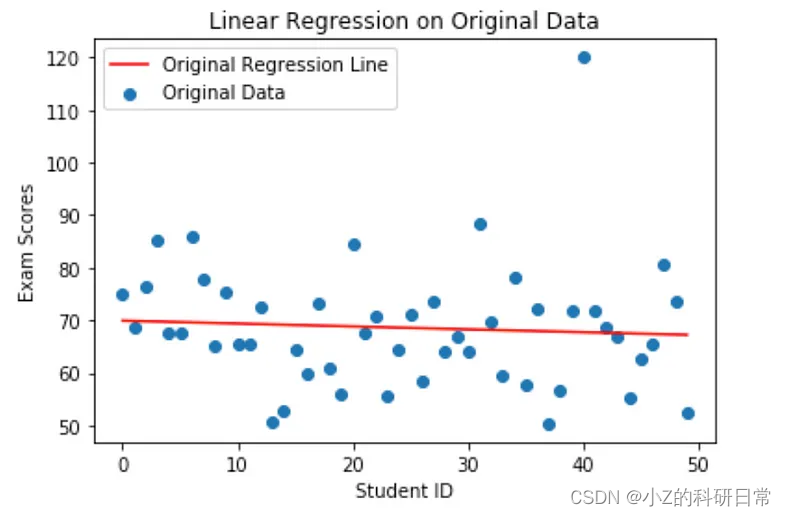
# Original linear regression model
X = np.arange(num_students).reshape(-1, 1)
y = exam_scores.reshape(-1, 1)

model = LinearRegression()
model.fit(X, y)

# Predictions on original data
predictions_original = model.predict(X)

# Calculate original mean squared error
mse_original = mean_squared_error(y, predictions_original)

#print(f"Original Mean Squared Error: {mse_original}")

plt.scatter(X, y, label='Original Data')
plt.plot(X, predictions_original, color='red', label='Original Regression Line')
plt.xlabel('Student ID')
plt.ylabel('Exam Scores')
plt.title('Linear Regression on Original Data')
plt.legend()
plt.show()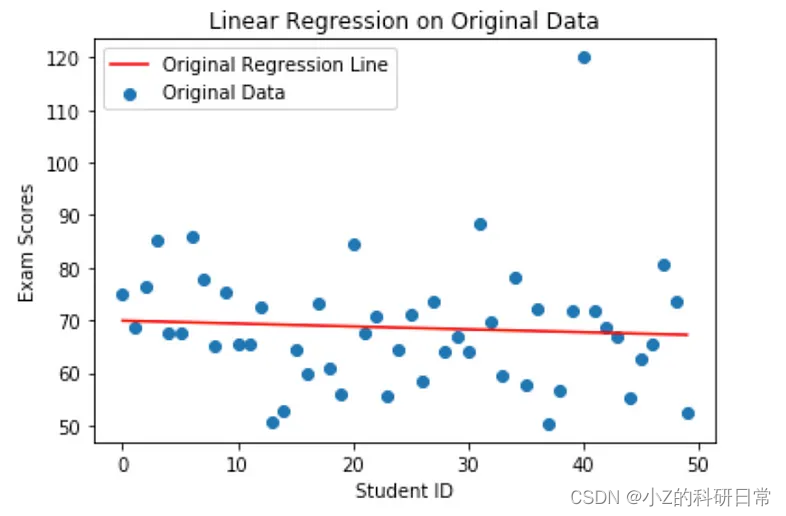

# Impute outliers with median
exam_scores_no_outlier = impute_outliers(exam_scores, method='median')

# Fit a linear regression model to the data without outliers
y_no_outlier = exam_scores_no_outlier.reshape(-1, 1)

model_no_outlier = LinearRegression()
model_no_outlier.fit(X, y_no_outlier)

# Predictions on data without outliers
predictions_no_outlier = model_no_outlier.predict(X)

# Calculate mean squared error after outlier treatment
mse_no_outlier = mean_squared_error(y_no_outlier, predictions_no_outlier)

#print(f"Mean Squared Error after Outlier Treatment: {mse_no_outlier}")
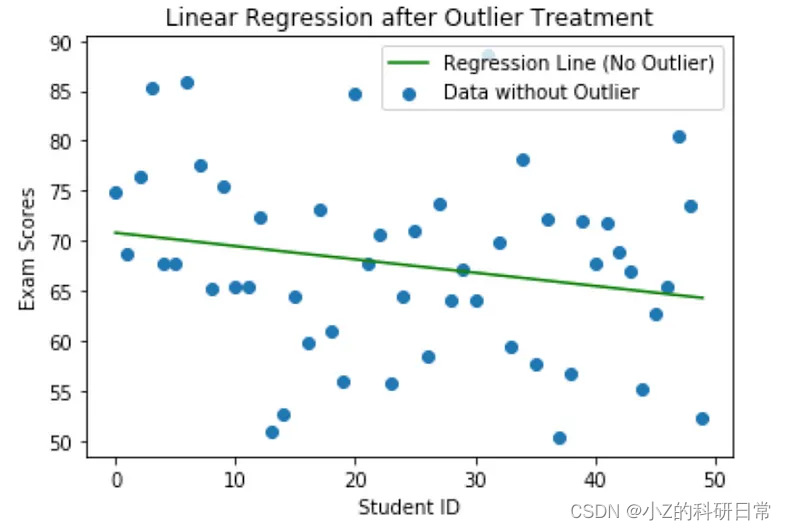
plt.scatter(X, y_no_outlier, label='Data without Outlier')
plt.plot(X, predictions_no_outlier, color='green', label='Regression Line (No Outlier)')
plt.xlabel('Student ID')
plt.ylabel('Exam Scores')
plt.title('Linear Regression after Outlier Treatment')
plt.legend()
plt.show()