文章目录
- 前言
- 数组创建
- 切片索引
- 索引
- 遍历
- 切片
- 编程练习
- 总结
前言
本篇将介绍数据处理 Numpy 库的一些基本使用技巧,主要内容包括 Numpy 数组的创建、切片与索引、基本运算、堆叠等等。
数组创建
在 Python 中创建数组有许多的方法,这里我们使用 Numpy 中的arange方法快速的新建一个数组:
import numpy as np
a = np.arange(5)
其中import numpy as np是指引入Numpy这个库,并取别名为np。之所以取别名,是为了代码编写的方便。a=np.arange(5)是指将数值0 1 2 3 4赋值给a这个变量,这样我们就快速的创建了一个一维数组。
创建多维数组的方法是:
import numpy as np
b = np.array([np.arange(6),np.arange(6)])
这里,我们使用两个arange方法,创建了两个1x6的一维数组,然后使用numpy的array方法,将两个一维数组组合成一个2x6的二维数组。从而达到了创建多维数组的目的。
numpy创建的数组可以直接复制,具体代码示例如下:
import numpy as np
x = [y for y in range(6)]
b=np.array([x]*4)
该段代码会创建一个4*6的数组。
本关的任务是,补全右侧编辑器中 Begin-End 区间的代码,以实现创建一个m*n的多维数组的功能。具体要求如下:
函数接受两个参数,然后创建与之对应的的多维数组;
本关的测试样例参见下文。
本关设计的代码文件cnmda.py的代码框架如下:
引入numpy库
import numpy as np
定义cnmda函数
def cnmda(m,n):
'''
创建numpy数组
参数:
m:第一维的长度
n: 第二维的长度
返回值:
ret: 一个numpy数组
'''
ret = 0
# 请在此添加创建多维数组的代码并赋值给ret
#********** Begin *********#
ret = np.zeros((m, n))
#********** End **********#
return ret
切片索引
索引
ndarray的索引其实和python的list的索引极为相似。元素的索引从0开始。代码如下:
import numpy as np
a中有4个元素,那么这些元素的索引分别为0,1,2,3
a = np.array([2, 15, 3, 7])
打印第2个元素
索引1表示的是a中的第2个元素
结果为15
print(a[1])
b是个2行3列的二维数组
b = np.array([[1, 2, 3], [4, 5, 6]])
打印b中的第1行
总共就2行,所以行的索引分别为0,1
结果为[1, 2, 3]
print(b[0])
打印b中的第2行第2列的元素
结果为5
print(b[1][1])
遍历
ndarray的遍历方式与python的list的遍历方式也极为相似,示例代码如下:
import numpy as np
a = np.array([2, 15, 3, 7])
使用for循环将a中的元素取出来后打印
for element in a:
print(element)
根据索引遍历a中的元素并打印
for idx in range(len(a)):
print(a[idx])
b是个2行3列的二维数组
b = np.array([[1, 2, 3], [4, 5, 6]])
将b展成一维数组后遍历并打印
for element in b.flat:
print(element)
根据索引遍历b中的元素并打印
for i in range(len(b)):
for j in range(len(b[0])):
print(b[i][j])
切片
ndarray的切片方式与python的list的遍历方式也极为相似,对切片不熟的同学也不用慌,套路很简单,就是用索引。
假设想要将下图中紫色部分切片出来,就需要确定行的范围和列的范围。由于紫色部分行的范围是0到2,所以切片时行的索引范围是0:3(索引范围是左闭右开);又由于紫色部分列的范围也是0到2,所以切片时列的索引范围也是0:3(索引范围是左闭右开)。最后把行和列的索引范围整合起来就是0:3, 0:3。当然有时为了方便,0可以省略,也就是[:3, :3]。
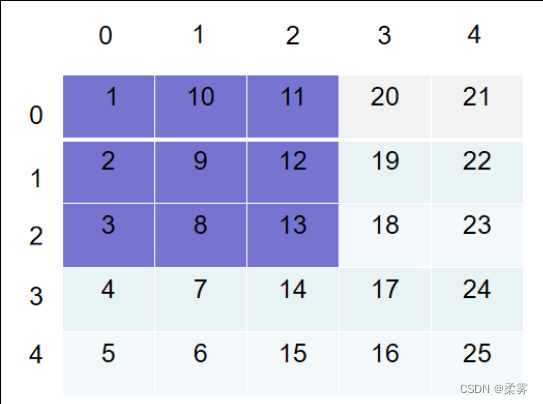
切片示例代码如下:
import numpy as np
a中有4个元素,那么这些元素的索引分别为0,1,2,3
a = np.array([2, 15, 3, 7])
'''
将索引从1开始到最后的所有元素切片出来并打印
结果为[15 3 7]
'''
print(a[1:])
'''
将从倒数第2个开始到最后的所有元素切片出来并打印
结果为[3 7]
'''
print(a[-2:])
'''
将所有元素倒序切片并打印
利用第三个参数修改索引步长,默认为1,设置-1为倒序
结果为[ 7 3 15 2]
'''
print(a[::-1])
b是个2行3列的二维数组
b = np.array([[1, 2, 3], [4, 5, 6]])
'''
将第2行的第2列到第3列的所有元素切片并打印
结果为[[5 6]]
'''
print(b[1:, 1:3])
'''
将第2列到第3列的所有元素切片并打印
结果为[[2 3]
[5 6]]
'''
print(b[:, 1:3])
编程练习
平台会对你编写的代码进行测试。你只需按要求完成get_roi(data, x, y, w, h)函数即可。其中:
data:待提取ROI的原始图像数据(其实就是个二维数组),类型为ndarray;
x: ROI的左上角顶点的行索引,类型为int;
y: ROI的左上角顶点的列索引,类型为int;
w: ROI的宽,类型为int;
h: ROI的高,类型为int。
测试用例是一个字典,字典中image部分表示原始图像的像素数据,x部分表示ROI的左上角顶点的行索引,y部分表示ROI的左上角顶点的列索引,w部分表示ROI的宽,h部分表示ROI的高。
测试输入:
{‘image’:[[1, 2, 255, 255, 0], [255, 255, 0, 0, 3]], ‘x’:0, ‘y’:1, ‘w’:2, ‘h’:1}
预期输出:
[[ 2 255 255] [255 0 0]]
import numpy as np
def get_roi(data, x, y, w, h):
'''
提取data中左上角顶点坐标为(x, y)宽为w高为h的ROI
:param data: 二维数组,类型为ndarray
:param x: ROI左上角顶点的行索引,类型为int
:param y: ROI左上角顶点的列索引,类型为int
:param w: ROI的宽,类型为int
:param h: ROI的高,类型为int
:return: ROI,类型为ndarray
'''
#********* Begin *********#
roi = data[x:x+h+1, y:y+w+1]
return roi
#********* End *********#
总结
以上就是对机器学习中的分片,切割,遍历的介绍。