智能驾驶规划控制理论学习02-基于搜索的路径规划方法

一、路径搜索问题

二、图论基础

三、图搜索方法

1、广度优先搜索（BFS）

bfs与dfs的区别

bfs的搜索过程

bfs的算法实现

2、迪杰斯特拉算法（Dijkstra）

核心思想

优先级队列

Dijkstra搜索过程

Dijkstra优缺点分析

3、A*算法

核心思想

A*搜索过程

启发式函数

总结

动态规划

一、路径搜索问题

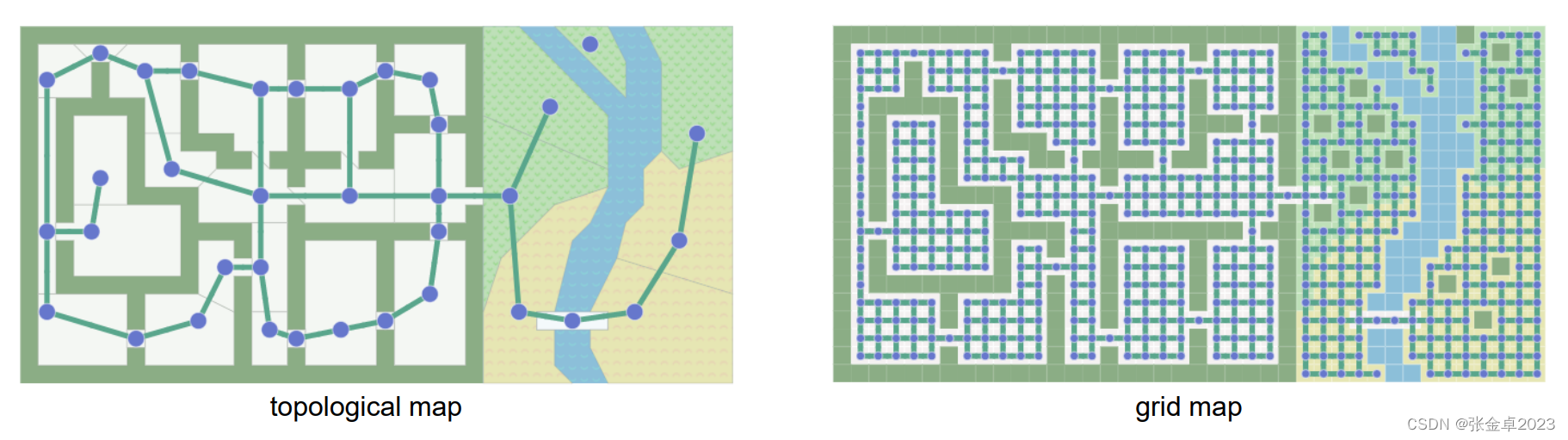
当我们要搜索一个从起到到终点的最优路径时，要思考何为最优？是从距离角度、时间角度还是其他方面。为了找到一条这样的路径，我们通常会使用一种图像搜索算法，这样地图就可以作为一个图表进行使用。

对于这种路径搜索问题，将图表上的一系列位置作为节点、它们之间的连线以及起点终点（拓扑地图信息）作为输入，得到的输出是由节点和边构成的网格地图。

二、图论基础

在图论中可以将图简单分为无向图(Undirected Graph)、有向图(Directed Graph)和权重图(Weighted Graph)。

在图论中，图由顶点（vertices）和边（edges）组成。顶点代表图中的个体或实体，而边表示顶点之间的关系或连接。这种连接可以是有向的或无向的，具体取决于图的类型和定义。

在图论中，图的权（Weight）指的是在图的边上赋予的一个数值或度量，用于表示顶点之间的关系或连接的强度、距离、成本等信息。

三、图搜索方法

本节主要介绍图搜索中常用的算法：广度优先算法（BFS）、迪杰斯特拉算法和A*算法。

1、广度优先搜索（BFS）

bfs与dfs的区别

bfs是先把本节点所连接的所有节点遍历一遍，走到下一个节点的时候，再把连接节点的所有节点遍历一遍，搜索方向更像是四面八方的搜索过程。
深度优先搜索是向一个方向去搜，不到黄河不回头，直到遇到绝境了，搜不下去了，再换方向（换方向的过程就涉及到了回溯）。

相比较而言，广搜的搜索方式就适合于解决两个点之间的最短路径问题。

bfs的搜索过程

这里利用队列的方式对bfs算法的搜索过程进行介绍，一开始先将起始节点入队，利用队列先进先出的特点在起始节点出队时将与起始节点相连的其他节点以此入队，然后继续重复上述的过程，再将队首元素弹出，将与之相邻的未访问过的节点依次添加入队，循环直到遇到目标节点或队列为空。

bfs的算法实现

在代码随想录（新更新篇）中有介绍过bfs苏娜发的C++实现，这里就直接引用了。

int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 表示四个方向
// grid 是地图，也就是一个二维数组
// visited标记访问过的节点，不要重复访问
// x,y 表示开始搜索节点的下标
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
    queue<pair<int, int>> que; // 定义队列
    que.push({x, y}); // 起始节点加入队列
    visited[x][y] = true; // 只要加入队列，立刻标记为访问过的节点
    while(!que.empty()) { // 开始遍历队列里的元素
        pair<int ,int> cur = que.front(); que.pop(); // 从队列取元素
        int curx = cur.first;
        int cury = cur.second; // 当前节点坐标
        for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历
            int nextx = curx + dir[i][0];
            int nexty = cury + dir[i][1]; // 获取周边四个方向的坐标
            if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 坐标越界了，直接跳过
            if (!visited[nextx][nexty]) { // 如果节点没被访问过
                que.push({nextx, nexty});  // 队列添加该节点为下一轮要遍历的节点
                visited[nextx][nexty] = true; // 只要加入队列立刻标记，避免重复访问
            }
        }
    }

}

bfs向各个方向搜索的可能性都相同，如果各边的权重都为1，那么使用BFS算法进行搜索就是最优的。但是在大多数情况下，往往各个方向的运动都会有不同的代价值（权重），如何对这些具有不同权重的图进行处理就就要引出下面的算法了。

2、迪杰斯特拉算法（Dijkstra）

核心思想

与BFS直接将队列中弹出元素相连的所有元素都存入队列，Dijkstra利用贪心的思想每次选择都是累计代价值最小的节点进行相加。

具体来说，Dijkstra创建了一个先变量g(n)，以此来代替从起始节点到达当前节点所消耗的代价值，每次从开放集openset中寻找累计大价值最小的节点进行相加，而不是访问队列中的第一个元素。

优先级队列

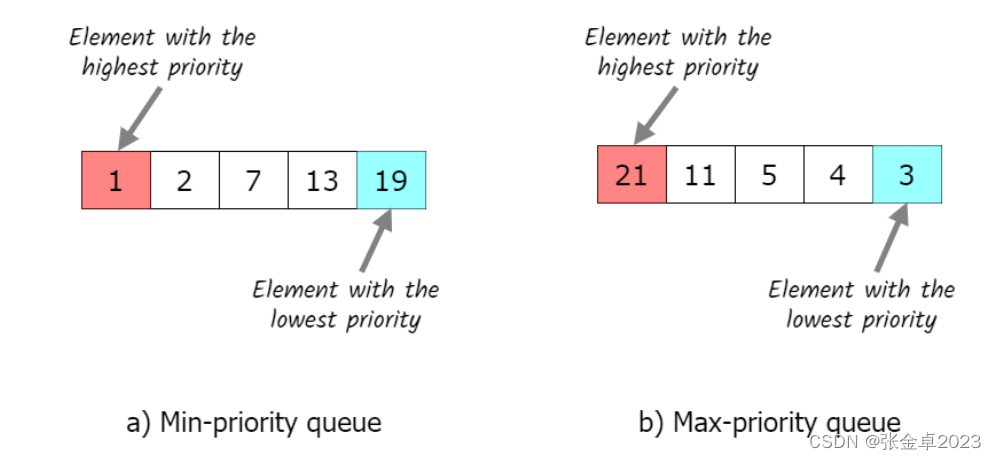
优先级队列中每一个元素都有着与之对应的优先级。在优先级队列中，优先级高的元素会比优先级低的元素先访问。

Dijkstra搜索过程

输入：一个图表（包含节点和路径的集合）和一个起始节点；

输出：到任意节点的最短路径。

用伪代码进行简洁描述：

Algorithm Dijkstra(G, start):
    let open_list be pirority queue
    open_list.push(start, 0)
    g[start] := 0

    while (open_list is not empty):
        current := open_list.pop()
        mark current as visited
        if current is the goal:
            return current
        for all unvisited neighbours next of current in Graph G:
            next_code := g[current] + cost(current, next)
            if next is not in open_list:
                open_list.push(next, next_cost)
            else:
                if g[next] > next_cost:
                    g[next] := next_cost

先创建一个优先级队列open_list，将起始节点存入优先级队列，并设置累计代价函数的初值为0，然后进行循环（循环终止条件设为优先级队列非空），在循环中每次弹出优先级队列中的节点就要判断是否是目标节点，如果是目标节点就直接返回，若不是就要将弹出节点设为已访问节点，并对图表中当前弹出节点周围的其余邻居节点进行判断，若是未访问节点则直接存入优先级队列，若已访问则进行累计代价函数更新。

Dijkstra优缺点分析

优点：

Dijkstra算法可以寻找到起始节点到图表上其他所有节点的最短路径；
Dijkstra孙发满足最优原则。

缺点：

该算法始终在优先级队列中寻找最短路径，而不考虑方向或距离目标的远近。因此，若使用它来搜索一个特定目标的最短路径时，并不高效。

3、A*算法

核心思想

A*算法在Dijkstra算法的基础上引入启发式函数作为对目标节点的引导，从而提高了搜索的效率。

启发式函数h(n)表示从节点n到目标的估计代价。使用f-score来评估每个节点的代价：f(n) = g(n) + h(n)，然后在优先级队列中选取f-score最小的节点，而不是Dijkstra中的g-score。

A*搜索过程

Algorithm Astar(G, start):
    let open_list be priority queue
    g[start] := 0
    f[start] = g[start] + h[start]
    open_list.push(start, f[start])
    
    while (open_list is not empty):
        current := open_list.pop()
        mark current as visited
        if current is the goal:
            return current
        for all unvisited neighbours next of current in Graph G:
            next_cost := g[current] + cost(current, next)
            if next is not in open_list:
                open_list.push(next, next_cost + h[next]
            else:
                if g[next] > next_cost
                    g[next] = next_cost
                    f[next] = next_cost + h[next]

依然是创建一个优先级队列，并对g(n)和f(n)赋初值（假设启发式函数h(n)）已知，再将初始节点和其对应的f-socre存入优先级队列，然后开始进入循环（循环的终止条件式队列非空），弹出队列中的节点，将其标志为已访问，若该节点为目标节点直接返回，否则要对其在图表中的邻居节点进行判断，若邻居节点未被访问则存入优先级队列中，存放时对应的代价函数还要加上h-score，若已访问则进行代价值更新。

启发式函数

A*算法有别于Dijkstra的最大之处就在于启发算法的加入，但是在路径搜索问题中没有特定的启发式函数，因为每一种情况都是不同的。

要注意启发式函数不能过高的估计代价值，只要启发式函数提供的估计值小于真实值，那么A*总会找到一条最优的路径并且通常比Dijkstra效率高。

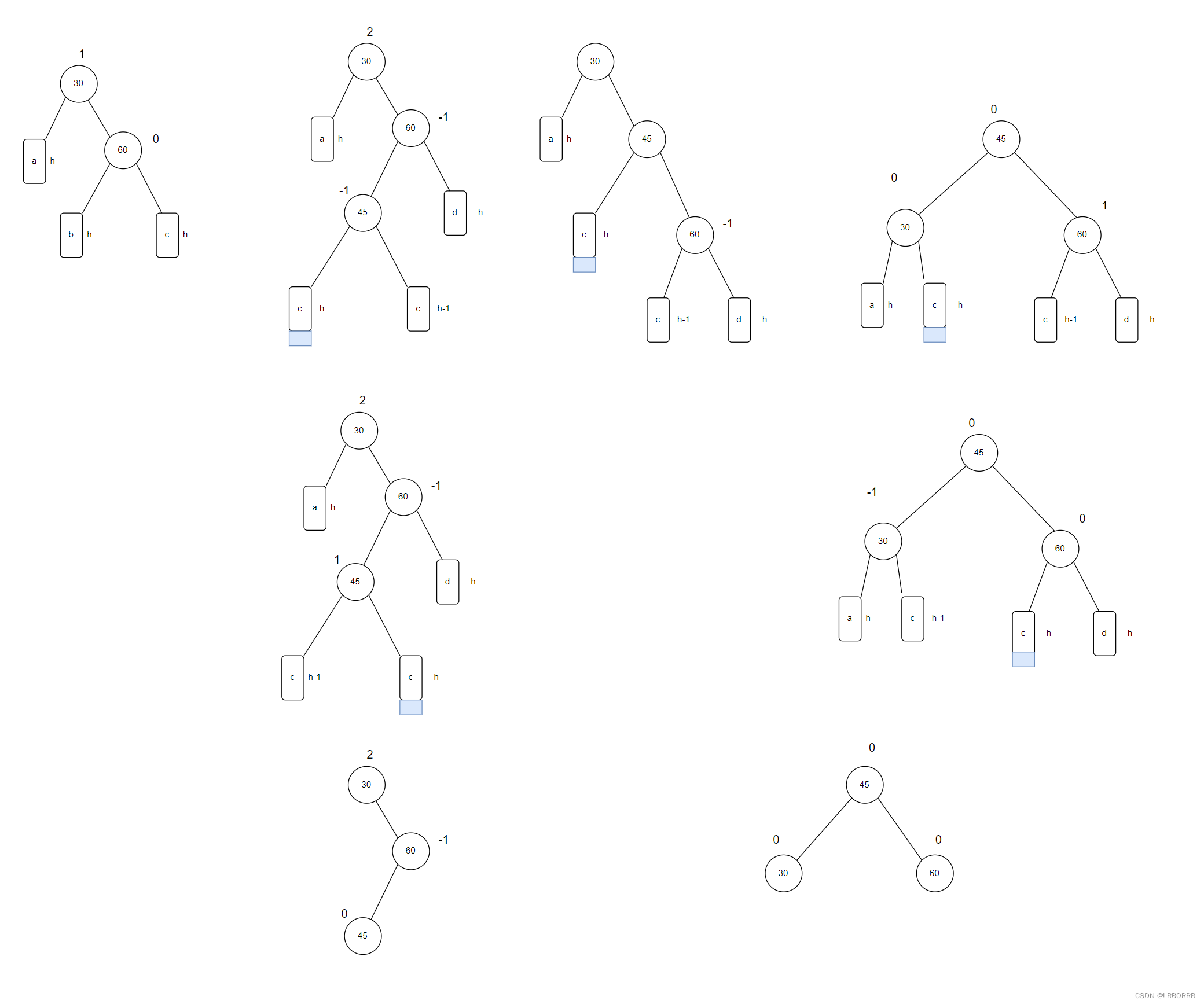
如果启发式函数的代价值估计过高了，会产生什么影响呢，以下图为例：

图中所示的B节点对应的启发式函数估计的代价值高于其真实值，因此C节点的f-score高于B节点的f-score，因此会错误地优先选择C节点通过，但实际上B节点才是更优的选择。

A*搜索的效率与精度也取决于启发式函数的选择，主要有以下四种情况：

h(n) = 0：此时f-socre = g-score A*算法退化为Dijkstra算法；
h(n) < cost(n, goal)：A*满足最优性，搜索效率上高于Dijkstra算法；
h(n) = cost(n, goal)：A*满足最优性，并且达到最高搜索效率；
h(n) > cost(n, goal)：启发式函数高估了实际代价，不具有最优性。

总结

BFS在各个方向上的搜索可能性相同，并且如果各边权重为1，bfs搜索得到的路径满足最优性；
Dijkstra算法利用贪心的思想选择累计代价值最低的节点，并且能够在有权图中表现出最优性，如果各边权重为1，那么Dijkstra搜索得到的路径和BFS搜索得到的相同。
A*是Dijkstra的改进，通过加入启发式函数提高搜索的效率，启发式函数的设计会直接影响到搜索的效率和精度。