背包最大重量为4。
有物品3件,分别有其质量和价值。
vector<int> weight={1,3,4};
vector<int> value={15,20,30};
int bag=4;问背包能背的物品最大价值是多少?
这是标准的动态规划问题,每一个问题鱼鳍前面的子问题相联。
目录
表格
分析
递推公式
横竖不同遍历(个人分析)
表格
我们画一个表格就好理解了,在表格里,只需要记住,每个表格是当前的最优解(价值)。
物品(重量,价值)
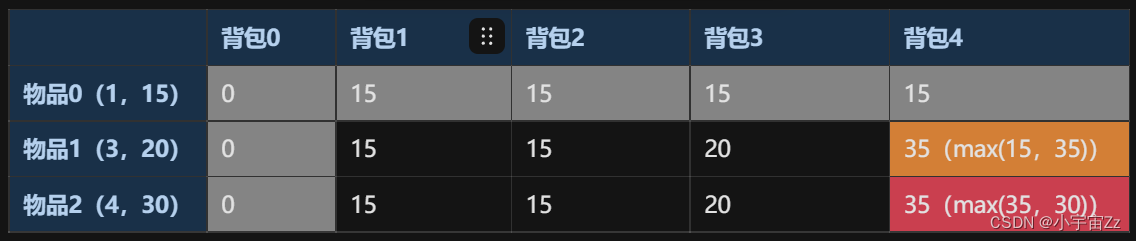
分析
对于每个表格,其最大价值只有放与不放该物品,若放其价值即为该物品价值加上(背包质量-物品质量)的背包的最优解。
- 我们举个例子:
以橙表格为例子
背包4如果不拿物品1,其最大价值就为他的上面一格即15价值,
如果拿物品1,其最大价值就为物品1的价值(20)加上背包剩余空间的最大价值。就相当于背包1(4-3)的最大价值,即(15),相加即为35.
两者对比发现拿物品1总价值最大,所以背包4在可以拿物品0~1的情况下,其最大价值(最优解)为35。
- 我们再举个例子:
以红表格为例子:
如果不拿物品2,其最大价值为其上一格价值35。
如果拿物品2,其最大价值为物品2价值(30)加上背包剩余空间最大价值,相当于背包0的最大价值(0),相加为30。
两者对比发现不拿物品2价值更高,即背包4在可选物品0~2的情况下,最大价值(最优解)为35。
递推公式
由此,我们就可以推导递推公式了。
dp[i][j]=max(dp[i-1][j],value[i]+dp[value.size()-1][j-weight[i]]);当然还有一种情况,就是当前物品该背包装不下,那么就直接继承其上一个格子即可。
横竖不同遍历(个人分析)
确定完dp初始值和递推公式后,我们要确定遍历顺序了,我们有两种遍历顺序,一种是一行一行遍历,还有一种是一列一列遍历,对于这两种遍历,结果是一样的,但在遍历过程中,有几处不一样。(可忽略,不影响)

以橙色格子为例,他的最大价值是
max(dp[i-1][j],value[i]+dp[i][j-weight[i]]);其中
value[i]+dp[i][j-weight[i]]中的剩余空间最大价值,即为背包3的最优解,但是我们知道背包3的最优解应该是背包3最下面一个格子(即考虑了所有物品的最优解),但是我们却是
dp[i][j-weight[i]]即背包3在当前行的最优解,这样按常识来讲很有可能会出错,而且这样两种写法虽然结果一样,但列出的表格里面个别数据会不一样。
例如这个表格,橙色格子如果只考虑物品0~i,其最大价值应该是35,但是其小背包3(背包4-物品1质量)最优解为30,这样就为50了
dp[value.size()-1][j-weight[i]];
//value.size()-1为最下面一格但实际上这两种都是对的,只是思维方式不一样,
dp[i][j-weight[i]]是每个背包只考虑物品0~i时的最优解,不考虑下面的物品。即每一个格子都是物品0~i的最优解,这样也符合我们正常的思维逻辑。
而如果看背包3最下面一个格子的话(即考虑了所有物品的最优解),背包4的当前格子数据可能会更大些,但是这样这个格子的说法就有一点说不过去了,到底是物品0~i的最优解,还是考虑所有物品的最优解呢,那这样背包4这个格子就是自己还没考虑下面的物品,但其小背包却考虑了@W@,虽然最后结果是一样的(最后结果是考虑所有物品,所以两种情况的最后一行是一样的)
当然,如果真的想考虑其剩余空间真正的最优解,那只能竖着写了,不然其小背包的最下面一个格子就属于还没遍历的格子,为0。
但是我还是建议一行一行写,这样,每一个格子就是考虑物品0~i的最优解,不会矛盾了。