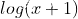一、本周周赛总结

-只会2.5题。

• T1 模拟。
• T2 模拟。
• T3 位运算。
• T4 二分+差分+前缀和。

二、 [Easy] 2525. 根据规则将箱子分类

链接: 2525. 根据规则将箱子分类

1. 题目描述

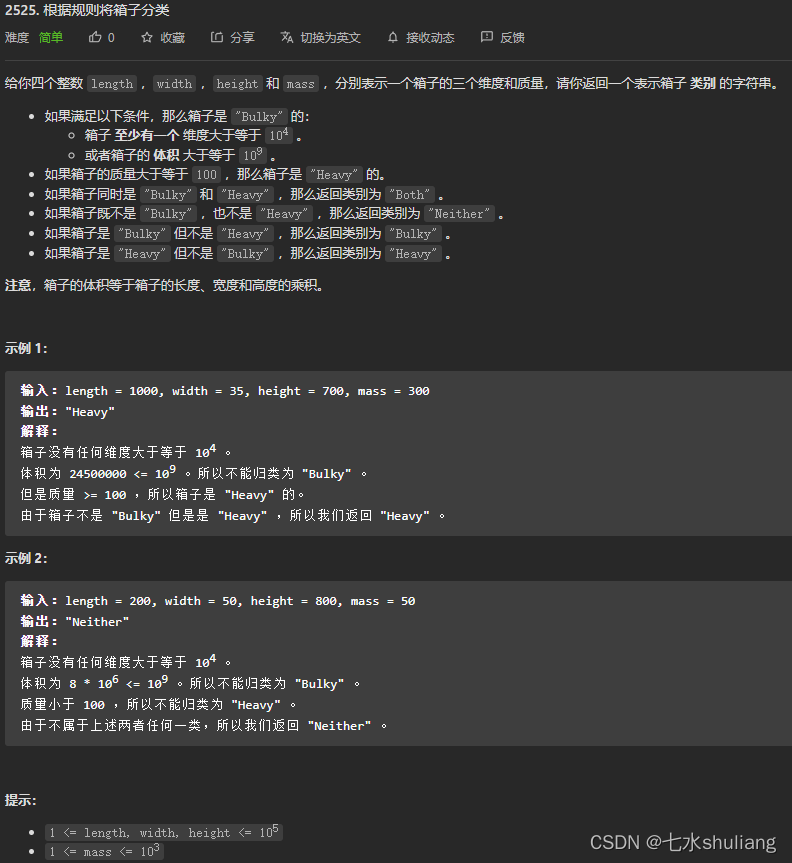
2. 思路分析

按题意分类即可。

• 但我搞了状压。

3. 代码实现

class Solution:
    def categorizeBox(self, length: int, width: int, height: int, mass: int) -> str:
        ans = 0
        if length>=10**4 or width>=10**4 or height>=10**4 or length*width*height>=10**9:
            ans |= 1
        if mass>= 100:
            ans |= 2
        return ['Neither','Bulky','Heavy','Both'][ans] 

三、[Medium] 2526. 找到数据流中的连续整数

2. 思路分析

用一个cnt记录最后连续的value即可，如果不是value就置0.

3. 代码实现

class DataStream:

    def __init__(self, value: int, k: int):
        self.value = value
        self.k = k
        self.a = 0


    def consec(self, num: int) -> bool:
        if num != self.value:
            self.a = 0
            return False
        self.a += 1
        return self.a >= self.k

四、[Medium]2527. 查询数组 Xor 美丽值

链接: 2527. 查询数组 Xor 美丽值

1. 题目描述

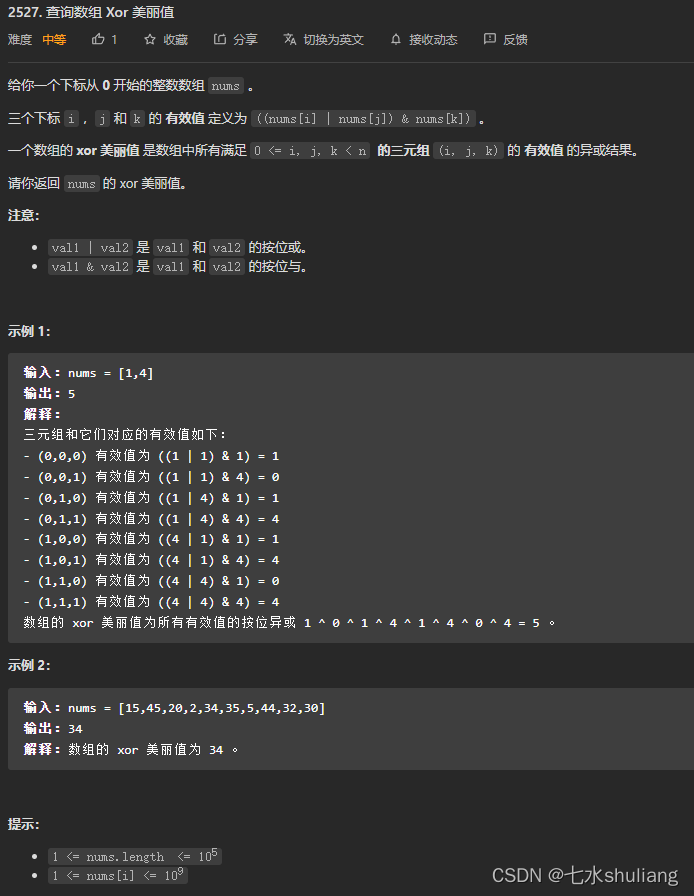
2. 思路分析

• 位运算每一位互相不影响，因此可以拆位处理。
• 对于每一位，不是0就是1，由于最后是异或，我们只需要考虑最后运算里，(a|b)&c有多少个1.
• 如果有偶数个1，异或起来就是0；奇数个1，异或就是1.
• 那么c必须是1，a和b至少有1个1(不能都是0)。
• 在nums中，当前位有y个1，x个0，显然x=n-y
• 则最终1的个数 :

  •   ones = (n^2^-x^2^)y = (n^2^-(n-y)^2^)y = (2ny-y^2^)y
    

• 由于我们只需要看y的奇偶性，因此就看y³的奇偶性即可，和y的奇偶性一致。
• 由于我们拆位了，因此看当前位有几个1即可，异或到一起就是答案。

3. 代码实现

class Solution:
    def xorBeauty(self, nums: List[int]) -> int:
        return reduce(xor,nums)

五、[Hard] 2528. 最大化城市的最小供电站数目

链接: 2528. 最大化城市的最小供电站数目

1. 题目描述

2. 思路分析

• 这题我尝试了用IUPQ的树状数组，但是TLE了，23/30,复杂度nlognlogU。这个复杂度cpp是能过得，py被卡了。
• 只好用nlogU的做法。

---

• 先用前缀和计算实际上每个城市有几个站覆盖。
• 我们的目的是把k个电站建到当前电力比较弱的地方，加强这些弱的城市，使最后答案尽量大。
• 那么显然答案越大，越难实现；答案越小，随便建几个就实现了。
• 于是我们二分答案limit,(其中limit指加完电站后，这个城市至少覆盖了limit个电站)。
• check的过程是贪心，考虑如果station[i]<limit就在附近建电站，那么建到右侧最远的地方即可，这样这个站能贡献更多的位置。
• 那么用差分就可以做到遍历的同时计算每个位置的覆盖值。

3. 代码实现

class Solution:
    def maxPower(self, stations: List[int], z: int, k: int) -> int:
        n = len(stations)
        p = [0] + list(accumulate(stations))
        for i in range(n):
            stations[i] = p[min(i+z,n-1)+1]-p[max(i-z,0)]
        mn = min(stations[1:],default=0)
        mx = max(stations)+k


        def ok(x):
            diff = [0]*n  # 差分数组
            s = 0
            p = k
            for i,v in enumerate(stations):
                s += diff[i]  # 累计s
                delta = x - v - s  # 差多少
                if delta > 0:
                    p -= delta
                    if p < 0:
                        return True
                    s += delta  # 累计s
                    r = i + z*2                   
                    if r+1<n:
                        diff[r+1] -= delta  # 差分数组更新，由于左边再不会用到了(累计到了s)，因此只更新右边就行                    
            return False
            
        return bisect_left(range(mx+1),True,lo=mn,key=ok)-1       

六、参考链接