算法------（13）KMP

news2024/9/24 17:51:34

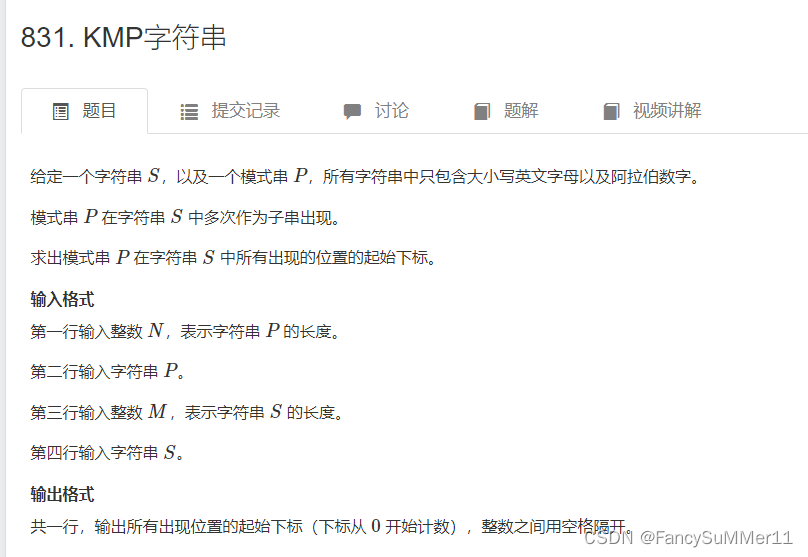
例题：（1）AcWing 831. KMP字符串 

        。。其实写完也不太理解。。随便写点吧

        KMP就是求next数组和运用next的数组的过程。相比传统匹配模式一次更新一单位距离的慢速方法，next数组可以让下表字符串一次更新n - next【n】个距离，加快了匹配速度。next【i】记录的是某字符串的前i个字符中前缀与后缀最长的匹配长度。

        对于模版中的j，我的理解是已经匹配了j个字符，因此next【i】还可以理解为对于已经匹配了i个字符的字符串来说，假如后续匹配不成立，则该字符串至少还有next【i】个字符是匹配的。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5+10,M = 1e6+10;
int ne[N];
int n,m;
char p[N],s[M];
int main()
{
    cin >> n >> p+1 >> m >> s+1;
    ne[1] = 0;
    for(int i = 2,j = 0;i<=n;i++){
        while(j && p[i] != p[j+1]) j = ne[j];
        if(p[i] == p[j+1]) j++;
        ne[i] = j;
    }
    for(int i = 1,j = 0;i<=m;i++){
        while(j && s[i] != p[j+1]) j = ne[j];
        if(s[i] == p[j+1]) j++;
        if(j == n){
            printf("%d ",i - n);
            j = ne[j];
        }
    }
    return 0;
}

练习：（1） Leetcode 459 重复的子字符串

        。。。好难啊！！！！这是easy？？？

        我们可以证明 非空字符串s可由一个子串重复多次构成 当且仅当 把两个s连接起来且去掉前面后面的各一个字符，其中仍然存在s作为新字符串的子串。 

        从前往后推很显然，从后往前推需要一定证明。显然我不会，摘抄一下Leetcode的答案。

（2） P1470 [USACO2.3] 最长前缀 Longest Prefix

         其实与KMP无关但不知道为什么加了个KMP的标签。。。没做出来。。

        跟之前做过的一些题目有些类似。dp[i]的含义为[0,i-1]个字母可以分解，因此我们枚举每一个j，只要满足[0,j-1]时能分解且[j,i-1]也在P集合内即可。对于查询[j,i-1]，由于题目说P集合内字符串长度<=10，因此我们对每一个i只需要枚举10个j即可，这样大大优化了时间。

        以及不知为什么本地跑不了。。。（问了朋友可能是文件输入输出的关系）

#include <iostream>
#include <unordered_set>
#include <string>
using namespace std;
const int N = 2e5+10;
bool dp[N];
unordered_set<string> res;
int main(int argc, char** argv) {
	string ss;
	while(cin >> ss){
		if(ss == ".") break;
		res.insert(ss);
	}
	string ans = "";
	while(cin >> ss){
		ans += ss;
	}
	dp[0] = true;
	int n = ans.length();
	for(int i = 1;i<=n;i++){
		for(int j = i;j>=max(i-10,0);j--){
			if(dp[j] && (res.find(ans.substr(j,i-j))!=res.end())){
				dp[i] = true;
				continue;
			}
		}
	}
	for(int i = n;i>=0;i--){
		if(dp[i]){
			printf("%d",i);
			break;
		}
	}
	return 0;
}

(3) P3435 [POI2006] OKR-Periods of Words

        太难了太难了。。。

        一个前缀的最大周期长度就是其长度减去其最小匹配长度，也就是其最短的共同前后缀的长度。 next数组求的是最大匹配长度，而不断递归求next数组得到的正是不为0的最小匹配长度。递归处理时可以把next数组直接更新为求得的最短长度，这样求取速度会更快。

#include <iostream>
using namespace std;
typedef long long ll;
const int N = 1000010;
char str[N];
int ne[N];
int main(int argc, char** argv) {
	int n;
	scanf("%d%s",&n,str+1);
	ne[1] = 0;
	for(int i = 2,j = 0;i<=n;i++){
		while(j && str[i] != str[j+1]) j = ne[j];
		if(str[i] == str[j+1]) j++;
		ne[i] = j;
	}
	ll ans = 0;
	for(int i = 2,j = 2;i<=n;i++,j = i){
		while(ne[j]) j = ne[j];
		if(ne[i]) ne[i] = j;
		ans += i-j;
	}
	printf("%lld",ans);
	return 0;
}

(4) Leetcode 面试题17.17 多次搜索

          对每一个smalls内的字符串求next数组，然后与big字符串进行kmp匹配。注意kmp的i返回的是字符串的最后一个字符下标。以及每一次匹配都要先清空next数组。

class Solution {
    int ne[1010];
    vector<vector<int>> res;
public:
    void next(string str){
        char x[1010];
        int n = str.length();
        for(int i = 1;i<=n;i++) x[i] = str[i-1]; 
        for(int i = 2,j = 0;i<=n;i++){
            while(j && x[i] != x[j+1]) j = ne[j];
            if(x[i] == x[j+1]) j++;
            ne[i] = j;
        }
    }
    vector<int> get(string a,string b){
        char x[1010],y[1010];
        int n = a.length(),m = b.length();
        for(int i = 1;i<=n;i++) x[i] = a[i-1];
        for(int i = 1;i<=m;i++) y[i] = b[i-1];
        vector<int> ans;
        for(int i = 1,j = 0;i<=n;i++){
            while(j && x[i] != y[j+1]) j = ne[j];
            if(x[i] == y[j+1]) j++;
            if(j == m){
                ans.push_back(i-m);
                j = ne[j];
            }
        }
        return ans;
    }
    vector<vector<int>> multiSearch(string big, vector<string>& smalls) {
        int n = smalls.size();
        for(int i = 0;i<n;i++){
            if(smalls[i] == ""){
                res.push_back({});
                continue;
            }
            memset(ne,0,sizeof(ne));
            next(smalls[i]);
            res.push_back(get(big,smalls[i]));
        }
        return res;
    }
};

(5) Leetcode 3036 匹配模式数组的子数组数目

        做出来的第一个Hard题！虽然完全不是自己想出来的！！。。。

        把nums转化为跟pattern数组一样模式的长度为n-1的数组，此题便转化为求nums数组中有几个子数组为pattern数组，这样一来直接用kmp匹配即可。转化这一步还是挺难想到的。

class Solution {
    int x[1000100],y[1000100],ne[1000100];// x,y 1-n
public:
    int countMatchingSubarrays(vector<int>& nums, vector<int>& pattern) {
       int n = nums.size()-1,m = pattern.size();
       for(int i = 0;i<n;i++){
           if(nums[i] < nums[i+1]) x[i+1] = 1;
           else if(nums[i] == nums[i+1]) x[i+1] = 0;
           else x[i+1] = -1;
       } 
       for(int i = 1;i<=m;i++){
           y[i] = pattern[i-1];
       } 
       for(int i = 2,j = 0;i<=m;i++){
           while(j && y[i] != y[j+1]) j = ne[j];
           if(y[i] == y[j+1]) j++;
           ne[i] = j; 
       }
       int ans = 0;
       for(int i = 1,j = 0;i<=n;i++){
           while(j && x[i] != y[j+1]) j = ne[j];
           if(x[i] == y[j+1]) j++;
           if(j == m){
               ans++;
               j = ne[j];
           }
       }
       return ans;
    }
};

(6) Leetcode 3037.在无限流中寻找模式

         做出的第二道Hard题，想出了匹配方式但是在优化上栽了！不过还算可以！

        由于是无限流，所以每次更新就匹配一次肯定会超时，因此用vector处理，由于next数组是确定的，因此每次不用从头匹配，只需要一个一个进行匹配即可。

/**
 * Definition for an infinite stream.
 * class InfiniteStream {
 * public:
 *     InfiniteStream(vector<int> bits);
 *     int next();
 * };
 */
class Solution {
    int ne[110000];
    vector<int> p,q;
public:
    int findPattern(InfiniteStream* stream, vector<int>& pattern) {
        p.push_back(0);
        q.push_back(0);
        int r = 0,m = pattern.size();
        for(int i = 1;i<=m;i++){
            q.push_back(pattern[i-1]);
        }
        for(int i = 2,j = 0;i<=m;i++){
            while(j && q[i] != q[j+1]) j = ne[j];
            if(q[i] == q[j+1]) j++;
            ne[i] = j;
        }
        int i = 1,j = 0;
        while(1){
            p.push_back(stream->next());
            while(j && p[i] != q[j+1]) j = ne[j];
            if(p[i] == q[j+1]) j++;
            if(j == m) return i-m;
            i++;
        }
    }
};

(7) Leetcode 3008.找出数组中的美丽下标

         Hard被卡了。。

        匹配用kmp，后续查找时的优化思路为对a中每一个下标数组，在b的下标数组二分查找第一个大于等于它的数，如果这个数存在则返回其与a中对应下标的差，和其前面一个与a中对应下标的差，如果满足则返回。

class Solution {
    char p[500100],q[500100],r[500010];
    int ne1[500100],ne2[500100];
public:
    vector<int> beautifulIndices(string s, string a, string b, int k) {
        vector<int> res;
        vector<int> res1,res2;
        int n = a.length(),m = b.length(),o = s.length();
        for(int i = 1;i<=n;i++) p[i] = a[i-1];
        for(int i = 1;i<=m;i++) q[i] = b[i-1];
        for(int i = 1;i<=o;i++) r[i] = s[i-1];
        for(int i = 2,j = 0;i<=n;i++){
            while(j && p[i] != p[j+1]) j = ne1[j]; 
            if(p[i] == p[j+1]) j++; 
            ne1[i] = j;
        }
        for(int i = 2,j = 0;i<=m;i++){
            while(j && q[i] != q[j+1]) j = ne2[j]; 
            if(q[i] == q[j+1]) j++; 
            ne2[i] = j;
        }
        for(int i = 1,j = 0;i<=o;i++){
            while(j && r[i] != p[j+1]) j = ne1[j]; 
            if(r[i] == p[j+1]) j++; 
            if(j == n){
                res1.push_back(i-n);
                j = ne1[j];
            } 
        }
        for(int i = 1,j = 0;i<=o;i++){
            while(j && r[i] != q[j+1]) j = ne2[j]; 
            if(r[i] == q[j+1]) j++; 
            if(j == m){
                res2.push_back(i-m);
                j = ne2[j];
            } 
        }
        int c1 = res1.size(),c2 = res2.size();
        for (int i: res1) {
            auto it = lower_bound(res2.begin(), res2.end(), i);
            if (it != res2.end() && *it - i <= k ||
                it != res2.begin() && i - *--it <= k) {
                res.push_back(i);
            }
        }
        return res;
    }
};

（8） Leetcode 758.字符串中的加粗单词

         没啥难的。。挑错时间太长所以贴上来羞辱一下自己。。

        kmp加合并区间。首先先对words每一个字符串求next然后与s进行匹配，求出每一个需要加粗的区间。由于这些区间存在重叠而导致标签数过多，因此要求最小的标签数就需要合并区间。

class Solution {
    int ne[15];
    typedef pair<int,int> pii;
public:
    vector<pii> segs;
    vector<char> init(string x){
        vector<char> p;
        p.push_back(0);
        int n = x.length();
        for(int i = 1;i<=n;i++) p.push_back(x[i-1]);
        return p;
    }
    void next(vector<char> x){
        int n = x.size()-1;
        for(int i = 2,j = 0;i<=n;i++){
            while(j && x[i] != x[j+1]) j = ne[j];
            if(x[i] == x[j+1]) j++;
            ne[i] = j;
        }
    }
    void kmp(vector<char> x,vector<char> y){
        int n = x.size() - 1,m = y.size() - 1;
        for(int i = 1,j = 0;i<=n;i++){
            while(j && x[i] != y[j+1]) j = ne[j];
            if(x[i] == y[j+1]) j++;
            if(j == m){
                segs.push_back({i-m,i-1});
                j = ne[j];
            }
        }
    }
    string boldWords(vector<string>& words, string s) {
        int n = words.size();
        auto p = init(s);
        for(int i = 0;i<n;i++){
            memset(ne,0,sizeof(ne));
            auto q = init(words[i]);
            next(q);
            kmp(p,q);
        }
        vector<pii> res;
        sort(segs.begin(),segs.end());
        int fs = -2e9,ed = -2e9;
        for(auto seg:segs){
            int l = seg.first,r = seg.second;
            if(ed+1<l){
                if(fs!=-2e9) res.push_back({fs,ed});
                fs = l;
                ed = r;
            }
            else{
                ed = max(ed,r);
            }
        }
        if(fs!=-2e9) res.push_back({fs,ed});
        int flag = 0;
        string ans = "";
        for(auto seg:res){
            int l = seg.first,r = seg.second;
            ans += s.substr(flag,l - flag);
            ans += "<b>";
            ans += s.substr(l,r-l+1);
            ans += "</b>";
            flag = r+1;
        }
        n = s.length();
        cout <<flag;
        if(flag < n ) ans += s.substr(flag,n-flag);
        return ans;
    }
};

 （9） P2375 [NOI2014] 动物园           很难，虽然写出来了但并不完全理解。。

           在求取next数组的过程中，我们可以求取每一个i所对应的有相同的前后缀的所有子串的个数，然后再进行一次匹配，当我们递归到子串长度不重叠时，就可以得到该长度下所有的不重叠的子串有相同前后缀的个数。

#include <iostream>
#include <cstring>
using namespace std; 
const int N = 1e6+10,mod = 1e9+7;
typedef long long ll;
char p[N];
int ne[N],nums[N];
int main(int argc, char** argv) {
	int t;
	scanf("%d",&t);
	while(t--){
		scanf("%s",p+1);
		int n = strlen(p+1);
		nums[1] = 1;
		for(int i = 2,j = 0;i<=n;i++){
			while(j && p[i] != p[j+1]) j = ne[j];
			if(p[i] == p[j+1]) j++;
			ne[i] = j;
			nums[i] = nums[ne[i]] + 1;
		}
		ll res = 1;
		for(int i = 1,j = 0;i<=n;i++){
			while(j && p[i]!=p[j+1]) j = ne[j];
			if(p[i] == p[j+1]) j++;
			while(j * 2 > i) j = ne[j]; 
			res = res * (nums[j] + 1) % mod;
		}
		printf("%lld\n",res);
		for(int i = 1;i<=n;i++){
			ne[i] = 0;
			nums[i] = 0;
		} 
	}
	return 0;
}

 

        

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1483355.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Java项目layui分页中文乱码

Java项目layui分页中文乱码

【问题描述】这部分没改之前中文乱码。 【解决办法】在layui.js或者layui.all.js文件中替换共、页、条转换成Unicode码格式。 字符Unicode共&#x5171页&#x9875条&#x6761【完美解决】改完之后重新运行项目&#xff0c;浏览器F12缓存清除就好了&#xff0c;右键
阅读更多...
从键盘输入5个整数，将这些整数插入到一个链表中，并按从小到大次序排列，最后输出这些整数。

从键盘输入5个整数，将这些整数插入到一个链表中，并按从小到大次序排列，最后输出这些整数。

设节点定义如下struct Node {int Element; // 节点中的元素为整数类型struct Node * Next; // 指向下一个节点 }; 从键盘输入5个整数&#xff0c;将这些整数插入到一个链表中&#xff0c;并按从小到大次序排列&#xff0c;最后输出这些整数。注释那段求指出错误&#xff0c;求解…
阅读更多...
【QT+QGIS跨平台编译】之六十二：【QGIS_CORE跨平台编译】—【错误处理：未定义类型QgsPolymorphicRelation】

【QT+QGIS跨平台编译】之六十二：【QGIS_CORE跨平台编译】—【错误处理：未定义类型QgsPolymorphicRelation】

文章目录 一、未定义类型QgsPolymorphicRelation二、解决办法一、未定义类型QgsPolymorphicRelation 报错信息： 错误原因为，使用了未定义类型 QgsPolymorphicRelation 二、解决办法 QgsRelation.h文件中 ①注释第36行： //class QgsPolymorphicRelation;②注释第414行： …
阅读更多...
leetcode括号生成

leetcode括号生成

题目描述 解题思路 首先看到题目&#xff0c;一开始是并没有思路的。这时候可以在纸上进行演算一下结果。当只有一对括号的时候&#xff0c;我们可以得知结果[“()”],当有两对括号的时候&#xff0c;我们可以发现&#xff0c;括号在第一个基础上&#xff0c;要么在括号内部出…
阅读更多...
Java中心校智慧校园智慧班牌物联网平台源码

Java中心校智慧校园智慧班牌物联网平台源码

目录 智慧班牌 班牌首页 班级信息 课表信息 视频 图片 进离校管理 人脸登录页 学生个人中心 请假管理 成绩管理 家长留言 学生绑卡 学生评价 系统设置 通知管理 值日管理 倒计时 班级德育 班牌模式 1.课堂授课模式 2.家长会签到模式 3.考场模式 4.班级…
阅读更多...
MySQL：错误ERROR 1045 (28000)详解

MySQL：错误ERROR 1045 (28000)详解

1.问题说明 有时候我们登录Mysql输入密码的时候&#xff0c;会出现这种情况&#xff1a; mysql -u root -p Enter Password > ‘密码’ 错误&#xff1a;ERROR 1045 (28000): Access denied for user ‘root’‘localhost’ (using password: YES) 或者&#xff1a;错误…
阅读更多...
本届挑战赛季军方案：构建由大模型辅助的基于多模态数据融合的异常检测、根因诊断和故障报告生成系统

本届挑战赛季军方案：构建由大模型辅助的基于多模态数据融合的异常检测、根因诊断和故障报告生成系统

DDopS团队荣获本届挑战赛季军。该团队来自中山大学计算机学院Intelligent DDS 实验室。实验室主要方向为云计算、智能运维(AIOps)、软件定义网络、分布式软件资源管理与优化、eBPF 性能监控与优化等。 选题分析 基于对竞赛数据的洞察和对时代趋势的考量&#xff0c;我们尝试应…
阅读更多...
YOLOv9改进|增加SPD-Conv无卷积步长或池化:用于低分辨率图像和小物体的新 CNN 模块

YOLOv9改进|增加SPD-Conv无卷积步长或池化:用于低分辨率图像和小物体的新 CNN 模块

专栏介绍&#xff1a;YOLOv9改进系列 | 包含深度学习最新创新&#xff0c;主力高效涨点&#xff01;&#xff01;&#xff01; 一、文章摘要 卷积神经网络(CNNs)在计算即使觉任务中如图像分类和目标检测等取得了显著的成功。然而&#xff0c;当图像分辨率较低或物体较小时&…
阅读更多...
02-设计概述

02-设计概述

上一篇&#xff1a;01-导言 本章重点讨论 JNI 中的主要设计问题。本节中的大多数设计问题都与本地方法有关。调用 API 的设计将在第 5 章&#xff1a;调用 API 中介绍。 2.1 JNI 接口函数和指针 本地代码通过调用 JNI 函数来访问 Java 虚拟机功能。JNI 函数可通过接口指针使用…
阅读更多...
基于SpringBoot的企业头条管理系统

基于SpringBoot的企业头条管理系统

文章目录 项目介绍主要功能截图&#xff1a;部分代码展示设计总结项目获取方式 &#x1f345; 作者主页&#xff1a;超级无敌暴龙战士塔塔开 &#x1f345; 简介&#xff1a;Java领域优质创作者&#x1f3c6;、 简历模板、学习资料、面试题库【关注我&#xff0c;都给你】 &…
阅读更多...
springBoot整合Redis（二、RedisTemplate操作Redis）

springBoot整合Redis（二、RedisTemplate操作Redis）

Spring-data-redis是spring大家族的一部分&#xff0c;提供了在srping应用中通过简单的配置访问redis服务&#xff0c;对reids底层开发包(Jedis, JRedis, and RJC)进行了高度封装&#xff0c;RedisTemplate提供了redis各种操作、异常处理及序列化&#xff0c;支持发布订阅&…
阅读更多...
4.6.CVAT——带点的注释详细操作

4.6.CVAT——带点的注释详细操作

文章目录 1.形状模式下的点2.单点线性插值 使用单个点或包含多个点的形状对任务进行标注的指南。 1.形状模式下的点 它用于面部、地标注释等。 在开始之前&#xff0c;您需要选择 Points .如有必要&#xff0c;您可以在 Number of points 字段中设置固定数量的点&#xff0c;…
阅读更多...
并查集（Disjoint Set）

并查集（Disjoint Set）

目录 1.定义 2.初始化 3.查找 4.合并 4.1.按秩合并&#xff08;启发式合并&#xff09; 5.例题 题目描述 输入格式 输出格式 输入输出样例 说明/提示 1.定义 并查集&#xff0c;也称为不相交集合数据结构&#xff0c;是一种用于管理元素分组以及查找元素所属组的数…
阅读更多...
Julia语言中的元编程

Julia语言中的元编程

在 Julia 语言中&#xff0c;元编程&#xff08;Metaprogramming&#xff09;可以生成或操作其他代码。这种技术允许程序员在编译时或运行时动态地创建、修改或分析代码&#xff0c;从而增强语言的功能和灵活性&#xff0c;以宏&#xff08;Macros&#xff09;、表达式和符号&a…
阅读更多...
【python报错】Intel MKL FATAL ERROR: Cannot load mkl/../../../libmkl_rt.so.2.

【python报错】Intel MKL FATAL ERROR: Cannot load mkl/../../../libmkl_rt.so.2.

python报错&#xff1a; Intel MKL FATAL ERROR: Cannot load mkl/../../../libmkl_rt.so.2.在切换旧版numpy版本的时候&#xff0c;出现了这个报错&#xff0c;表现就是将numpy切换到<1.24的版本的时候&#xff0c;只要import numpy就弹出以上报错。 尝试了网上的各种方法…
阅读更多...
【Go语言】Go语言中的流程控制

【Go语言】Go语言中的流程控制

Go语言中的流程控制 流程控制主要用于设定计算执行的顺序&#xff0c;简历程序的逻辑结果&#xff0c;Go语言的流程控制语句与其他语言类似&#xff0c;支持如下几种流程控制语句&#xff1a; 条件语句&#xff1a;用于条件判断&#xff0c;对应的关键字有if、else和else if&a…
阅读更多...
STM32-ADC一步到位学习手册

STM32-ADC一步到位学习手册

1.按部就班陈述概念 ADC 是 Analog-to-Digital Converter 的缩写&#xff0c;指的是模拟/数字转换器。它将连续变量的模拟信号转换为离散的数字信号。在 STM32 中&#xff0c;ADC 具有高达 12 位的转换精度&#xff0c;有多达 18 个测量通道&#xff0c;其中 16 个为外部通道&…
阅读更多...
搜索算法（算法竞赛、蓝桥杯）--DFS单词接龙

搜索算法（算法竞赛、蓝桥杯）--DFS单词接龙

1、B站视频链接&#xff1a;B20 DFS 单词接龙_哔哩哔哩_bilibili 题目链接&#xff1a;[NOIP2000 提高组] 单词接龙 - 洛谷 #include <bits/stdc.h> using namespace std; const int N25; int n,ans; int used[N];//每个单词的使用次数 string word[N];void dfs(string…
阅读更多...
姓名若有孤寡数，极不利婚姻！

姓名若有孤寡数，极不利婚姻！

易经云“同声相应&#xff0c;同气相求”&#xff0c;一个人的名字会形成一个磁场&#xff0c;在个人的生活当中会影响到自己的方方面面&#xff0c;如运势、事业工作、桃花运等&#xff0c;同时也会影响自己的感情婚姻哦。 峰民曾经在办公室接待了一位女士&#xff0c;看了她…
阅读更多...
备战蓝桥杯---状态压缩DP进阶题1

备战蓝桥杯---状态压缩DP进阶题1

我们来看一看一道比较难的问题&#xff08;十分十分的巧妙&#xff09;&#xff1a; 显然我们应该一行一行放&#xff0c;又竖的会对下一行产生影响&#xff0c;我们令横着放为0&#xff0c;竖着放的上方为1. 对于下一行&#xff0c;前一行放1的下面为0&#xff0c;但是会出现…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023