并查集（Disjoint Set）

news2024/9/24 17:55:58

1.定义

2.初始化

3.查找

4.合并

4.1.按秩合并（启发式合并）

5.例题

题目描述

输入格式

输出格式

输入输出样例

说明/提示

1.定义

并查集，也称为不相交集合数据结构，是一种用于管理元素分组以及查找元素所属组的数据结构。

在并查集中，每个集合通常用一棵树来表示，其中树的根节点代表集合的代表元素。通过查找操作可以找到元素所属的集合，而通过合并操作可以将两个集合合并为一个集合。

顾名思义，并查集支持两种操作：

合并（Union）：合并两个元素所属集合（合并对应的树）
查询（Find）：查询某个元素所属集合（查询对应的树的根节点），这可以用于判断两个元素是否属于同一集合

并查集在经过修改后可以支持单个元素的删除、移动；使用动态开点线段树还可以实现可持久化并查集。

注意：并查集无法以较低复杂度实现集合的分离。

2.初始化

用一个数组dsu[x]来存x的父节点。

例如：

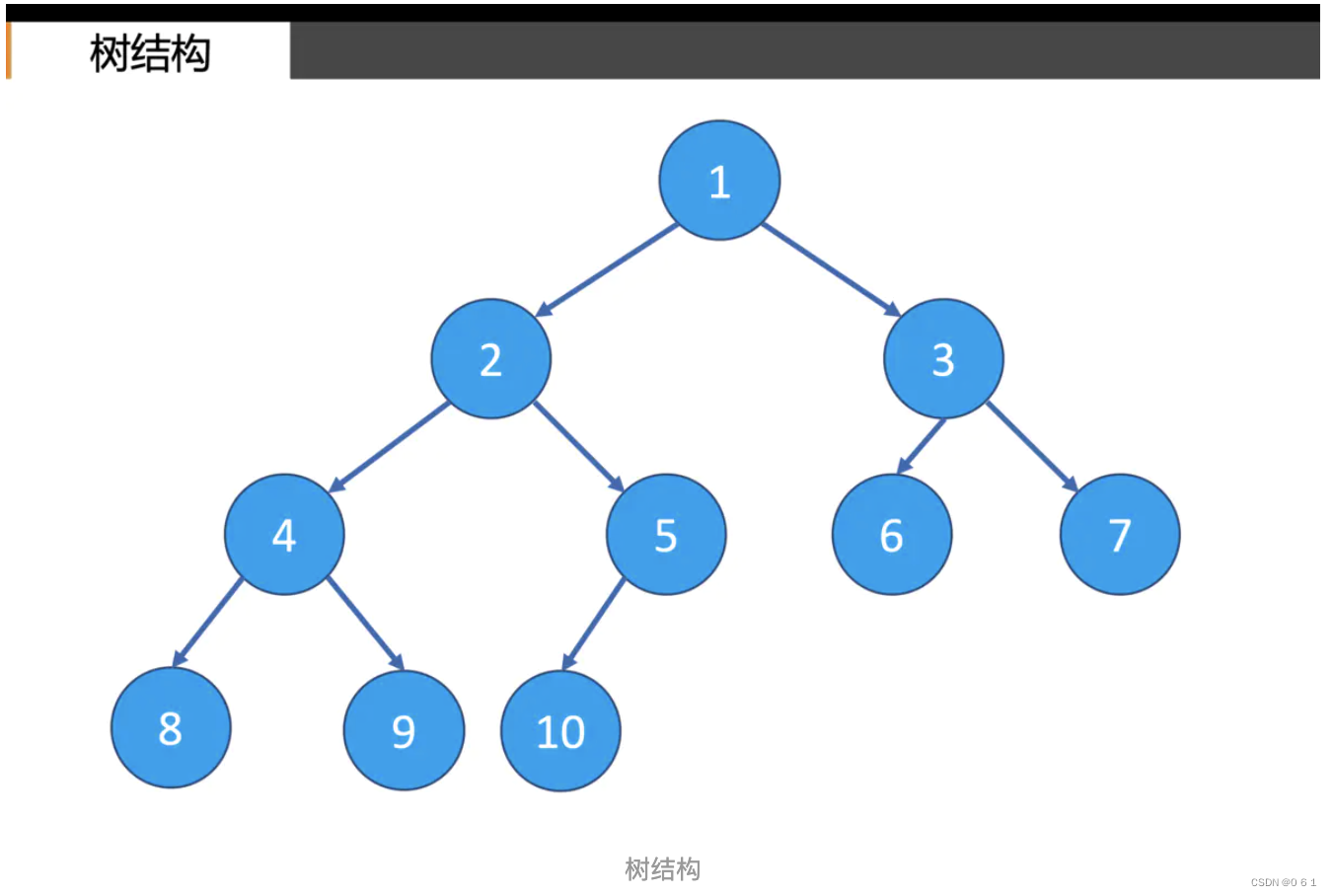
此时dsu[1] = 1，dsu[6]=3等；

初始时，每个元素都位于一个单独的集合，表示为一棵只有根节点的树，方便起见，最开始每个元素的父节点为自己。

void init(int* fa) {
	for (int i = 1; i <= N; i++)fa[i] = i;
}

3.查找

根节点时集合的代表，查找就是找到元素所在集合的根。

1.如果父节点等于自己，则找到了根并返回。
2.如果还没找到根，则继续递归查找。

int find(int x) {
	if (fa[x] == x) return x;
	return find(fa[x]);
}

如果链式很长这种查找会很耗时，我们可以在返回的同时，将fa[x]的值修改为根节点，即将各节点的父节点都修改为根节点，也叫带路径的查找（路径压缩），这样可以加快以后的查找进程。

int find(int x) {
	if (fa[x] == x) return x;
	return fa[x] = find(fa[x]);
}

4.合并

把一个集合的根节点指向另一个集合的根节点。

void unionset(int x, int y) {//将x的根节点指向y的根节点
	fa[find(x)] = find(y);
}

在并查集中，将小集合的根节点指向大集合的根节点是一种优化策略，通常结合了按秩合并的思想。这个优化策略有助于保持并查集的平衡性，避免树过深，从而提高查找和合并操作的效率。以下是这种优化策略的一些优点：

平衡性： 将小树合并到大树上可以保持并查集的平衡性。通过始终将高度较小的树合并到高度较大的树上，可以避免出现极端情况下树的高度过高，从而降低了查找操作的时间复杂度。
减小树的高度： 通过将小树合并到大树上，可以减小整个并查集中树的高度。较低的树高度意味着在进行查找操作时需要遍历的节点数量更少，提高了查找操作的效率。
降低时间复杂度： 通过维护平衡的树结构，查找和合并操作的平均时间复杂度可以更接近于O(1)，提高了整体的操作效率，减小树的高度可以减少下一次查询时的递归次数。
避免退化： 如果不进行优化，当按照树的深度进行合并时，可能会出现树的退化情况，即树的高度过高，导致操作的效率下降。

4.1.按秩合并（启发式合并）

把小集合的根节点指向大集合的根节点。

void unionset(int x, int y) {
	x = find(x);
	y = find(y);
	if (x == y)return;//在同一个集合不用合并
	if (siz[x] > siz[y])swap(x, y);//如果x的大小大于y的大小，交换，让x表示大集合，y表示小集合
	fa[x] = y;//再将x指向y
	siz[y] += siz[x];
}

算法竞赛按秩合并不常用，因为路径压缩足够好了，不用再用空间换时间。

5.例题

洛谷：P3367 【模板】并查集

题目描述

如题，现在有一个并查集，你需要完成合并和查询操作。

输入格式

第一行包含两个整数 N,M ,表示共有 N 个元素和 M 个操作。

接下来 M 行，每行包含三个整数 $Z_{i},X_{i},Y_{i}$ 。

当 $Z_{i}$ = 1 时，将 $X_{i}$ 与 $Y_{i}$ 所在的集合合并。

当 $Z_{i}$ = 2 时，输出 $X_{i}$ 与 $Y_{i}$ 是否在同一集合内，是的输出 Y ；否则输出 N 。

输出格式

对于每一个 $Z_{i}$ = 2 的操作，都有一行输出，每行包含一个大写字母，为 Y 或者 N 。

输入输出样例

输入 #1复制

输出 #1复制

N
Y
N
Y

说明/提示

对于 30% 的数据，N≤10，M≤20。

对于 70% 的数据，N≤100，M≤ $10^{3}$ 。

对于 100% 的数据，1≤N≤ $10^{4}$ ，1≤M≤2× $10^{5}$ ，1≤ $X_{i}$ , $Y_{i}$ ≤N， $Z_{i}$ ∈{1,2}。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 10001;
int fa[N];
int find(int x) {
	if (fa[x] == x) return x;
	return fa[x] = find(fa[x]);
}
void unionset(int x, int y) {
	fa[find(x)] = find(y);
}
void f(int x, int y) {
	if (find(x) == find(y))cout << "Y" << endl;
	else cout << "N" << endl;
}
void solve() {
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= n; i++) fa[i] = i;
	int z, x, y;
	while (m--) {
		cin >> z >> x >> y;
		if (z == 1) {
			unionset(x, y);
		}
		else f(x, y);
	}
}
int main() {
	ios::sync_with_stdio;
	cin.tie(0);
	cout.tie(0);
	solve();
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1483339.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！