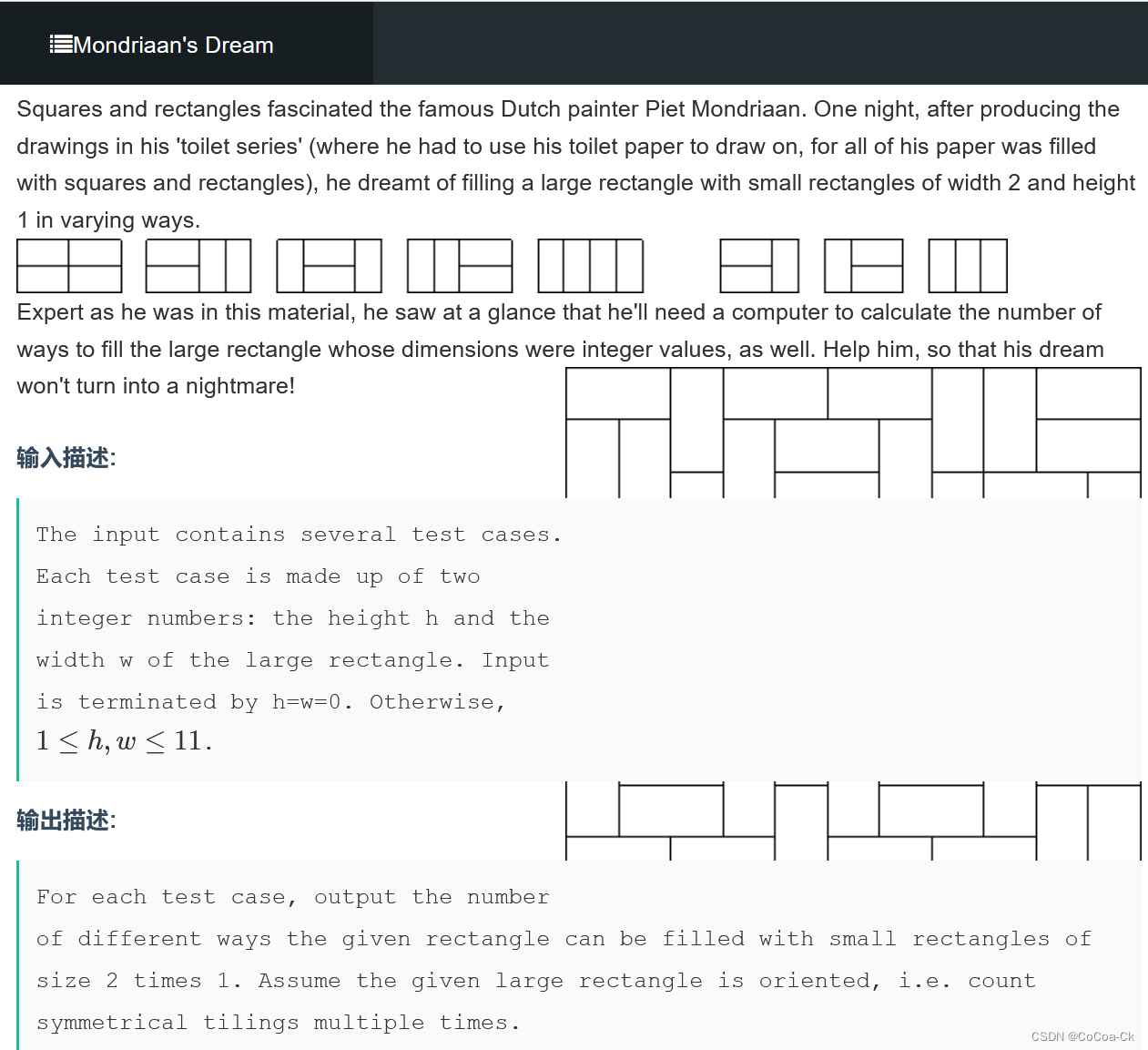
题目描述

解题思路

首先看到题目，一开始是并没有思路的。这时候可以在纸上进行演算一下结果。当只有一对括号的时候，我们可以得知结果[“()”],当有两对括号的时候，我们可以发现，括号在第一个基础上，要么在括号内部出现，要么在括号外部出现。用公式来表达就是(+p+)+q。p和q代表的是一对括号可能存在的地方。以此类推，当有n对括号的时候，假设p=i,q=n-i-1。这时候大家应该知道这题目是怎么一回事了，这时候就是需要我们实现这一个过程。首先，我们需要定义一个列表，这个列表中存放着所有的括号存在的情况，下标就代表第i个括号对对应的情况。具体如下：
首先检查输入的 n 是否为 0，如果是，则直接返回一个空列表 []，因为在这种情况下无法生成有效的括号组合。

初始化一个列表 result，用于存储不同组合情况下的括号序列。首先将空字符串 “” 和单对括号 () 分别作为 n=0 和 n=1 时的初始情况加入到 result 中。

接下来，对于 n 从 2 到输入的 n 的范围进行循环，依次生成包含 n 对括号的有效括号组合。

在每一轮循环中，通过两个嵌套的循环，分别遍历内部括号和外部括号的组合情况。对于每一对内外括号组合，将内部括号组合和外部括号组合进行组合，形成新的括号序列，并将这些新的括号序列添加到 new_combinations 列表中。

将生成的新的括号序列列表 new_combinations 添加到 result 中，以便在下一轮循环中使用。

最后，返回 result[n]，即包含 n 对括号的有效括号组合列表

代码如下

from typing import List

class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        if n == 0:
            return []

        result = []
        result.append([""])  # 初始化n=0和n=1时的情况
        result.append(["()"])

        for i in range(2, n + 1):
            new_combinations = []
            for j in range(i):
                inside = result[j]
                outside = result[i - 1 - j]
                for inside_str in inside:
                    for outside_str in outside:
                        new_combinations.append("(" + inside_str + ")" + outside_str)

            result.append(new_combinations)

        return result[n]