我们来看一看一道比较难的问题（十分十分的巧妙）：

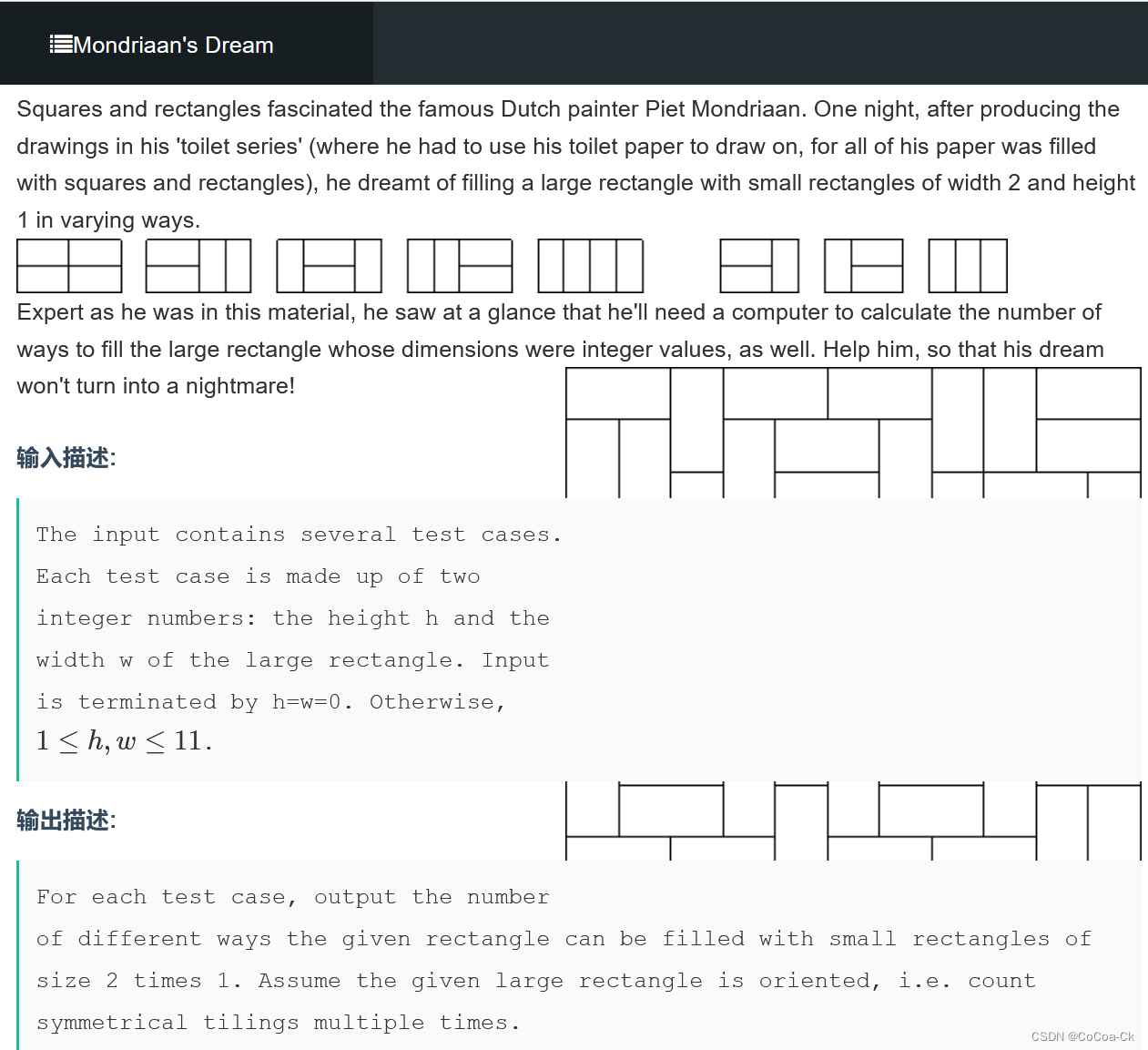
显然我们应该一行一行放，又竖的会对下一行产生影响，我们令横着放为0，竖着放的上方为1.

对于下一行，前一行放1的下面为0，但是会出现这么个情况：

10001,这3个0可能是竖着放的下方，也可以是一个横放+1个竖着放的下方，而对于000下面的一定不能是3个0，只可以是100或001或111.

综上，我们可以得到如下规则：

1.st&st'!=0是不可能的。

2.我们在忽略竖的0下不能有连续奇数的0.

显然，对于一个01矩阵，它与1种方案是一一映射的。

有了这两个规则，我们求的就是最后一行全为0的方案数。

但是，对于验证第二个规则比较麻烦，我们如何用二进制的性质来化简呢？

我们假设上一行为st1,本行为st2，我们取反st1,让他-st2，这样子我们就把竖的0忽略了。

我们只要计算是否有奇数的连续的1即可。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,m;
long long dp[15][3000];
bool lian(int x){
    int cnt=0;
    int q=m;
    while(q--){
        if(x&1) cnt++;
        else{
            if(cnt%2==1) return 1;
            cnt=0;
        }
        x>>=1;
    }
    return cnt%2;
}
int main(){
    while(cin>>n>>m){
        if(n==0&&m==0) break;
        if(n*m%2) {
            printf("0\n");
            continue;
        }
        memset(dp,0,sizeof(dp));
        for(int i=0;i<=(1<<m)-1;i++){
            if(lian((~0)-i)==1) continue;
            dp[1][i]=1;
        }
        for(int i=2;i<=n;i++){
            for(int j=0;j<=(1<<m)-1;j++){
                for(int k=0;k<=(1<<m)-1;k++){
                    if(k&j) continue;
                    if(lian((~k)-j)==1) continue;
                    dp[i][j]+=dp[i-1][k];
                }
            }
        }
        cout<<dp[n][0]<<endl;
    }
}