链式插补 (MICE)：弥合不完整数据分析的差距

news2024/9/27 7:18:37

导读

数据缺失可能会扭曲结果，降低统计功效，并且在某些情况下，导致估计有偏差，从而破坏从数据中得出的结论的可靠性。

处理缺失数据的传统方法（例如剔除或均值插补）通常会引入自己的偏差或无法充分利用数据集中的可用信息。

链式方程插补 (MICE) 的出现为解决这一普遍问题提供了一种更复杂、更灵活的方法，为研究人员提供了一种可以处理现实世界数据固有的复杂性和不确定性的工具。

数据缺失的存在类似于在隐藏地形的地图上导航。链式方程插补 (MICE) 方法充当指南针，引导研究人员穿过这些模糊的路径，确保所采取的每一步都是最佳的，得出的每一个结论都尽可能准确。

有需要的朋友关注公众号【小Z的科研日常】，获取更多内容。

01、MCIE

链式方程插补 (MICE) 是一种用于处理数据集中缺失数据的统计技术。这是一种多功能方法，可以以灵活而稳健的方式处理缺失值，使其在社会科学到生物统计学等领域广受欢迎。以下是详细概述：

1.1 关键原则

① 多重插补：与使用单个估计值填充缺失值的单一插补方法不同，MICE 会生成多重插补。这种方法通过创建几个不同的合理数据集来填充缺失值，从而承认缺失数据真实值的不确定性。

② 链式方程：MICE 通过使用一系列回归模型在逐个变量的过程中估算缺失数据来进行操作。

每个缺失数据的变量都会有条件地估算到数据集中的其他变量。该过程是“链式的”，因为它迭代地循环变量，根据上一步的更新数据更新每一步的插补。

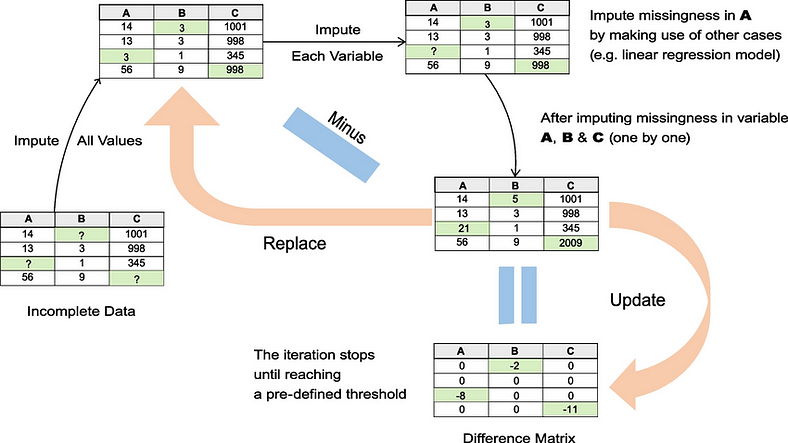
1.2 MICE如何运作？

① 初始化：缺失值最初用占位符值填充，通常是该变量观测值的平均值或中位数。

② 迭代：对于每个缺失数据的变量，使用其他变量作为预测变量，对观测值拟合回归模型。然后根据该模型估算缺失值。依次对每个变量重复此步骤，循环遍历变量进行多次迭代。

③ 收敛：经过指定次数的迭代后，假定该过程已收敛，这意味着进一步循环变量不会显着改变插补。

通常，前几次迭代作为“老化”期被丢弃，并且通过从随后的迭代中采样来创建多个估算数据集。

1.3 MICE优点

灵活性：MICE 可以处理不同类型的变量（连续、二元、分类）和不同的缺失数据机制。
稳健性：通过生成多重插补，MICE 提供了一种量化由于缺失数据而导致的不确定性的方法，而这种不确定性在单一插补方法中经常被忽视。
效率：链式方程方法允许根据最适合其分布和与其他变量关系的模型来估算每个变量。

1.4 MICE局限性

假设：MICE 假设数据随机丢失 (MAR)，但情况可能并非总是如此。如果数据不是随机丢失 (MNAR)，则插补可能会有偏差。
复杂性：迭代过程以及生成和分析多个数据集的需要可能是计算密集型的，并且需要更复杂的统计分析。

1.5 应用领域

MICE广泛应用于各个领域，在处理不完整数据集时进行数据分析。它在纵向研究、临床试验和调查中特别有用，因为丢失数据是一个常见问题。

通过提供稳健的缺失值输入方法，MICE 帮助研究人员和分析师充分利用他们的数据，从而得出更准确、更可靠的结论。

1.6 MCIE的起源

MICE 源于更广泛的多重插补框架，这是鲁宾于 1987 年提出的一个概念，旨在通过创建多个插补数据集、单独分析每个数据集，然后组合结果来解决因缺失数据而造成的不确定性。

MICE 在此基础上构建，通过在链式迭代过程中采用一系列回归模型来生成这些多重插补。这种方法创新使得能够以更大的灵活性和准确性解决从健康科学到经济学等不同领域的各种缺失数据问题。

1.7 MCIE的机制

MICE 的核心是通过迭代过程进行操作，其中每个缺失数据的变量都按顺序进行估算，并使用其他变量作为预测变量。

该过程从初步插补阶段开始，其中缺失值由初始估计值填充，例如观测值的平均值或中位数。在连续迭代中，对于每个缺失数据的变量，将回归模型拟合到观察到的数据，同时考虑所有其他变量的当前插补。

然后根据该模型的预测分布估算缺失值。这个循环在一系列迭代中重复，使得插补随着模型调整到反馈循环中的插补值而演变。

1.8 MCIE的优势与创新

与传统插补方法相比，MICE 方法具有多种优势。

首先也是最重要的是它的灵活性：通过为每个变量选择适当的模型，MICE 可以容纳从连续到分类的不同类型和分布的变量。如果数据随机丢失 (MAR) 的假设成立，这种适应性可以扩展到处理各种丢失模式和机制。

此外，通过生成多重插补，MICE 承认并量化插补过程中固有的不确定性，从而实现更稳健的统计推断。

02、代码

为了演示在 Python 中使用链式方程插补 (MICE)，我们将创建一个包含缺失值的合成数据集，应用 MICE 插补这些值，然后使用指标和图评估插补质量。

我们将使用该pandas库来处理数据、numpy生成缺失值、sklearn创建合成数据集和评估指标以及matplotlib绘图seaborn。

我们还将使用IterativeImputerfrom，sklearn.impute因为它实现了类似 MICE 的方法。

import numpy as np
import pandas as pd
from sklearn.datasets import make_regression
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
import seaborn as sns

# 生成合成数据集
X, y = make_regression(n_samples=1000, n_features=10, noise=0.1, random_state=42)

# 转换为 DataFrame，以便于操作
df = pd.DataFrame(X, columns=[f'Feature_{i}' for i in range(X.shape[1])])
df['Target'] = y

# 显示前几行
df.head()

# I引入缺失值
np.random.seed(42)
df_missing = df.mask(np.random.random(df.shape) < 0.1)

# 显示前几行以验证缺失值
df_missing.head()

# 初始化 MICE 计算器
mice_imputer = IterativeImputer(max_iter=10, random_state=42)

# 拟合和转换数据集以填补缺失值
df_imputed = mice_imputer.fit_transform(df_missing)

# 将拟合数据转换回 pandas DataFrame
df_imputed = pd.DataFrame(df_imputed, columns=df.columns)
df_imputed.head()

# 计算每个特征的 RMSE
rmse = np.sqrt(mean_squared_error(df, df_imputed, multioutput='raw_values'))

# 打印每个特征的均方根误差
print(f'RMSE for each feature: {rmse}')

# 选择要绘制的特征
feature_to_plot = 'Feature_0'

# 绘制原始分布图和处理后的分布图
plt.figure(figsize=(10, 6))
sns.kdeplot(df[feature_to_plot], label='Original', color='green', linestyle="--")
sns.kdeplot(df_imputed[feature_to_plot], label='Imputed', color='red', linestyle="-")
plt.legend()
plt.title(f'Distribution of Original vs. Imputed Values for {feature_to_plot}')
plt.xlabel('Value')
plt.ylabel('Density')
plt.show()

输出：

RMSE for each feature: [ 0.24095716  0.22593846  0.21704334  0.15838514  0.25103187  0.29992605
  0.1432319   0.22131897  0.27775888  0.16266519 15.56987127]