引入:RMQ问题:
什么是RMQ?

显然,我们无法用前缀维护,因此,我们需要用到线段树的知识:
什么是线段树?
线段树是用一种树状结构存储一个连续区间信息的数据结构
下面我们用图解释用它来查询2--5信息的方式:
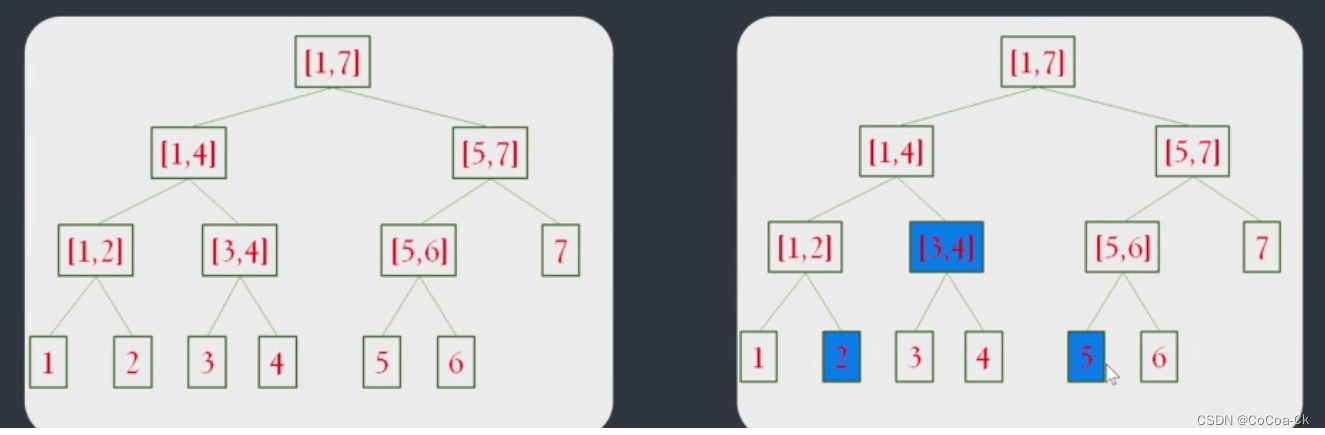
由此,我们可以得到几点性质:
1.他是一个平衡的二叉树。
2.对于任意两个节点,要么完全包含,要么互不相交。
3.任意的线段[a,b]在查询过程中最多分为log(b-a)个。
4.除建树外为logn.
我们来一道模板题试试水:

下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,a[100000];
int tree[4*100000];
void build(int p,int l,int r){
if(l==r){
tree[p]=a[l];
return;
}
int mid=(l+r)/2;
build(p*2,l,mid);
build(p*2+1,mid+1,r);
tree[p]=tree[p*2+1]+tree[p*2];
return;
}
void change(int p,int l,int r,int pos,int num){
if(l==r){
tree[p]+=num;
return;
}
int mid=(l+r)/2;
if(pos<=mid) change(p*2,l,mid,pos,num);
else change(p*2+1,mid+1,r,pos,num);
tree[p]=tree[2*p]+tree[2*p+1];
return;
}
int calc(int p,int l,int r,int x,int y){
if(l>=x&&r<=y){
return tree[p];
}
int mid=(l+r)/2;
if(y<=mid) return calc(p*2,l,mid,x,y);
if(x>mid) return calc(p*2+1,mid+1,r,x,y);
return calc(p*2,l,mid,x,mid)+calc(p*2+1,mid+1,r,mid+1,y);
}
int main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);
for(int i=1;i<=n;i++){
int x,y,z;
cin>>x>>y>>z;
if(x==1){
change(1,1,n,y,z);
}
else cout<<calc(1,1,n,y,z);
}
} 让我们来看看它的实际应用吧:
区间和问题之懒标记:

我们维护一下节点的两个信息:
1.sum[i]第i个节点对应的区间和。
2.add[i]第i个节点对应区间整体加上的值并且没有同步给儿子。
这里我们就知道了为什么叫lazy,该标记仅当被标记的区间有部分被更改才顺路把标记下放给它的儿子。这样就可以减少修改的次数了。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,a[100010],m;
int tree[4*100010];
int lazy[4*100010];
void build(int p,int l,int r){//建树
if(l==r){
tree[p]=a[l];
return;
}
int mid=(l+r)/2;
build(p*2,l,mid);
build(p*2+1,mid+1,r);
tree[p]=tree[p*2+1]+tree[p*2];
return;
}
void pushdown(int p,int l,int r){//lazy标记下移
int mid=(l+r)/2;
lazy[p*2]+=lazy[p];
lazy[p*2+1]+=lazy[p];
tree[p*2]+=lazy[p]*(mid-l+1);//更新子节点的值
tree[p*2+1]+=lazy[p]*(r-mid);
lazy[p]=0;//自己因为下移清0
}
void change(int p,int l,int r,int x,int y,int num){
if(x<=l&&r<=y){
tree[p]+=num*(r-l+1);
lazy[p]+=num;
return;
}
if(lazy[p]!=0){//区间部分修改,需要下移
pushdown(p,l,r);
}
int mid=(l+r)/2;
if(y<=mid) change(p*2,l,mid,x,y,num);
if(x>mid) change(p*2+1,mid+1,r,x,y,num);
if(x<=mid&&y>mid){
change(p*2,l,mid,x,mid,num);
change(p*2+1,mid+1,r,mid+1,y,num);}
tree[p]=tree[2*p]+tree[2*p+1];
return;
}
int calc(int p,int l,int r,int x,int y){
if(l>=x&&r<=y){
return tree[p];
}
if(lazy[p]!=0){
pushdown(p,l,r);
}
int mid=(l+r)/2;
if(y<=mid) return calc(p*2,l,mid,x,y);
if(x>mid) return calc(p*2+1,mid+1,r,x,y);
return calc(p*2,l,mid,x,mid)+calc(p*2+1,mid+1,r,mid+1,y);
}
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
build(1,1,n);
for(int i=1;i<=m;i++){
int x,y,k,op;
scanf("%lld%lld%lld",&op,&x,&y);
if(op==1){
scanf("%lld",&k);
change(1,1,n,x,y,k);
}
else cout<<calc(1,1,n,x,y)<<endl;
}
} 区间平方和问题:

我们还是用lazy标记,不过这时我们维护的sum应该是平方和。那么我们如何维护呢?
因此我们只要维护ai的前缀和即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,a[100010],m,sum[4*100010];
int tree[4*100010];
int lazy[4*100010];
void pushdown(int p,int l,int r);
int calc(int p,int l,int r,int x,int y,int k);
void build(int p,int l,int r){//建树
if(l==r){
tree[p]=a[l]*a[l];
sum[p]=a[l];
return;
}
int mid=(l+r)/2;
build(p*2,l,mid);
build(p*2+1,mid+1,r);
tree[p]=tree[p*2+1]+tree[p*2];
sum[p]=sum[p*2+1]+sum[p*2+1];
return;
}
void pushdown(int p,int l,int r){//lazy标记下移
int mid=(l+r)/2;
lazy[p*2]+=lazy[p];
lazy[p*2+1]+=lazy[p];
tree[p*2]+=2*lazy[p]*(sum[2*p])+lazy[p]*lazy[p]*(mid-l+1);//更新子节点的值
tree[p*2+1]+=2*lazy[p]*(sum[2*p+1])+lazy[p]*lazy[p]*(r-mid);
sum[p*2]+=lazy[p]*(mid-l+1);
sum[p*2+1]+=lazy[p]*(r-mid);
lazy[p]=0;//自己因为下移清0
}
void change(int p,int l,int r,int x,int y,int num){
if(x<=l&&r<=y){
tree[p]+=2*num*(sum[p])+num*num*(r-l+1);
sum[p]+=num*(r-l+1);
lazy[p]+=num;
return;
}
if(lazy[p]!=0){//区间部分修改,需要下移
pushdown(p,l,r);
}
int mid=(l+r)/2;
if(y<=mid) change(p*2,l,mid,x,y,num);
if(x>mid) change(p*2+1,mid+1,r,x,y,num);
if(x<=mid&&y>mid){
change(p*2,l,mid,x,mid,num);
change(p*2+1,mid+1,r,mid+1,y,num);}
tree[p]=tree[2*p]+tree[2*p+1];
sum[p]=sum[2*p]+sum[2*p+1];
return;
}
int calc(int p,int l,int r,int x,int y,int k){
if(l>=x&&r<=y){
if(k==1) return tree[p];
else return sum[p];
}
if(lazy[p]!=0){
pushdown(p,l,r);
}
int mid=(l+r)/2;
if(y<=mid) return calc(p*2,l,mid,x,y,k);
if(x>mid) return calc(p*2+1,mid+1,r,x,y,k);
return calc(p*2,l,mid,x,mid,k)+calc(p*2+1,mid+1,r,mid+1,y,k);
}
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
build(1,1,n);
for(int i=1;i<=m;i++){
int x,y,k,op;
scanf("%lld%lld%lld",&op,&x,&y);
if(op==1){
scanf("%lld",&k);
change(1,1,n,x,y,k);
}
else cout<<calc(1,1,n,x,y,1)<<endl;
}
}