图像变换是对图像信息进行变换，是能量保持但重新分配，利于加工处理。这里主要介绍傅里叶变换的图像频域滤波。

  

  图像从空间域变换到频域后，其低频分量对应图像中灰度值变化较为缓慢的区域，高频分量表征图像中物体的边缘和随机噪声等信息。

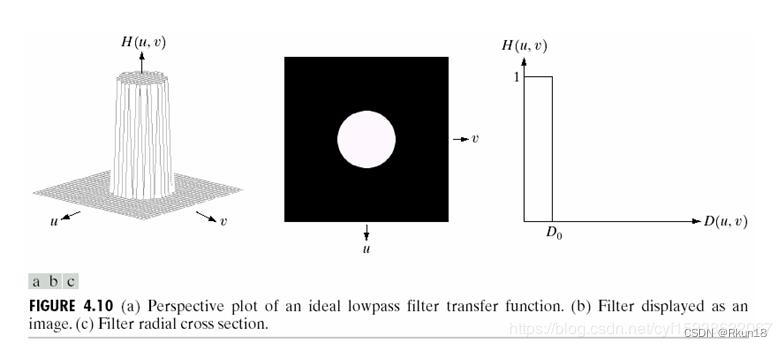
  低通滤波是指保留低频分量，而通过滤波器函数H(u,v)减弱或抑制高频分量在频域进行的滤波。可以消除图像中随机噪声，减弱边缘效应，起到平滑图像的作用。

    阶段频率是一个非负整数，D(u,v)是点（u，v）到频率平面原点的距离，既。理想低通滤波器的含义是小于小于截断频率，即在半径圆之内的频率分量可以完全无损的通过，而大于阶段频率的分量被滤除。理想低通滤波器平滑作用很明显，但由于变换有一个陡峭的波形，它的逆变换有强烈的振铃效果，使得滤波后的图像产生模糊效果。

 

中文显示函数：

def set_ch():
    from pylab import mpl
    mpl.rcParams['font.sans-serif'] = ['FangSong']
    mpl.rcParams['axes.unicode_minus'] = False


set_ch()

实现低通滤波：

import numpy as np

from skimage import io
import matplotlib.pyplot as plt
from skimage.color import rgb2gray


# 设置中文
def set_ch():
    from pylab import mpl
    mpl.rcParams['font.sans-serif'] = ['FangSong']
    mpl.rcParams['axes.unicode_minus'] = False


set_ch()

D = 25
# 读入图像
Img = io.imread('I.jpg')
I = rgb2gray(Img)
# 傅里叶变换
f1 = np.fft.fft2(I)
f1_shift = np.fft.fftshift(f1)
# fftshift实现平移，让直流分量输出图像重心
# 理想低通滤波
rows, cols = I.shape
crow, ccol = int(rows / 2), int(cols / 2)  # 计算频谱中心
mask = np.zeros((rows, cols), np.uint8)
for i in range(rows):
    for j in range(cols):  # 将频谱中心小于D部分低通信息设为1，属于低通滤波
        mask[crow - D:crow + D, ccol - D:ccol + D] = 1
f1_shift = f1_shift * mask
# 傅里叶逆变换
f_ishift = np.fft.ifftshift(f1_shift)
I_back = np.fft.ifft2(f_ishift)
I_back = np.abs(I_back)
I_back = (I_back - np.amin(I_back)) / (np.amax(I_back) - np.amin(I_back))
plt.figure()
plt.subplot(121)
plt.imshow(I, cmap='gray')
plt.title("原图")
plt.subplot(122)
plt.imshow(I_back, cmap='gray')
plt.title("滤波后的图像")
plt.show()

I_back = (I_back - np.amin(I_back)) / (np.amax(I_back) - np.amin(I_back))

这一句的作用是将反演得到的图像矩阵I_back的像素值缩放到0~1之间。

首先，(I_back-np.amin(I_back))将I_back的每个像素值减去最小像素值，这样可以使得I_back的最小像素值为0。

然后，(np.amax(I_back)-np.amin(I_back))是I_back的最大像素值减去最小像素值，这样得到的值就是I_back的像素值的数值范围，即最大值与最小值之差。

最后，将I_back的每个像素值除以像素值的数值范围，就可以将I_back的像素值缩放到0~1之间。

 在上述代码后追加上直方图：

plt.figure()
plt.subplot(121)
arr=I.flatten()
plt.axis([0,1,0,20000])
plt.hist(arr, bins=256, edgecolor='None', facecolor='red')
plt.title("原图")
plt.subplot(122)
arr1=I_back.flatten()
plt.axis([0,1,0,20000])
plt.hist(arr1, bins=256, edgecolor='None', facecolor='red')
plt.title("滤波后的图像")
plt.show()

观察发现部分频率较高的灰度值被滤除，但产生了些许杂质。