---

前言

学习一下： 中心损失函数，用于用于深度人脸识别的特征判别方法
论文：https://ydwen.github.io/papers/WenECCV16.pdf
github代码：https://github.com/KaiyangZhou/pytorch-center-loss

参考：史上最全MNIST系列（三）——Centerloss在MNIST上的Pytorch实现（可视化）

---

问题引出

open-set问题

open-set 问题是一种模式识别中的问题，它指的是当训练集和测试集的类别不完全相同的情况。例如，如果训练集只包含 0 到 9 的数字，而测试集包含了 A 到 Z 的字母，那么就是一个 open-set 问题。这种情况下，分类器不仅要正确识别已知的类别，还要能够拒绝未知的类别，即将它们标记为 unknown 或 outlier。（后来我想这就是一个聚类问题）

open-set 问题与 closed-set 问题相对应，closed-set 问题是指训练集和测试集的类别完全相同的情况。例如，如果训练集和测试集都只包含 0 到 9 的数字，那么就是一个 closed-set 问题。这种情况下，分类器只需要正确识别已知的类别即可。

抛出

当我们要预测的人脸不在训练集中出现过时，我们需要让它不识别出，而不要因为与训练过的人脸相像而误判。

对于常见的图像分类问题，我们常常用softmax loss来求损失。以MNIST数据集为例，如果你的损失采用softmax loss，那么最后各个类别学出来的特征分布大概如下图：（在倒数第二层全连接层输出了一个2维的特征向量）

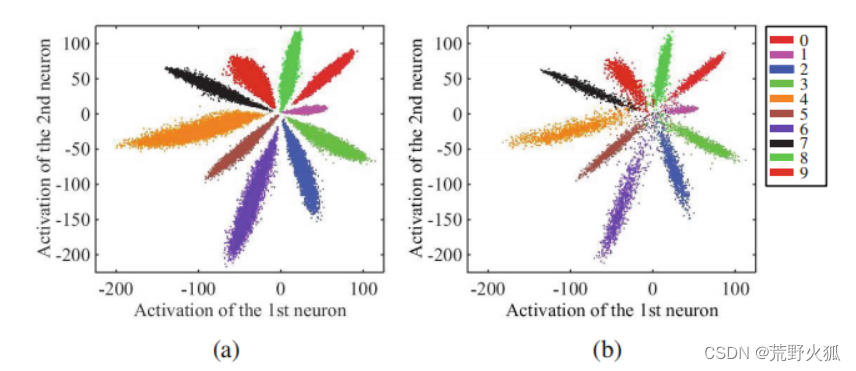
左图为训练集，右图为测试集，发现结果分类还算不错，但是每一类的界限太过模糊，若从中再加一列，则有可能出现误判。

解决方法

softmax函数、softmax-loss函数

已知softmax的函数为：

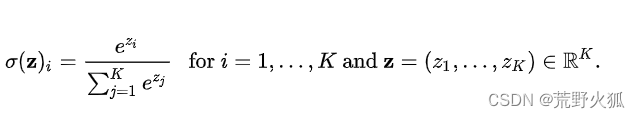
在深度学习的分类问题上，意为对应类的概率（符合每个类的概率相加和为1且0<每个类的概率<1）。（输出层后的结果）
其中 zi​ 是第 i 个输出节点的值，K是输出节点的个数，即分类的类别数。softmax函数的作用是将输出节点的值归一化为范围在 [0, 1] 且和为 1 的概率值，表示属于每个类别的可能性。

softmax的损失函数：（具体详见：一文详解Softmax函数）
在softmax的函数的基础上，我们要求正确对应类的概率最大，

即，损失函数为：(越小越好)

其中z = w^Tx+b，m是小批量的样本的个数，n是类别个数，w是全连接层的权重，b为偏置项，（一般来说w,b是要学习出来的），xi是第i个深层特征，属于第yi类。

解决

在分类的基础上，我们还要求，每个类，往自己的中心的特征靠拢，使类内间距减少，这样才能更加显出差别。

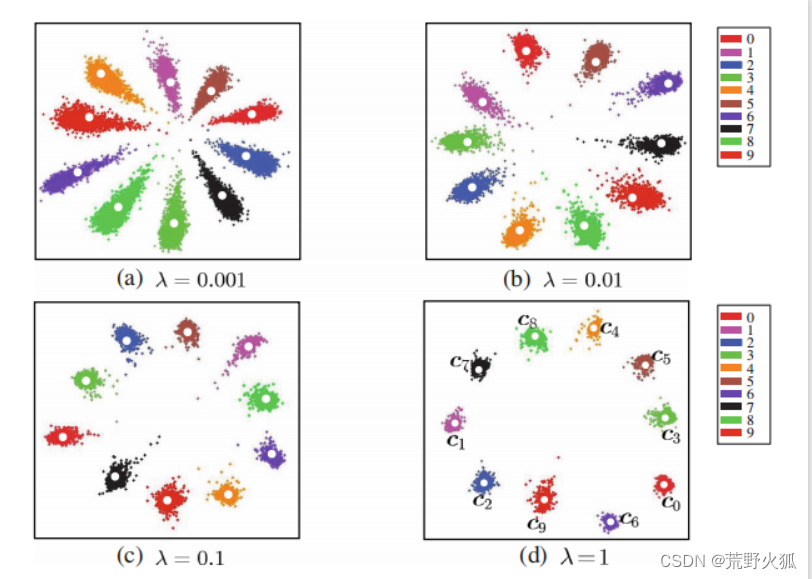
于是，论文作者提出如下新的损失函数：

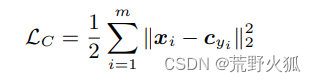
其中 xi​ 是第 i 个样本的特征向量，cyi​​ 是第 yi​ 个类别的中心向量，m 是样本的个数。
小的注意点：这里用的是样本数，也就是说，是在小批量分类任务完成后再进行的聚类任务

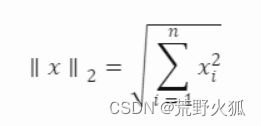
我们不难发现，作者这里用的是欧式距离的平方，即在多维空间上的两点之间真实距离的平方。
实际上，我们很容易发现，这实际上是一个聚类问题，常见的聚类问题上用的是误差平方和（SSE）损失函数：

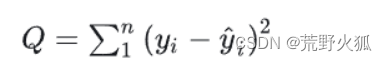
论文作者仅从此推出的欧式距离的平方，仅从形式上十分相像，当然可以作为此聚类问题的解决。

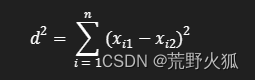
（在二维上，可以简单看成是直角三角形斜边的平方=两直角边平方和）
为何要加以平方：欧式距离的平方相比欧式距离有一些优点，例如：
1、计算更快，省去了开方的运算。
2、更加敏感，能够放大距离的差异，使得离群点更容易被发现。
3、更加方便，能够与其他平方项相结合，如方差、协方差等。

最后，作者沿用softmax损失函数与中心损失函数相加的方法（在损失函数上很常见），

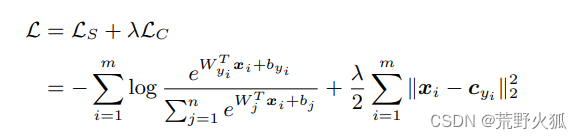
这里的1/2很容易想到是作为梯度下降时与后面的平方用来抵消的项，这里λ 可以看作调节两者损失函数的比例

来作为总体的损失函数，作为此问题的解决。

代码（center_loss.py）

原理

首先确定三个事实：
1、在之前的学习中通过实践得知（最小二乘法那块），在拟合的最后结果上，在利用SSE损失函数与MSE损失函数作为损失值参与到程序中时，拟合出的结果并无差别，只有在结果出来后，作为评判模型的好坏时，才有数值上的差别。（两者区别在于是否求平均）。
2、1/2的乘或不乘，只对运算的过程的简便程度有影响，与结果无影响。
3、图像是二维的。

于是我们将作者的的中心损失函数稍加变形。就得到了如下形式（事实上，github上给出的代码就是这么写的）

程序解释

参考：Center loss-pytorch代码详解
这里只做补充：

import torch
import torch.nn as nn

class CenterLoss(nn.Module):
    """Center loss.
    # 参考
    Reference:
    Wen et al. A Discriminative Feature Learning Approach for Deep Face Recognition. ECCV 2016.
    # 参数
    Args:
        num_classes (int): number of classes. # 类别数
        feat_dim (int): feature dimension.  # 特征维度
    """
    # 初始化        默认参数：类别数为10 特征维度为2 使用GPU
    def __init__(self, num_classes=10, feat_dim=2, use_gpu=True):
        super(CenterLoss, self).__init__() # 继承父类的所有属性
        self.num_classes = num_classes 
        self.feat_dim = feat_dim
        self.use_gpu = use_gpu

        if self.use_gpu: # 如果使用GPU
            #nn.Parameter()将一个不可训练的tensor转换成可以训练的类型parameter，并将这个parameter绑定到一个module里面,参与到模型的训练和优化中。
            #nn.Parameter的对象的requires_grad属性的默认值是True，即是可被训练的，这与torth.Tensor对象的默认值相反。
            self.centers = nn.Parameter(torch.randn(self.num_classes, self.feat_dim).cuda()) 
            # 初始化中心矩阵 .cuda()表示将数据放到GPU上
        else:
            self.centers = nn.Parameter(torch.randn(self.num_classes, self.feat_dim))

    def forward(self, x, labels): # 前向传播
        """
        Args:
            x: feature matrix with shape (batch_size, feat_dim). # 特征矩阵
            labels: ground truth labels with shape (batch_size). # 真实标签
        """
        batch_size = x.size(0) #batch_size x的形式为tensor张量
        # .pow对x中的每一个元素求平方 dim=1表示按行求和 keepdim=True表示保持原来的维度 expand是扩展维度
        distmat = torch.pow(x, 2).sum(dim=1, keepdim=True).expand(batch_size, self.num_classes) + \
                  torch.pow(self.centers, 2).sum(dim=1, keepdim=True).expand(self.num_classes, batch_size).t() #.t()表示转置 均转成batch_size x num_classes的形式
        # .addmm_()表示进行1*distmat + (-2)*x@self.centers.t()的运算    @表示矩阵乘法
        distmat.addmm_(1, -2, x, self.centers.t())

        classes = torch.arange(self.num_classes).long()# 生成一个从0到num_classes-1的整数序列 long表示数据类型
        if self.use_gpu: classes = classes.cuda() 
        #这里 .unsqueeze(0) 例[0,4,2] -> [[0,4,2]]  .unsqueeze(1) 例[0,4,2] -> [[0],[4],[2]] 
        labels = labels.unsqueeze(1).expand(batch_size, self.num_classes)# .unsqueeze(1)表示在第1维增加一个维度  .expand()表示扩展维度
        mask = labels.eq(classes.expand(batch_size, self.num_classes)) #eq是比较两个tensor是否相等，相等返回1，不相等返回0
        # *表示对应元素相乘
        dist = distmat * mask.float() # mask.float()将mask转换为float类型
        loss = dist.clamp(min=1e-12, max=1e+12).sum() / batch_size # clamp表示将dist中的元素限制在1e-12和1e+12之间

        return loss

代码运用

import torch
import torch.nn as nn
from center_loss import CenterLoss

criterion_cent =CenterLoss(10, 2,False) #10个类别，2维
torch.manual_seed(0) #设置随机种子
x = torch.randn(10, 2) # (32, 2) #32个样本，每个样本2维
labels = torch.randint(0, 10, (10,)) # (32,) #32个样本，每个样本一个标签
print(x)
print(labels)
print(criterion_cent(x, labels))

结果：

tensor([[-1.1258, -1.1524],
        [-0.2506, -0.4339],
        [ 0.5988, -1.5551],
        [-0.3414,  1.8530],
        [ 0.4681, -0.1577],
        [ 1.4437,  0.2660],
        [ 1.3894,  1.5863],
        [ 0.9463, -0.8437],
        [ 0.9318,  1.2590],
        [ 2.0050,  0.0537]])
tensor([2, 9, 1, 8, 8, 3, 6, 9, 1, 7])
tensor(2.9281, grad_fn=<DivBackward0>)

如何梯度更新

首先了解一下基本的梯度下降算法

【点云、图像】学习中 常见的数学知识及其中的关系与python实战
里的小标题：基于迭代的梯度下降算法，了解到超参数（人为设定的参数）：
学习率，w,b等。此算法为拟合出一条线。

伪代码：
1、未达到设定迭代次数
2、迭代次数epoch+1
3、计算损失值
4、计算梯度
5、更新w、b
6、达到迭代次数，结束

然后

看下这里的更新方法

其中，卷积层中初始化的参数 θc，超参数 ：λ、α 和学习率 μ ，迭代次数 t 。（λ、α、 μ均可调）
伪代码：
1、当未收敛时：
2、迭代次数t+1
3、计算损失函数 L=Ls+Lc
4、计算反向传播误差（即梯度）
5、更新w
6、更新cj
7、更新θc
8、结束

其中

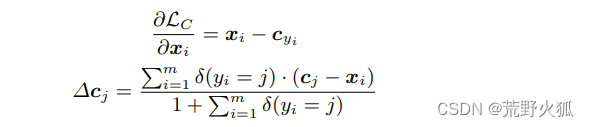
其中，如果满足条件，则 δ（条件） = 1，如果不满足，则 δ（条件） = 0。

首先：第一个公式不用多说，为中心损失函数对特征xi求偏导，即求梯度。
其次：第二个公式：加入了判断，当条件满足时（即yi=j,即就是在同一类时）Δcj=cj-xi 的小批量的所有和/m+1。相当于累加了误差求平均，以此来作为梯度。
当条件不满足时，即Δcj =0，此时这个分母的+1的作用就体现出来了，分母不能为0嘛。

补充：
第5步后面一个等号成立是因为Lc中没有W项，所以Lc对W的求导为0
第7步也是一样，求梯度，只是写成了求导的链式法则。

补充：外围知识

模型