操作环境:
MATLAB 2022a
1、算法描述
基于子空间方法的信道盲估计是一种在通信领域中广泛使用的技术,用于在不直接知道发送信号的情况下估计通信信道的特性。这种方法的核心思想是通过接收到的信号来分析信号空间的结构,从而推断出信道的特性。下面将详细介绍子空间方法的原理、实现步骤、优缺点及其在实际应用中的表现。
一、子空间方法的基本原理
子空间方法的基本原理是将接收信号的空间分解为信号子空间和噪声子空间。信号子空间包含了由于信道传播引入的信号结构信息,而噪声子空间则包含了信号中的噪声成分。通过区分这两个子空间,可以提取出信道的信息而不需要知道发送信号的具体信息。
-
信号模型的介绍:详细描述在子空间方法中使用的信号模型,包括信号、噪声以及它们如何与信道特性相互作用。可以通过数学模型来表达信号接收模型,例如使用线性代数表达信道矩阵和信号向量的关系。
-
子空间的数学定义:解释什么是信号子空间以及噪声子空间,并讨论它们在信号处理中的重要性。通过数学公式来定义这两个空间,并解释它们如何从接收到的信号中被识别和区分出来。
-
子空间分离的理论基础:深入探讨如何通过数学手段(如特征值分解)来实现信号子空间和噪声子空间的分离,以及这种分离对信道估计的意义。
二、子空间方法的关键步骤
-
接收信号的采集与建模:首先,需要收集由信道传输并由接收器接收到的信号。这些信号通常包含了由信道特性、发送信号以及噪声共同作用的结果。
-
构建数据协方差矩阵:通过接收到的信号构建数据协方差矩阵。该矩阵反映了接收信号的统计特性,是分析信号子空间和噪声子空间的基础。
-
进行奇异值分解(SVD)或特征值分解(EVD):对数据协方差矩阵进行奇异值分解或特征值分解,从而获得信号的特征向量和特征值。特征向量和特征值分别代表了信号空间的方向和能量分布。
-
子空间的分离:根据特征值的大小将特征向量分为信号子空间和噪声子空间。大的特征值对应的特征向量构成信号子空间,而小的特征值对应的特征向量构成噪声子空间。
-
信道参数的估计:最后,利用信号子空间中的信息来估计信道的参数。这可以通过多种方法实现,如最小二乘法、最大似然估计等。
三、子空间方法的优缺点
优点:
- 无需先验知识:子空间方法不需要知道发送信号的具体信息,使其非常适合于盲估计的场景。
- 鲁棒性高:相比于基于模型的方法,子空间方法对信号模型的假设较少,因此更加鲁棒。
- 适用范围广:可以应用于多种类型的信道和信号模型。
缺点:
- 计算复杂度高:特别是在进行奇异值分解或特征值分解时,计算量较大。
- 性能依赖于信噪比:在低信噪比的情况下,信号子空间和噪声子空间可能难以准确区分,影响估计性能。
四、实际应用中的表现
在实际应用中,基于子空间方法的信道盲估计已被广泛应用于无线通信、雷达信号处理、声音信号处理等领域。特别是在无线通信领域,由于无线环境的复杂性和多变性,传统的基于已知信号的信道估计方法往往难以适用。子空间方法以其不需要先验信号信息的优点,成为了一种重要的信道估计手段。
-
无线通信中的应用:通过具体的无线通信系统案例(如LTE或5G),详细分析子空间方法如何用于信道估计,包括实际操作的步骤、遇到的挑战和解决方案。
-
雷达信号处理的应用:探讨子空间方法在雷达信号处理中的应用,包括目标检测、定位以及速度估计等方面的应用实例。
-
声音信号处理的应用:分析子空间方法在声音信号处理,特别是在回声消除、噪声抑制等方面的应用,以及实现这些应用时的具体技术和策略。
五、总结
基于子空间方法的信道盲估计是一种强大的信道估计技术,它通过分析接收信号的空间结构来估计信道特性。尽管存在计算复杂度高和在低信噪比下性能可能下降的问题,但其在多个领域内的广泛应用证明了其有效性和实用性。随着计算能力的提高和算法的优化,预计子空间方法在信道估计领域的应用将会更加广泛和深入。
2、仿真结果演示
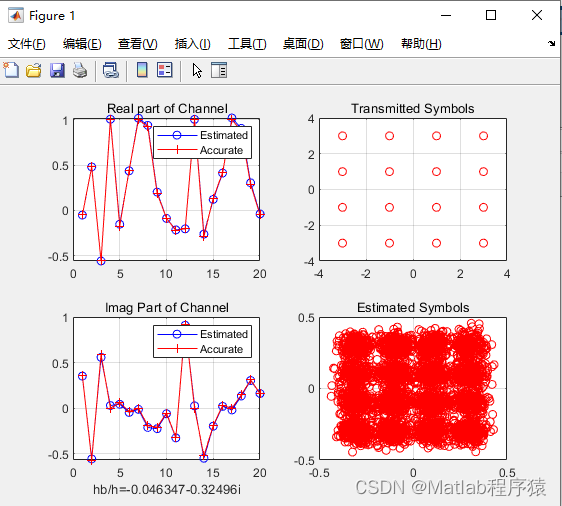
3、关键代码展示
略
4、MATLAB 源码获取
V
点击下方名片