目录
插入排序:
核心思想:
时间复杂度:
冒泡排序:
核心思想:
时间复杂度:
希尔排序:
核心思想:
时间复杂度:
选择排序:
核心思想:
时间复杂度:
堆排序:
核心思想:
时间复杂度:
快速排序:
霍尔版本:
核心思想:
快速排序小区间优化:
快速单趟排序改进思路1:挖坑法
快速单趟排序改进思路2:前后指针法
非递归快速排序:
所有排序的源码:
头文件
实现文件:
测试文件:
插入排序:
核心思想:
前面的数据有序,再将后一个数据插入前面的数据,就是一直保证前面的是有序的
例如:前1个有序、前2个有序、前3个有序、塞纳4个有序。。。以此类推,最后n个数据全部有序
在已经排序好的系序列内插入值
先单趟,再多趟
使用顺序表第一个位置记录数据个数很不好,例如哨兵的设计,因为数据的个数和数据的类型不一致,假设数据类型是char
设计数据结构不要感觉,如果感觉可以,那么可以的理由是什么;如果感觉不可以,那么不可以的理由是什么,不可以似是而非
要有具体的理由,而不是空凭感觉,有充分的理由,据具体的分析,好为什么好?有理有据
该种算法在顺序有序或者接近有序效率比较高,但是逆序效果就会非常差,注意,这个特点很重要
写排序算法,先单趟控制,不要一来直接整体控制,比较复杂,不好把握
时间复杂度:
最坏O(n^2)
最好O(n)
冒泡排序:
核心思想:
每一趟都保证将最大的数据放到最后一个位置
每一次两两比较,(升序)前一个比后一个大,交换位置,再比较后两个数据,前一个比后一个大,再交换
在第一躺的交换就将所有的数据进行了一次遍历比较,保证了将最大的数据放到最后面
再在此基础上进行第二躺的比较,目的在于将第二大的数据放到最后的位置
对于冒泡排序和插入排序的区别:
冒牌排序无论是有序、乱序还是逆序,都是严格的等差数列
但是对于插入排序来说,除非是最坏的情况,基本都难以达到等差数列的量级,因为中间的交换次数会少于最多的次数
时间复杂度:
都是O(n^2)
希尔排序:
核心思想:
1、预排序(接近有序):核心思想是让小的数据尽快往前,大的数据尽快往后
2、直接插入排序
完成预排序之后,整个序列就已经接近于有序了,再进行插入排序
gap代表有多少组
随着预排序的进行,会逐渐接近有序,后面挪动的就少了

预排序:
一组一组排序:先第一组,再控制gap躺
多组并排:直接++i,不用分组,直接对间隔为gap的两个数据之间进行插入排序,每一次都是一次数据有限的插入排序。理解清楚
先控制单趟,假设[0,end]是有序的,从end位置开始,从end+1往前进行对比排序,写完单趟,再对整体进行控制
控制单趟:对前end位置循环对比,这是一组;再对下一组进行比较。对gap分组的一整个数据组进行排序,这算作一趟
再整体:整个数组分成gap组,对每个gap组进行单趟排序
时间复杂度:
平均下来是O(n^1.3) (非常叼)
选择排序:
核心思想:
在整个序列选出最小值和最大值,最小值放在左边,最大值放在右边,然后依次再选出次小的和次大的。
先控制单趟,然后再整体控制,将区间往中间缩小
选择排序:遍历选择出最大的和最小的,然后将最大的放在后面,最小的放在前面;这就是单趟
然后,begin++,end--,缩小数组序列的间隔,因为最后的位置已经排序好了,因此缩小范围,在还未进行排序的序列组内继续进行上述的逻辑,挑出该组最大的和最小的进行操作。
但是注意有一个坑:例如,当最大的值在第一个位置,那么选出最小的值的时候就会将两者交换,但是下标没有变化,此时已经将最小的值交换到了第一个位置,然而maxi的位置依旧指向第一个位置,那么,此时选出最小值的操作已经结束,但是找到最大值的操作就会出现错误,因为此时maxi指向的第一个位置已经不是最大值了,而是变化最小值了,交换就会出现错误。
当此时再堆maxi进行交换,就会出现将第一个最小值和最后一个位置交换,结果导致,最小的在最后,最大的在某个位置,序列全乱,完全没有达到排序的效果
怎么解决这个问题?
很简单,进行一个if判断即可
maxi的值被改变,maxi的值应该是mini的位置,更新一下maxi = mini即可
因为交换第一个位置的时候,第一个位置是maxi,但是交换后,第一个位置已经被换成了min值,而最大值也被换到了mini的位置,所以此时最大值在mini的位置,此时更新一下maxi的位置即可
时间复杂度:
O(n^2)
因为无论是有序还是无序,无论交换与否都需要每次选出最大最小,所以,即使是有序时间复杂度依旧是O(n^2)
堆排序:
核心思想:
首先将数据进行建堆,然后将堆顶和最后的位置交换,再将堆顶向下调整。
向下调整建堆:倒着往上调整,而叶子节点是不需要向下调整的,所以调整位置从最后一个节点的父亲节点开始向上,逐个进行向下调整
我们的数据序列在物理结构上是一个数组,逻辑上是一个二叉树,从最后一个节点的父亲节点开始,依次向前,对数组的每一个数据进行向下调整,这样就保证了每一个节点都进行了向下调整建堆
因此,比较重要的是向下调整的逻辑:
从堆顶开始,和左右孩子进行比较,假设法,首先假设左孩子是符合条件的值,再对左后孩子的值进行比较,选出合适的孩子值,这是一个比较,子节点和父亲节点进行交换,再依次更新父节点和孩子节点,再考虑结束条件即可。当end为0时,执行向下调整,说明就剩下一个数据了,不需要进行调整了。
假设数组的大小为size,那么数组的下标范围是【0,size-1】
如果条件为<size,那么正好
时间复杂度:
O(NlogN)
快速排序:
霍尔版本:
核心思想:
找一个数据key,比key小的在左边,大的在右边,最后key的位置在序列的位置即定
例如说,左边有三个比key小的,那么key就在第四个位置
左边有4个比key小的,那么可以就在第五个位置
也就是说,当把所有比key小的放在左边,比key大的放在右边,那么最终即使是排好序的序列里,key的位置依旧是这个位置
那么,再把左右两边的序列变化有序的,那么整体就是有序的了
单趟:先选择第一个位置为key,然后在整体位置上,先找到右边比较小的值,再找到左边比较大的值,进行交换,再继续进行查找大小值
但是,有一个坑:即while(left < right)的判断条件不是if,l和R是动态变化着的,就有一种可能,即右边已经找到了比较小的值,然后左边开始从当前位置向前查找大的值,但是都没有,那么就会一直跑到right的右边
因为内部并没有判断,得完成了右边小值和左边大值的寻找结束才会进行判断,此时,right在左边,left在右边,再交换,就出错了。所以,在内部就需要多进行一个判断,即left < right
当进行第一次key排序好位置之后,要对key的左边和右边进行处理
怎么处理?
类似一个二叉树的递归过程
根(key)、左子树(区间)、右子树(右区间)
先对左边的区间同上一样的处理,只是此时的区间变成了【begin,keyi - 1】,对该区间进行key排序
再对右边的区间同上一样的处理,只是此时的区间变成了【keyi + 1, end】,对该区间进行key排序
什么时候条件结束?
当左子树或者右子树只有一个节点,即只剩下一个数据的时候,说明已经递归到最底层了
即,begin == end
但是,还有一个坑:就是当右边遇到一个和key相等的值会停止,左边也遇到一个和key相等的值也会停止,二者进行交换,交换过后;再继续下一个循环,可是,当前位置的right指向的是从左边left换过的key值,
当前位置的left指向的也是刚刚right交换过来的key值;那么再进行循环,还是会停止再当前的位置,两个位置循环交换,循环找,循环停,陷入死循环。
为什么会出现这样的情况?
因为,小的放在左边,大的放在右边
但是,相等的放在哪里?
似乎我们没有进行特殊的处理,仅仅只是对大的和小的进行了处理
因此,我们需要将相等的值也考虑进去
相等的值,放在左边和右边,都无关紧要。
因此,在右边找小值的时候,遇到和key相等的值,不管,继续往左边
同样,在左边找到大值得时候,遇到和key相等得值,不管,继续往右边
还有一个坑:当有序的情况下,其实开始位置用begin+1是有问题的,因为是有序的,右边的right往左边找小值,因为有序所以会一直往左边找,直到遇到left,但是我们初始的位置是begin+1位置
那么就会在begin+1的位置相遇,就会导致begin和begin+1位置进行交换,但是我们的数据本身就是有序的,结果你交换了,反倒打乱了顺序,不符合预期,所以初始位置要从begi位置开始
从begin位置开始,就可以避免这种情况,因为相遇的位置就是key位置本身,自己和自己交换,不影响序列的有序性
但是在有序的情况下,快排的效率是非常低的。因为我们选定key,例如一个有序序列,key是从第一个位置依次往后,那么就会导致,右边的right找小,一直都找不到,需要从头到尾遍历一遍,相当于一个冒泡了
相反,如果我们每次选择的key是一个中间值,那么整体的效率就会变得高效的多,时间复杂度是N*logN,因为类似于二叉树,n个数据有logN层,每一层有n个。
那怎么解决这个问题呢?
导致这个问题的根节点在于,选定第一个位置作为key
那么,我们只需要改变这个key即可
那么是不是意味着我们要将整个的单趟操作重写一遍呢?
不用
我们只需要将比较合适的数据和第一个位置的key进行交换即可,这样就不需要重写单趟逻辑
而且,这样的写法,本质上只是将key换成了一个更合适的值而已,其他都没有变
那么问题来了:怎么选择一个合适的key值呢?
第一种方法:从数据中随机选一个值
第二种方法:三数取中,即第一个、最后一个、中间值,取中间值。逻辑是,选择不是最大的,也不是最小的值做key,可以做到近似二分,效率更高。
为什么相遇左边一定比右边的大?:因为只有两种情况
1、R遇L
为什么相遇位置一定比key小?因为右边先走,当left找到大的,right找到小的,交换位置,交换位置后此时left的值是比key小的,而right是比key大的,此时继续再剩下的序列中ringht寻找比key小的值,直到相遇,将key和相遇位置交换,此时是right动,而在最后的一个过程中,一定是right往左边寻找,此时没有找到比key小的,就会直接找下去直到遇见left位置,交换位置
2、L遇R
当right已经找到了一个比key小的值的时候,轮到左边的left找比key大的值,但是没有,就会和right相遇,即相遇位置依旧是比key小
以上两种相遇方式保证了不论是那种相遇位置值都比key要小,但是关键是right先走
Debug版本本质是往代码文件录入很多调试信息,因此单个栈帧会比较大(所以栈容易溢出)
Release版本优化很多,例如一些中间一些没必要的步骤优化了(速度更快,栈也更多)
快速排序小区间优化:
快速排序递归对于小区间的排序付出的代价是比较大的,我们可以在小区间使用插入排序对区间进行排序,这种方法叫小区间优化
为什么说代价比较大呢?
例如最后几层,有7个值,按照我们的递归写法,我么需要建立几个函数栈帧?

7个函数栈帧,代价是比较大的。
而且如果是比较极端的情况,一个满二叉树,那么,最后几层的节点会非常的多,需要建立大量的函数栈帧,消耗代价是比较大的。
所以,考虑将这部分进行局部优化
快排类似于二叉树的遍历,而满二叉树的下面三层几乎占据整个数据序列的绝大多数,因此插入排序用于最后的3~4层的排序减少了很多递归
但是事实上,这个区间优化的效果并不是很明显,所以也不是很有必要,看你自己需求
上面我们说的是霍尔版本的快速排序,你会发现很麻烦,需要注意的点很多,稍不注意就会写错,所以我们有以下几个改进的方法:
快速单趟排序改进思路1:挖坑法
核心思想:在key位置首先挖一个坑,R往左边找,找到比key小的值,将该值填到key的位置,R所在位置为新的坑
那么什么叫做挖坑呢?就是把key的值记录下来,因为记录下来了,就可以进行覆盖,那么相当于key的位置就空出来了,形象的说,我们将之视为一个坑位。
而后L开始向右找比key大的值,找到后将该值放到右边R所在位置的坑,此时L所在位置又成为一个新的坑,如此反复,最后在而这相遇的位置将key填入,一趟快速排序完成,就保证了key的左边都是比key小的,右边都是比key大的
对于该key值得单趟排序完成,接下来,再对左区间和右区间进行如上单趟排序即可,如此递归到结束。这就是挖坑法的所有逻辑。
快速单趟排序改进思路2:前后指针法
核心思想:依旧是将小的放在前面,大的放在后面(最推荐的写法)
单趟排序:
前指针perv,后指针cur,key是第一个位置的值,
首先cur向右边走,cur的目的在于找比key小的值,没找到,继续向右;
如果找到了,那么说明什么?
说明prev和cur之间的值都是比key大的值
然后,交换位置,把++prev 和 cur位置进行交换
此时,从视觉上看,就像推箱子,这个箱子就是比key大的值的区间
这个区间是【prev,cur】
区间的左边都比key小,右边都比key大
那么,当时cur走到最后的位置的时候,就是把大于key的值区间推到了最后
到此,将prev 和 key位置的值进行交换即可,整个单趟排序结束。
整体控制:
快速排序,只要把单趟写好了,剩下的就是控制整体的区间问题,整个很简单。
【begin,keyi - 1】keyi 【keyi + 1, end】
然后进行递归,先左区间,再右区间
结束条件是当begin >= cur
为什么结束条件是这个呢?
因为,当左边只有一个值时,begin == keyi
当右边没有值时,右边的end就是keyii,keyi + 1 > keyi

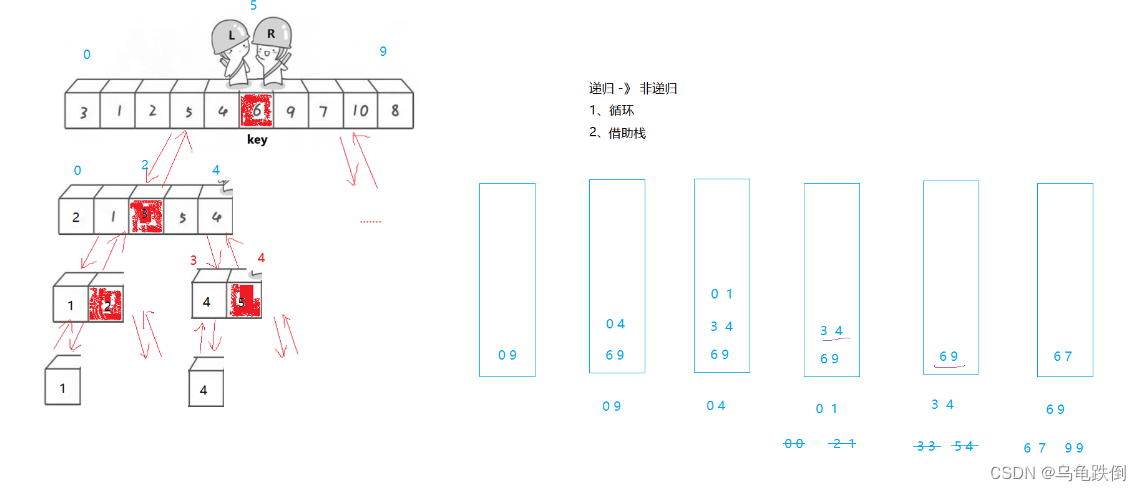
非递归快速排序:
递归改非递归:借助栈
事实上,因为有了三数取中,就可以使得递归的深度大大降低,就可以没有必要再写一个非递归的快排。
但是,我们不能保证,有些时候,递归的深度实在是太深了,那么递归的方式就行不通,所以,还是要掌握非递归
那么,非递归要怎么处理呢?
很简单,用一个栈来处理
因为本质上对于快速排序来说,单趟的逻辑都是一样的,唯一的区别就是要处理其区间的值
由于,单趟排序的性质,会形成左区间、key、右区间的形式
所以,非常类似于二叉树的结构,非常适合用递归
而递归,本质上也是对keyi的值,也就是区间进行处理
例如说,每一个递归函数,是建立一个栈帧,在这个函数栈帧里面,单趟逻辑是一样的
但是,只是从上一层传进来的数据的区间不一样
先递归左区间,是处理左区间
再递归右区间,是处理右区间
一样的道理
用非递归,我们只要控制好这个区间的值就可以了。
所以,使用栈是一个绝佳的方法
首先,begin、end入栈,对这个区间进行单趟处理,返回keyi值
begin、end出栈
再将该keyi的左区间和右区间进栈
再处理栈内记录的左区间,和有区间
如此循环,直到栈为空,结束排序
所有排序的源码:
头文件
#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include"Stack.h"
//插入排序
void InsertSort(int* a, int i);
//希尔排序
void ShellSort(int* a, int n);
//冒泡排序
void BUbbleSort(int *a ,int n);
// 选择排序
void SelectSort(int* a, int n);
// 堆排序
void AdjustDwon(int* a, int size, int parent);
void HeapSort(int* a, int n);
//快速排序
void QuickSort(int* a,int begin,int end);
//非递归快速排序
void QuickSortNoneR(int* a, int begin, int end);
实现文件:
#include"sort.h"
#include"Stack.h"
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
//插入排序
void InsertSort(int* a, int n)
{
//[0,end]该区间内是有序,将end+1的数据插入到前面的区间内
//再依次往后传递
//小心越界的问题
//数组最后的位置是n-1
//我们排序的范围是,end + 1
//要让end + 1是最后的位置n - 1
//那么,最后的范围要等于n - 2
for (int i = 0; i < n - 1; ++i)
{
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
//冒泡排序
void BUbbleSort(int* a, int n)
{
for (int i = 0;i<n;++i)
{
for (int j = 0; j< n - i - 1;++j)
{
if (a[j] > a[j + 1])
{
Swap(&a[j],&a[j+1]);
}
}
}
}
//希尔排序
void ShellSort(int* a, int n)
{
//预排序
//int gap = n;
//while (gap > 0)
//{
// gap /= 3 + 1;
// for (int i = 0; i < n - gap; i += gap)
// {
// int end = i;
// int tmp = a[end + gap];
// while (end >= 0)
// {
// if (tmp < a[end])
// {
// a[end + gap] = a[end];
// end -= gap;
// }
// else
// {
// break;
// }
// }
// a[end + gap] = tmp;
// }
//}
int gap = n;
while (gap > 1)
{
//这里的gap条件>1,当gap大于1的时候,会进入循环,此时,gap再进行处理,一定会变成1
//这就保证了最后一次执行的插入排序一定是gap=1
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; ++i)
{
//控制单趟
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
// 选择排序
void SelectSort(int* a, int n)
{
int begin = 0;
int end = n - 1;
int maxi = begin;
int mini = begin;
while (begin < end)
{
for (int i = begin; i < end; ++i)
{
if (a[i] > a[maxi])
{
maxi = i;
}
if (a[i] < a[mini])
{
mini = i;
}
Swap(&a[begin], &a[mini]);
if (a[mini] > a[maxi])
{
maxi = mini;
}
Swap(&a[end], &a[maxi]);
}
--end;
++begin;
}
}
// 堆排序(升序,建大堆)
void AdjustDwon(int* a, int size, int parent)
{
int child = parent * 2 + 1;
while (child < size)
{
if (child + 1 < size && a[child] < a[child + 1])//保证右孩子存在
{
child++;
}
if (a[parent] < a[child])
{
Swap(&a[parent], &a[child]);
parent = child;
child = parent * 2+ 1;
}
else
{
break;
}
}
}
void HeapSort(int* a, int n)
{
//向下建堆
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDwon(a,n,i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[0],&a[end]);
AdjustDwon(a, end, 0);
--end;
}
}
int GetMidi(int *a,int begin, int end)
{
int midi = (begin + end) / 2;
if (a[begin] > a[end])
{
if (a[end] > a[midi])
return end;
else if(a[midi] > a[end])
midi;
else
return begin;
}
else//a[end] < a[midi]
{
if (a[end] > a[midi])
return end;
else if (a[begin] > a[midi])
return midi;
else
return begin;
}
}
//快速排序:单趟排序-hore版本(增加区间优化)
int PartSort1(int* a, int begin, int end)
{
//区间优化
if (end - begin + 1 <= 10)
{
InsertSort(a + begin, end - begin + 1);
}
int midi = GetMidi(a, begin, end);
Swap(&a[begin], &a[midi]);
int keyi = begin;
int left = begin;
int right = end;
while (left < right)
{
while (left < right && a[right] >= a[keyi])
{
--right;
}
while (left < right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
keyi = left;
return keyi;
}
//快速排序:单趟排序-挖坑法
int PartSort2(int* a, int begin, int end)
{
int midi = GetMidi(a, begin, end);
Swap(&a[begin], &a[midi]);
int key = a[begin];
int left = begin;
int right = end;
while (left < right)
{
while (left < right && a[right] > key)
{
--right;
}
Swap(&a[left],&a[right]);
while (left < right && a[left] < key)
{
++left;
}
Swap(&a[left], &a[right]);
}
a[left] = key;
return left;
}
//快速排序:单趟排序-前后指针法
int PartSort3(int* a, int begin, int end)
{
int midi = GetMidi(a, begin, end);
Swap(&a[begin], &a[midi]);
int keyi = begin;
int prev = begin;
int cur = prev + 1;
初始版本,逻辑上比较好理解
//while (cur <= end)
//{
// if (a[cur] > a[keyi])
// {
// ++cur;
// }
// else
// {
// if (++prev != cur)
// {
// Swap(&a[prev], &a[cur]);
// }
// ++cur;
// }
//}
//简洁版本
while (cur <= end)
{
if (a[cur] < a[keyi] && ++prev != cur)
Swap(&a[prev],&a[cur]);
++cur;
}
Swap(&a[keyi],&a[prev]);
return prev;
}
//快速排序
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return;
int keyi = PartSort3(a, begin, end);
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
//非递归实现快速排序
void QuickSortNoneR(int* a, int begin, int end)
{
Stack st;
StackInit(&st);
StackPush(&st, begin);
StackPush(&st, end);
//一定要注意栈的进栈和出栈的规律
while (!StackEmpty(&st))
{
int right = StackTop(&st);
StackPop(&st);
int left = StackTop(&st);
StackPop(&st);
int keyi = PartSort3(a, left, right);
//[left , keyi - 1] keyi [keyi + 1, right]
if(left < keyi - 1)
{
StackPush(&st, left);
StackPush(&st, keyi - 1);
}
if (keyi + 1 < right)
{
StackPush(&st, keyi + 1);
StackPush(&st, right);
}
}
StackDestroy(&st);
}
测试文件:
#include"sort.h"
#include"Stack.h"
void printArray(int* a,int n)
{
for (int i = 0; i< n;++i)
{
printf("%d ", a[i]);
}
printf("\n");
}
int a[] = { 9,8,7,6,5,4,3,2,1,0 };
void TestInsertSort()
{
printf("插入排序:");
InsertSort(a, sizeof(a) / sizeof(int));
printArray(a, sizeof(a) / sizeof(int));
}
void TestBUbbleSort()
{
printf("冒泡排序:");
BUbbleSort(a, sizeof(a) / sizeof(int));
printArray(a, sizeof(a) / sizeof(int));
}
void TestshellSort()
{
printf("希尔排序:");
ShellSort(a, sizeof(a) / sizeof(int));
printArray(a, sizeof(a) / sizeof(int));
}
void TestHeapSort()
{
printf("堆排序:");
HeapSort(a, sizeof(a) / sizeof(int));
printArray(a, sizeof(a) / sizeof(int));
}
void TestSelectSort()
{
printf("选择排序:");
HeapSort(a, sizeof(a) / sizeof(int));
printArray(a, sizeof(a) / sizeof(int));
}
void TestQuickSort()
{
printf("快速排序:");
QuickSort(a,0, sizeof(a) / sizeof(int) - 1);
printArray(a, sizeof(a) / sizeof(int));
}
void TestQuickSortNoneR()
{
printf("快速排序(非递归):");
QuickSortNoneR(a, 0, sizeof(a) / sizeof(int) - 1);
printArray(a, sizeof(a) / sizeof(int));
}
int main()
{
//TestInsertSort();
//TestBUbbleSort();
//TestshellSort();
TestHeapSort();
TestSelectSort();
//TestQuickSort();
//TestQuickSortNoneR();
return 0;
}



![[Android View] 可绘制形状 (Shape Xml)](https://img-blog.csdnimg.cn/direct/18beaa5600c14933ac0269b946d8701c.png)